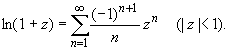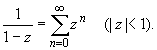Сформулируйте теорему о представлении ФКП степенным рядом и три следствия из неё. Нашла следствия только отдаленно похожие на лекции

Дайте определение интеграла от ФКП по кривой в С. Как его вычисление сводится к вычислению криволинейных интегралов второго рода?

Пусть на комплексной плоскости С задана ориентированная кусочно-гладкая кривая 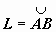, на которой определена функция w = f (z). Разобьём кривую точками z ₀ = A, z ₁, z ₂, …, z_n = B на n частей, на каждой из дуг 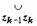выберем произвольную точку t_k, найдём f (t_k) и составим интегральную сумму 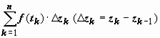. Предел последовательности этих сумм при n → ∞, max|Δ z _k| → 0 (k = 1, 2,..., n), если он существует, не зависит ни от способа разбиения кривой на дуги, ни от выбора точек t_k, называется интегралом от функции w = f (z) по кривой L и обозначается .

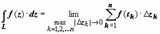Теорема. Если функция w = f (z) непрерывна на кривой L, то она интегрируема по этой кривой.
Док-во. Распишем действительные и мнимые части всех величин, входящих в интеграл: z _k = x _k + iy _k, f (z) = u (x, y) + iv (x, y), t _k = ξ _k + i ζ _k, Δ z_k = z_k − z_{k -1} = (x_k + iy_k) − (x_{k -1} + iy_{k -1}) = (x_k − x_{k -1}) + i (y_k − y_{k -1}) = Δ x _k + i Δ y _k, тогда f (t _k)·Δ z _k = (u (ξ _k, ζ _k) + iv (ξ _k, ζ _k))(Δ x_k + i Δ y_k) = (u (ξ _k, ζ _kk )·Δ x _k − v (ξ _k, ζ _k)·Δ y _k) + i (u (ξ _k, ζ _k)·Δ y _k + v (ξ _k, ζ _k)·Δ x _k), и сумма 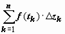разобьётся на две 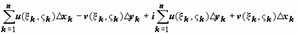. Каждая из этих сумм - интегральная сумма для действительных криволинейных интегралов второго рода, соответственно, 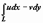и 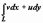. Если L - кусочно-гладкая кривая, w = f (z) - непрерывна (тогда непрерывны её координатные функции u (x, y) и v (x, y)), то существуют пределы этих сумм при max|Δ z_k | → 0 (k = 1, 2, 3,..., n) - соответствующие криволинейные интегралы, следовательно, существует 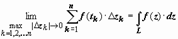, и .

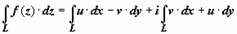Сформулируйте свойства интеграла от ФКП.

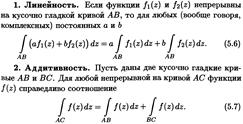
3. Продемонстрируйте вычисление интеграла на примерах функций f(z)=1, f(z)=z.

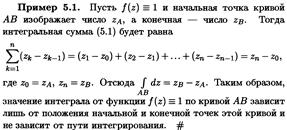
Сформулируйте интегральную теорему Коши для треугольника, произвольной односвязной области многосвязной области.

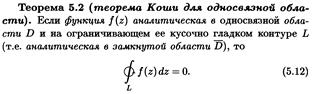
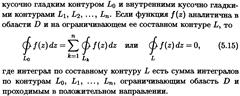
Для треугольника????????

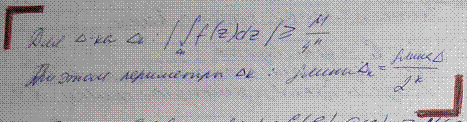
Как определяется функция F(z) с помощью интеграла с переменным верхним пределом? Какими свойствами она обладает? Сформулируйте теорему Ньютона-Лейбница.

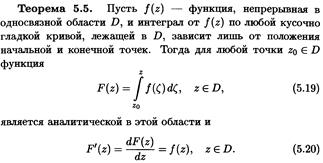
ИЛИ

Первообразная аналитической функции. Если функция w = f (z) аналитична в односвязной области D, то, как мы доказали, интеграл по кривой 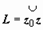зависит только от начальной и конечной точек и не зависти от формы кривой. Если зафиксировать начальную точку z ₀, то интеграл будет зависеть только от конечной точки z, поэтому можно написать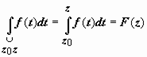

А В УЧЕБНИКЕ(И НЕ ТОЛЬКО В НЕМ) НЕ ТЕОРЕМА, А ФОРМУЛА НЬЮТОНА_ЛЕЙБНИЦА

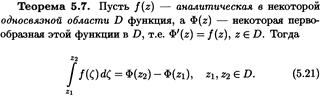
Сформулируйте интегральную теорему Коши. Что можно сказать о значении интеграла в этой теореме в случае, когда точка z0 не принадлежит G?

Я думаю, он имел в виду интегральную формулу Коши, теоремы же уже были выше…

Вместо G тут D

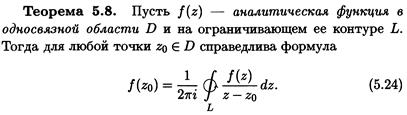
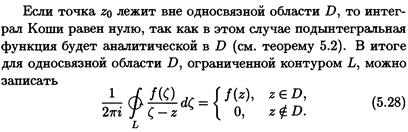
Сформулируйте свойства степенного ряда в комплексной плоскости. Как определить область сходимости такого ряда?

В лекциях так

Что ещё есть

Пусть дан степенной ряд a0+a1z+a2z2+…+anzn+…, где z=x+iy, а коэффициенты

a0, a1,…, an,…- комплексные или действительные числа.

Установлены следующие свойства:

1. Для каждого степенного ряда, вообще говоря, существует такое число R>0, что для

всех |z|<R степенной ряд сходится, для |z|>R – расходится. Точки z=x+iy

комплескной плоскости, для которых |z|<R, лежат внутри круга радиуса R с

центром в начале координат. Этот круг называется кругом сходимости степенного

ряда, а R – радиусом сходимости. Вне круга сходимости, то есть в точках, где |z|

>R, степенной ряд расходится. На границе круга, где |z|=R может иметь место

сходимость или расходимость.

Замечание. Если степенной ряд сходится только в точке z=0, то его радиус сходимости

полагают равным нулю: R=0. Если степенной ряд сходится при всех значениях z, то есть

во всей плоскости комплексного переменного, то радиус сходимости полагают равным

бесконечности: R=¥.

2. Внутри круга сходимости степенной ряд обладает всеми свойствами, которыми

обладают степенные ряды с действительными членами, то есть внутри круга

сходимости степенной ряд абсолютно сходится и его сумма S(z) есть непрерывная

функция комплексного переменного; степенной ряд внутри круга сходимости

можно почленно дифференцировать, причем полученный ряд имеет тот же радиус

сходимости, что и первоначальный.

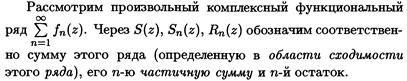
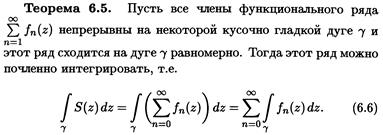
Сформулируйте теорему о представлении ФКП степенным рядом и три следствия из неё. Нашла следствия только отдаленно похожие на лекции

Теорема Тейлора (о разложении функции в степенной ряд).

Функция, аналитическая в области комплексных чисел D, в окрестности каждой точки z ₀ этой области представляется в виде степенного ряда:
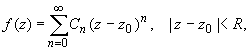(1)

радиус сходимости R которого не меньше, чем расстояние от точки z ₀ до границы области D.
Такой степенной ряд называется рядом Тейлора.

Коэффициенты ряда Тейлора вычисляются по формуле:

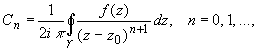(2)

где 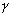- произвольный контур, принадлежащий области D и охватывающий точку z ₀ (в частности, 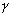- окружность 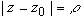), или по формуле:

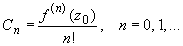(3)

Радиус сходимости ряда Тейлора равен расстоянию от точки z ₀ до ближайшей особой точки функции.

Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы:

 

 

 

 

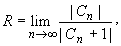
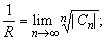
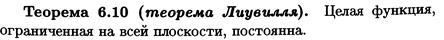
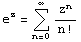(z принадлежит области комплексных чисел);

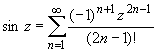(z принадлежит области комплексных чисел);

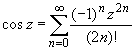(z принадлежит области комплексных чисел);

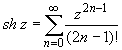(z принадлежит области комплексных чисел);

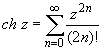(z принадлежит области комплексных чисел);