Билет №1
1. Смежные углы (определение). Теорема о сумме смежных углов.
2. Свойства параллелограмма. (Первое с доказательством)
Билет №2
1. Свойства равнобедренного треугольника (доказательство одного из них).
2. Свойства параллелограмм (Второе с доказательством)
Билет № 3
1. Теорема о сумме острых углов в прямоугольном треугольнике.
2. Признаки параллелограмма (Один с доказательством)
Билет № 4
1. Теорема о свойстве катета, лежащего против угла в 30º.
2. Теорема о биссектрисе угла
Билет № 5
1. Вертикальные углы (определение). Свойства вертикальных углов.
2. Теорема о серединном перпендикуляре к отрезку
Билет №6
1. Первый признак равенства треугольников.
2. Прямоугольник. Признак прямоугольника.
Билет № 7
1. Второй признак равенства треугольника.
2. Ромб. Свойство ромба.
Билет № 8
1. Третий признак равенства треугольника.
2. Квадрат. Основные свойства квадрата.
Билет № 9
1. Внешний угол треугольника (определение). Теорема о внешнем угле треугольника.
2. Теорема о вписанном угле
Билет № 10
1. Параллельные прямые (определение). Признаки параллельности двух прямых (доказательство одного из них).
2. Теорема о пересечении высот треугольника
Билет № 11
1. Треугольник (определение). Теорема о сумме углов треугольника.
2. Площадь прямоугольника.
Билет № 12
1. Построение треугольника по трём сторонам.
2. Площадь параллелограмма.
Билет № 13
1. Построение биссектрисы угла.
2. Площадь треугольника.
Билет № 14
1. Деление отрезка пополам.
2. Теорема об отношении площадей треугольников, имеющих по равному углу.
Билет № 15
1. Неравенство треугольника.
2. Площадь трапеции.
Билет № 16
1. Теорема о соотношении между сторонами и углами треугольника.
2. Теорема Пифагора
Билет № 17
1. Теорема об отрезках касательной.
2. Теорема, обратная теореме Пифагора.
Билет № 18
1. Построение угла, равному данному.
2. Теорема о свойстве касательной к окружности.
Билет № 19
1. Неравенство треугольника.
2. Отношение площадей подобных треугольников.
Билет № 20
1. Теорема о существовании и единственности перпендикуляра к прямой.
2. Первый признак подобия треугольников.
Билет № 21
1. Свойства равнобедренного треугольника. Одно с доказательством.
2. Второй признак подобия треугольников.
Билет № 22
1. Теоремы об углах, образованных двумя параллельными прямыми и секущей
2. Третий признак подобия треугольников.
Билет № 23
1. Свойства прямоугольного треугольника. Одно с доказательством.
2. Средняя линия треугольника.
Билет № 24
1. Теорема о внешнем угле треугольника.
2. Пропорциональные отрезки в прямоугольном треугольнике.
Билет № 25
1. Признаки равенства прямоугольных треугольников. Один с доказательством
2. Синус, косинус и тангенс острого угла прямоугольного треугольника.
| Задача № 1 Отрезки AC и BD пересекаются в точке О. AO=OC, BO=OD. При проведении отрезков AB и CD образуются треугольники BAO и OCD. Докажите, что ∆ BAO=∆ OCD. |
| Задача № 2 В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см. |
| Задача № 3 Один из вертикальных углов равен 45º. Найдите остальные углы. |
| Задача № 4 Один из внутренних накрест лежащих углов, образованных при пересечении двух параллельных прямых третьей прямой, равен 50º. Найдите градусные меры остальных углов. |
| Задача № 5 В треугольнике ABC AB=4 см, AC=6 см, BC=5 см. Какой угол треугольника наименьший, а какой наибольший? Почему? |
Задача № 6
В треугольнике ABC даны два угла:  =32º, =32º,  =57º. Найдите третий угол. =57º. Найдите третий угол.
|
| Задача № 7 Отрезок СЕ является медианой ACD. Известно, что AE=2,5 см, AC=3 см, CD=4 см. Найдите периметр треугольника ACD. |
| Задача № 8 Существует ли треугольник со сторонами 7 см, 2 см и 10 см? Ответ обоснуйте. |
Задача № 9
У треугольников ABC и DEK:  , AC=DK, AB=DE. Докажите, что , AC=DK, AB=DE. Докажите, что  . .
|
Задача № 10
Известно, что  =90º. Луч OD делит угол AOB на два угла: =90º. Луч OD делит угол AOB на два угла: 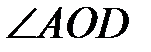 и и  . Найдите . Найдите  , если угол AOD в два раза меньше угла DOB. , если угол AOD в два раза меньше угла DOB.
|
Задача № 11
В треугольнике ABC  =90º, =90º,  =60º, AB=3,7 см. Найдите длину отрезка BC. =60º, AB=3,7 см. Найдите длину отрезка BC.
|
Задача № 12
В треугольнике ABC  =40º, внешний угол при вершине B равен 70º. Найдите остальные внутренние углы треугольника. =40º, внешний угол при вершине B равен 70º. Найдите остальные внутренние углы треугольника.
|
| Задача № 13 В треугольнике ABC AE – высота, BC- основание. Известно, что BC=12,8 см. Найдите длину отрезка CE. |
| Задача № 14 Найдите смежные углы, если один из них в два раза больше другого. |
| Задача № 15 В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см. |
| Задача № 16 Сумма данного угла и вертикального ему угла равна 60º. Найдите величину вертикального и смежных с ним углов. |
| Задача № 17 На отрезке OD, длина которого 24 см, отмечена точка A. Найдите длину отрезка AD, если отрезок OA на 8 см длиннее отрезка AD. |
| Задача № 18 Один из внешних углов прямоугольного треугольника равен 130º. Найдите острые углы треугольника. |
| Задача № 19 Периметр равностороннего треугольника DEK равен 18 см. Найдите стороны треугольника DEK. |
| Задача № 20 Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC. |
| Задача № 23 Боковая сторона равнобедренного треугольника в два раза больше его основания. Найдите стороны треугольника, если его периметр равен 20 см. |
| Задача № 21 Найдите смежные углы, если один из них в два раза больше другого. |
| Задача № 24 Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найти эти углы. |
| Задача № 22 Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника. |
| Задача № 25 Основание равнобедренного треугольника равно 8см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше периметра другого. Найти боковую сторону данного треугольника. |
| Задача № 26 В прямоугольном треугольнике ABC с прямым углом С внешний Угол при вершине А равен 120, АС+АВ=18см.Найти AC и AB. |
| Задача № 27 В треугольниках ABC и MKE отрезки СО и EH медианы, BC=KE, угол В равен углу К и угол С равен углу E. Доказать, что треугольник СО равен треугольнику MEH |
| Задача № 28 Внутри равнобедренного треугольника ABC с основанием ВС взята точка M такая, что угол MBC равен 30, угол MCB равен 10. Найти угол AMC, если угол ВАС равен 80. |
| Задача № 29 Отрезки AC и BM пересекаются и точкой пересечения делятся пополам. Доказать, что треугольник ABC равен треугольнику CMA. |
| Задача № 30 Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника |
ЗАДАЧИ К ЭКЗАМЕНУ ПО ГЕОМЕТРИИ ЗА 8 КЛАСС.