ПРАКТИКУМ
По теме «Тройной интеграл»
Задача о вычислении массы тела.
Имеем объем V заполненный массой с переменной плотностью f(x,y,z). Вычислим общую массу по всему объему методом интегральной суммы.
Опр. Тройным интегралом от функции трех переменных f(x,y,z) по объему V наз. предел интегральной суммы, полученной путем разбиения объема V на элементарные области D Vi с постоянной плотностью f (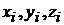 )
)
m = lim 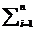 f (
f (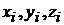 ) D Vi º
) D Vi º 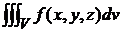 =
= 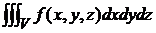 (1)
(1)
Физический смысл тройного интеграла – масса тела переменной плотности.
Вычисление тройных интегралов сводится к вычислению повторных интегралов при детальном учете конфигурации области интегрирования и зависит также от выбранной системы координат.
Прямоугольные координаты - x, y, z.
1. V - прямоугольный параллепипед (a 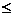 x
x 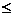 b, c
b, c 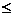 y
y 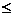 d, p
d, p 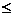 z
z 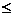 q), тогда
q), тогда
J = 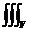 f(x,y,z) dx dy dz =
f(x,y,z) dx dy dz = 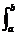 dx
dx 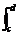 dy
dy 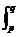 f(x,y,z) dz (2)
f(x,y,z) dz (2)
При вычислении внутренних интегралов оставшиеся переменныерассматриваются как константы. Возможен любой порядок интегрирования по х, у, z.
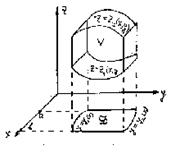 2. V - цилиндрический брус, который ограничен двумя гладкими поверхностями z = z1(x,y), z = z2(x,y) и его проекция на плоскость хОу образует правильную область D, например, a
2. V - цилиндрический брус, который ограничен двумя гладкими поверхностями z = z1(x,y), z = z2(x,y) и его проекция на плоскость хОу образует правильную область D, например, a 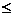 x
x 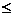 b, y1(x)
b, y1(x) 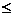 y
y 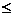 y2(x), тогда
y2(x), тогда
J = 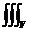 f(x,y,z)dx dy dz =
f(x,y,z)dx dy dz = 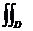 dxdy
dxdy 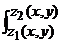 f(x,y,z) dz =
f(x,y,z) dz =
= 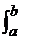 dx
dx 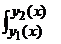 dy
dy 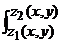 f(x,y,z) dz (3)
f(x,y,z) dz (3)
При f(x,y,z) = 1 интеграл определяет объем бруса.
Пример 1. Найти объем тела, ограниченного поверхностями:
z = 0, z = x2 + y2, y = x, y + x = 2, y = 0
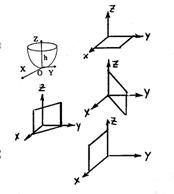 Решение.
Решение.
z = 0 (степень 1, нет y, z) 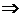 плоскость координатная xOy (низ)
плоскость координатная xOy (низ)
z = x2 + y2 (степени 1, 2)  параболоид вращения (верх)
параболоид вращения (верх)
y = x (степень 1, нет z)  плоскость через Oz (стенка)
плоскость через Oz (стенка)
y + x = 2 (степень 1, нет z)  плоскость || Oz (стенка)
плоскость || Oz (стенка)
y = 0 (степень 1, нет x, z)  плоскость координатная xOz (стенка)
плоскость координатная xOz (стенка)
V = 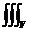 dx dy dz =
dx dy dz = 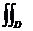 dxdy
dxdy 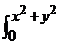 dz, J1 =
dz, J1 = 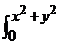 dz = x2 + y2
dz = x2 + y2
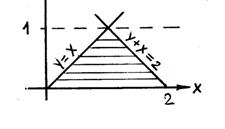
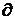 D: y = x, y + x = 2, y = 0
D: y = x, y + x = 2, y = 0
Точки пересечения линий
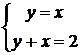
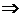 (1;1),
(1;1), 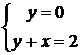
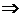 (2;0),
(2;0), 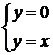
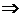 (0;0)
(0;0)
Построение рис. области D.
Выберем коридор || Оx, его ширина 0 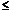 y
y 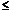 1,
1,
а движение по коридору от y = x до y + x = 2. D: 0 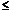 y
y 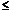 1, y
1, y 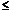 x
x 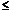 2 – y
2 – y
V = 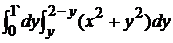 , J2 =
, J2 =  = [y2x + x3/3] |y2 – y =
= [y2x + x3/3] |y2 – y =
= 1/3 [ -7y3 + 12y2 – 12y + 8 ], V = 1/3 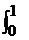 [-7y3 + 12y2 – 12y + 8] dy =
[-7y3 + 12y2 – 12y + 8] dy =
= 1/3 [-7y4/4 + 12y3/3 – 12y2/2 + 8y] |01 = 17/12 куб. ед.
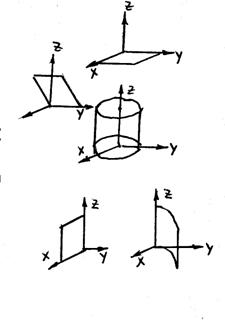 Пример 2. Найти объем тела, ограниченного поверхностями:
Пример 2. Найти объем тела, ограниченного поверхностями:
z = 10x, z = 0, x2 + y2 = 4, y = 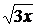 , y = 0
, y = 0
Решение.
z = 0 (степени1,нет y,x)  плоскость координатная xOy (низ)
плоскость координатная xOy (низ)
z = 10x (степени 1, нет у)  плоскость через Оу (верх)
плоскость через Оу (верх)
x2 + y2 = 4 (степени 2, нет z)  круговой цилиндр || Oz (стенка)
круговой цилиндр || Oz (стенка)
y = 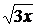 или у2 = 3х (степени 1, 2, нет z)
или у2 = 3х (степени 1, 2, нет z)  параболический цилиндр || Oz (стенка)
параболический цилиндр || Oz (стенка)
у = 0 (степени 1, нет х,z)  плоскость координатная zOх (стенка)
плоскость координатная zOх (стенка)
V = 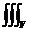 dx dy dz =
dx dy dz = 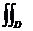 dxdy
dxdy 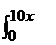 dz, J1 =
dz, J1 = 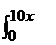 dz = 10x,
dz = 10x,
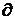 D: x2 + y2 = 4, у2 = 3х, у = 0
D: x2 + y2 = 4, у2 = 3х, у = 0
Точки пересечения линий
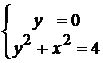
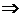 (2;0),
(2;0), 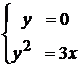
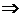 (0;0),
(0;0), 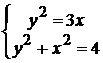
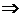 (1;
(1; 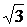 )
)
Построение рис. области D.
Выберем коридор || Оx, его ширина 0 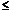 y
y 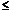
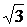 ,
,
а движение по коридору от у2 = 3х до x2 + y2 = 4,
D: 0 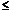 y
y 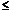
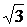 , y2/3
, y2/3 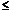 x
x 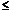
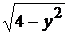
V = 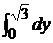
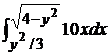 , J2 =
, J2 = 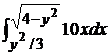 = 5 [ 4 – y2 – y4 /9 ],
= 5 [ 4 – y2 – y4 /9 ],
V = 5 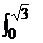 [ 4 – y2 – y4 /9 ] dy = 5 [ 4y – y3/3 – y5/45 ]
[ 4 – y2 – y4 /9 ] dy = 5 [ 4y – y3/3 – y5/45 ] 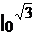 =
= 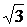 куб.ед.
куб.ед.
Задачи для самостоятельного решения
Найти объем тела, ограниченного поверхностями:
1) x + y + z = 8, y = x, z = 0, y = 3; 2) y = 6 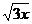 , y =
, y = 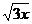 , z = 0, x + z = 3.
, z = 0, x + z = 3.
3) y = 6 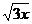 , y =
, y = 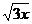 , z = 0, x + z = 3; 4) x2 + y2 = 8, x =
, z = 0, x + z = 3; 4) x2 + y2 = 8, x = 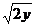 , x = 0, z = 30y/11, z = 0.
, x = 0, z = 30y/11, z = 0.
5) x + y = 4, x = 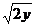 , z = 3x/5, z = 0; 6) x + y = 6, y =
, z = 3x/5, z = 0; 6) x + y = 6, y = 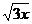 , z = 4y, z = 0.
, z = 4y, z = 0.
 Пример 3. Вычислить тройной интеграл
Пример 3. Вычислить тройной интеграл
J = 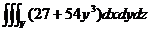 , где
, где 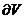 : y = x, y = 0, x = 1, z =
: y = x, y = 0, x = 1, z = 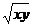 , z = 0.
, z = 0.
Решение.
y = x (степень 1, нет z)  плоскость через Oz (стенка)
плоскость через Oz (стенка)
у = 0 (степени 1, нет х, z) 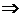 плоскость координатная zOх (стенка)
плоскость координатная zOх (стенка)
x = 1 (степень 1, нет y, z) 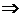 плоскость || yOz (стенка)
плоскость || yOz (стенка)
z = 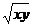 или z2 = xy (степень 2) сечения x = const, y = const – параболы (верх)
или z2 = xy (степень 2) сечения x = const, y = const – параболы (верх)
z = 0 (степени 1, нет y, x) 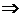 плоскость координатная xOy (низ)
плоскость координатная xOy (низ)
J = 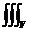 (27 + 54y3) dx dy dz =
(27 + 54y3) dx dy dz = 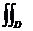 (27 + 54y3) dxdy
(27 + 54y3) dxdy 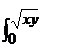 dz, J1 =
dz, J1 = 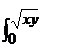 dz =
dz = 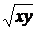
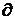 D: y = x, y = 0, x = 1
D: y = x, y = 0, x = 1
Точки пересечения линий
(0;0), (1;0), (1;1)
Построение рис. области D.
Выберем коридор || Оy, его ширина 0 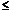 x
x 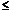 1,
1,
а движение по коридору от у = 0 до y = x D: 0 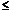 x
x 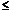 1, 0
1, 0 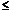 y
y 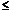 x
x
J = 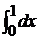
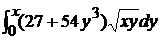 , J2 =
, J2 = 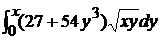 =
= 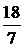 (7x2 + 6x4),
(7x2 + 6x4),
J = 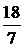
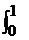 (7x2 + 6x4) dx =
(7x2 + 6x4) dx = 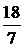 [ 7x3/3 + 6x5/5 ] |01 = 106/35
[ 7x3/3 + 6x5/5 ] |01 = 106/35
Задачи для самостоятельного решения
Вычислить тройной интеграл
1) J =  , где
, где 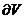 : y = 15x, y = 0, x = 1, z = xy, z = 0.
: y = 15x, y = 0, x = 1, z = xy, z = 0.
2) J = 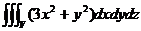 , где
, где 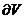 : z = 10y, x + y = 1, x = 0, y = 0, z = 0.
: z = 10y, x + y = 1, x = 0, y = 0, z = 0.
3) J = 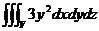 , где
, где 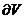 : y = 2x, y = 0, x = 2, z = xy, z = 0.
: y = 2x, y = 0, x = 2, z = xy, z = 0.
4) J = 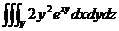 , где
, где 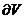 : x = 0, y = 1, y = x, z = 0, z = 1.
: x = 0, y = 1, y = x, z = 0, z = 1.
5) J =  , где
, где 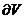 : x + y + z = 1, x ³ 0, y ³ 0, z ³ 0.
: x + y + z = 1, x ³ 0, y ³ 0, z ³ 0.
6) J = 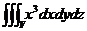 , где
, где 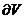 : x = 0, y = 0, y = 2, z = 2, z = x2.
: x = 0, y = 0, y = 2, z = 2, z = x2.
7) J = 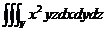 , где
, где 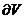 : y = 4, z = 4 – x2.
: y = 4, z = 4 – x2.
8) J = 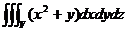 , где
, где 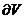 : x + y + z = 2, x + y – z = 0, x = 0, y = 0.
: x + y + z = 2, x + y – z = 0, x = 0, y = 0.