Центробежная сила.
(Митькин Александр Ильич)
Что такое центробежная сила и является ли она инерционной?
Часть 1. Рассмотрим движение тела вдоль произвольной плоской кривой.
На тело в любой точке траектории действует какая-то результирующая сила 
, которую можно разбить на две силы 
и 
. Одна из них действует вдоль касательной к траектории в данной точке, другая перпендикулярна этой касательной.
Понятно, что сила , действующая вдоль касательной не может изменить траектория, она лишь изменяет величину скорости тела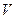 
. Сила же , направленная перпендикулярно касательной, изменяет траекторию. Именно она её заворачивает в свою сторону. Мы её называем центростремительной.
Сила может быть порождена разными явлениями: это может быть гравитация, реакция дороги или что-то ещё.
Хорошо, теперь давайте уберём из рассмотрения дорогу или иные посторонние предметы и оставим только силы, действующие на тело, т.е. вернёмся к рисунку 1, где изображены траектория, тело и силы, действующие на тело.
Введём мгновенную систему координат, связанную с нашим телом. Оси координат направим вдоль касательной и перпендикулярно ей. Относительно исходной системы, введённая система считается неподвижной. Т.е. её начало координат совпадает с местоположением тела, скорость тела в ней равна 
, силы и по модулю не изменились. В этой системе векторы уже не рассматриваются, т.к. силы и скорость, получается, всегда имеют направление вдоль координатных осей.
Ок. Давайте начнём перемещать вдоль траектории и составим в для каждой точки уравнение для сил. Что у нас получится? – а получится у нас то, что под действием силы у нас должна была бы появиться скорость направленная перпендикулярно траектории. Однако, поскольку мы с траектории не сходим, то, значит, эта скорость равна нулю. Это противоречие можно разрешить только одним способом, если мы введём силу 
, равную по модулю силе , но противоположно ей направленная. Это сила называется центробежной.
Итак, центробежная сила появилась когда мы ввели мгновенная система координат. По величине она всегда равна центростремительной силе, но мы пока не в курсе как их считать.
Является ли введённая центробежная сила инерционной? – нет, т.к. систему координат мы ввели неинерционную, а мгновенную.
Рассмотрим отличия трёх систем координат: неподвижной, инерционной и мгновенной.
А) Пусть тело движется равномерно и прямолинейно со скоростью V в неподвижной системе координат. При этом меняется её координата.
В инерционной системе, связанной с телом, скорость тела будет равна нулю (т.к. начало координат инерционной системы движется со скоростью тела). Координата тела в этой системе также равна нулю.
В мгновенной системе координат, связанной с телом, координата тела равна нулю, но вот скорость нулю не равна, она равна той же скорости, что и в неподвижной системе координат, V.
Б) Рассмотрим, теперь пассажира, сидящего на кресле в автомобиле. Автомобиль, а значит и кресло начнём тормозить. Пусть для определённости автомобиль в неподвижной системе координат двигался вправо. Тогда, для того, чтобы его затормозить, мы должны приложить к автомобилю силу F, направленную влево.
В инерционной системе координат начало отсчёта свяжем с креслом автомобиля. Соответственно, в этой системе на кресло сила не действует, но пассажира по инерции тянет продолжить движение вправо. Т.е. на пассажира действует сила, равная по модулю силе F, но направленная по ходу движения (вправо).
В мгновенной системе координат начало отсчёта связано с сиденьем, но сиденье в этой системе начинает затормаживать движение. Т.е. в этой системе, как и в неподвижной, на сиденье (или автомобиль) действует сила, направленная влево.
Мы видим, что мгновенная система координат отличается от инерционной и от неподвижной. Если бы мы рассматривали движение по траектории в неподвижной системе координат, то повода вводить центробежную силу не было бы, это свойство мгновенной системы.
Часть 2. Любую траекторию можно разбить на бесконечно малые отрезки. В пределе такая ломанная линия стремиться линии траектории.
Вместо отрезков можно использовать части окружностей, с выпуклость, совпадающей с выпуклостью траектории в данном месте. В пределе такая траектория будет совпадать с исходной.
Таким образом, любой достаточно малый участок траектории может быть описан как движение по окружности. При движении по окружности мы знаем, как считается центробежная сила. Поскольку радиус определяется траекторией, то центробежная сила, это функция траектории и скорости.
Зная траекторию в данной точке и величину центростремительной силы в той же точке, мы однозначно определяем скорость в этой точке. Зная траекторию и скорость в данной точке (например, на трассе) мы однозначно определяем центростремительную силу, а значит, и реакцию опоры.
.