Циклические коды
Циклические коды являются разновидностью систематических кодов.
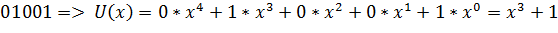
Пример. Сложить два полинома 
и 
(x^3+x^2+x)Å (x^3+x^2+x)
Результат: 
Пример. Умножить полином на полином
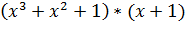
Результат:
.
Пример. Разделитьполином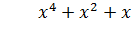 
на полином .
Результат: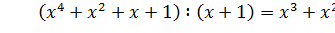 
Если комбинации 
, то циклический сдвиг так же приводят к разрешенной комбинации.
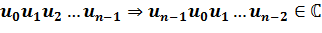
Циклическая перестановка соответствует умножению на 
.
1. 
2. 
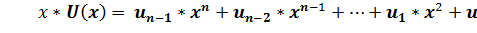
В первом члене нужно заменить 
на 1.
3. 
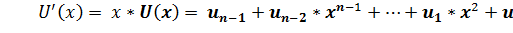
Полученный полином является циклическим сдвигом комбинации 
.
Принцип построения циклических кодов
Идея построения циклических кодов базируется на использовании неприводимых многочленов.
Определение. Неприводимым называется многочлен, который не может быть представленв виде произведения многочленов низших степеней, т. е такой многочлен делится толькона самого себя или на единицу и не делится ни на какойдругой многочлен.
На такой многочлен делится безостатка двучлен 
.
Неприводимые многочлены в теории циклических кодов играют роль образующих полиномов.
Чтобы понять принцип построения циклического кода, умножаем комбинацию простого 
кода 
на одночлен 
, азатем делим на образующий полином 
, степень которого равна . В результате умножения на степень каждого одночлена, входящего в , повышаетсяна k.
При делении произведения 
на образующий полином получается частное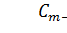 
такой же степени, как и .
Результат умножения и деления можно представить как
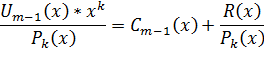
где 
– остаток от деления 
на .
Частное 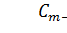имеет такую же степень‚ как и кодовая комбинация простого кода‚поэтому 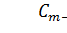является кодовой комбинацией этого же-простого 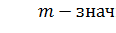кода.
Следует заметить, что степень остатка не может быть больше степени образующего полинома, т. е. его наивысшая степень может быть равна 
. Следовательно, наибольшее число разрядов остатка не превышает числа .
Пример. Дано 
и образующий полином третьей степени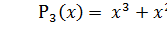 
. Следовательно, кодовые комбинации циклического кода будут иметь по семь разрядов. Требуется записать произвольную кодовую комбинацию циклического кода (7,4) первым способом. Возьмем произвольную четырех-разрядную комбинацию 
, то есть 
.
Найдем произведение
.
(0111 000)
Произведем деление:
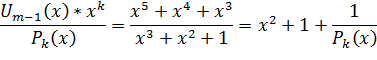
Следовательно, остаток 
.
Комбинация, принадлежащая циклическому (7,4) коду: 
или в двоичной форме: 
.
Схематично полученную комбинацию можно представить так:
Матричное представление циклических кодов
Образующая матрица размера (
).
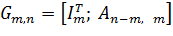
Образующая матрица даёт возможность получить первые 
комбинаций кода. Остальным 
комбинацией получает суммированием по модулю 2 строк мат.
Последняя комбинация является нулевой.
Пример. Дано 
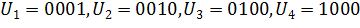
Произведем необходимые операции с векторами 
(
).
, следовательно первая строка 
После аналогичных операций с , , получаем 
.
Получим производящую матрицу в виде:
= 
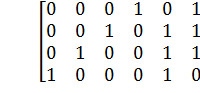
Дополнительную матрицу 
можно построить по остаткам от деления последней строки матрицы 
, дополненной нулями на обратный полином.
Строки матрицы 
являются четырьмя первыми комбинациями кода, пятая комбинация – нулевая, остальные – линейными комбинациями остальных четырех строк.