ПРИЛОЖЕНИЕ
Элементы комбинаторики
Комбинаторика – это наука о том, сколько различных комбинаций, удовлетворяющих определенным условиям, можно составить на элементах конечного множества.
Чтобы проводить комбинаторные рассуждения необходимо знать основные правила, схемы и формулы комбинаторики.
Пусть X – конечное множество, а 
– количество элементов в нем. Будем в этом случае говорить, что объект x из X может быть выбран n способами.
«Правило суммы»
Пусть 
, 
, …, 
– попарно непересекающиеся множества, т.е. 
при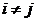 
. Тогда, очевидно, выполняется равенство
.
Этот факт в комбинаторике называется «правилом суммы».
«Правило произведения»
«Если объект x может быть выбран m способами и после каждого из таких выборов объект y в свою очередь может быть выбран n способами, то выбор упорядоченной пары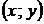 
может быть осуществлен mn способами».
Доказательство. Воспользуемся правилом суммы. Пусть 
– множество элементов, из которых выбирается объект x. Для каждого 
рассмотрим множества 
, в которых первая компонента совпадает с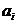 
. Множества 
попарно не пересекаются и 
. Тогда множество всех пар 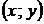есть 
и (по правилу суммы)
¢
Замечание. В общем случае правило произведения формулируется следующим образом: «Если объект 
может быть выбран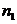 
способами, после чего объект 
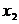может быть выбран 
способами и для любого i, где 
, после выбора объектов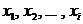 
объект 
может быть выбран 
способами, то выбор упорядоченной последовательности 
может быть осуществлен 
способами».
Доказательство проводится методом математической индукции.
Размещения и сочетания
Определение 1. Набор элементов 
, 
,…, 
из множества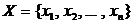 
называется выборкой объема r из n элементов (или, иначе, 
- выборкой).
Выборка называется упорядоченной, если порядок следования элементов в ней задан.
Замечание. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.
Если порядок следования элементов не является существенным, то выборка называется неупорядоченной.
В выборках могут допускаться или не допускаться повторения элементов.
Определение 2. Упорядоченная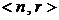 
-выборка, в которой элементы могут повторяться, называется 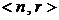- размещением с повторениями.
Определение 3. Упорядоченная 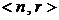-выборка, элементы которой попарно различны, называется 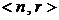- размещением без повторений (или, иначе, 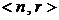- размещением).
Замечание. 
-размещения без повторений называются перестановками множества X.
Определение 4. Неупорядоченная 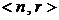-выборка, в которой элементы могут повторяться, называется - сочетанием с повторениями.
Определение 5. Неупорядоченная 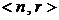-выборка элементы, которой попарно различны, называется 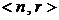- сочетанием без повторений (или, иначе, 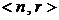- сочетанием).
Замечание. Любое -сочетание можно рассматривать, как r -элементное подмножество n -элементного множества.
Пример 1. Пусть 
, т.е. 
. Найти какое-либо 
-сочетание без повторений.
Ответ: например,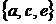 
.
Пример 2. Пусть 
. Найти все 
-размещения и -сочетания (с повторениями и без повторений).
Ответ:
а) 
– множество всех -размещений с повторениями (9 упорядоченных пар);
б)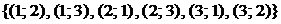 
– множество всех -размещений без повторений (6 упорядоченных пар);
в)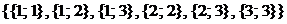 
– множество всех -сочетаний с повторениями (6 неупорядоченных пар);
г) 
– множество всех -сочетаний без повторений (3 неупорядоченные пары, являющиеся двухэлементными подмножествами трехэлементного множества).
Число 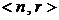-размещений с повторениями будем обозначать 
, а без повторений – через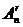 
. Число перестановок n -элементного множества будем обозначать через 
(т.е. 
). Число 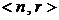-сочетаний с повторениями будем обозначать через 
, а без повторений – через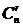 
.
Теорема 1. 
.
Доказательство. Каждое 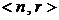-размещение с повторениями является упорядоченной последовательностью длины r, причем каждый элемент этой последовательности может быть выбран n способами. По правилу произведения получаем
¢
Теорема 2. 
.
Доказательство. Каждое 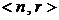-размещение без повторений является упорядоченной последовательностью длины r, члены которой попарно различны и выбираются из множества с n элементами. Тогда первый член этой последовательности может быть выбран n способами, после каждого выбора первого члена последовательности второй член может быть выбран 
способами и так далее до r -го члена последовательности, который может быть выбран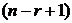 
способами. По правилу произведения получаем
¢
Следствие. 
Теорема 3. 
.
Доказательство. Каждое 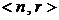-сочетание без повторений можно упорядочить r! способами. Объединение получаемых таким образом попарно непересекающихся множеств 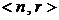-размещений без повторений для всевозможных 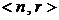-сочетаний без повторений, даст все 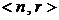-размещения без повторений. Тогда 
(здесь суммирование производится по всевозможным 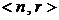-сочетаниям без повторений), т.е. 
. Отсюда
¢
Теорема 4. 
.
Доказательство. Каждому 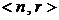-сочетанию В с повторениями, составленного из элементов множества 
поставим в соответствие такой вектор 
длины (
), состоящий из r единиц и (
)нулей, что число единиц находящихся между 
-м и i -м нулями, где 
, будет равно числу элементов 
, входящих в сочетание В. Число единиц, стоящих перед первым нулем равно числу элементов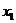 
, а число единиц, стоящих после -го нуля равно числу элементов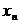 
, входящих в сочетание В.
Это соответствие между В и будет взаимно однозначным. Поэтому, чтобы подсчитать количество 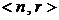-сочетаний с повторениями, достаточно подсчитать количество векторов .
Количество векторов равно числу r -элементных подмножеств (номеров единичных компонент в этих векторах) ()-элементного множества (всех номеров компонент в этих векторах), т.е. числу 
-сочетаний без повторений:
¢
Пример 3. Пусть 
, 
, 
, 
– 
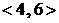-сочетание с повторениями, тогда 
.
Пример 4. Пусть , , , 
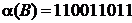, тогда 
.
Задачи
Правила комбинаторики
1. В меню столовой имеется 7 первых, 9 вторых и 4 третьих блюда. Сколькими способами можно выбрать обед из трех блюд (первое, второе и третье)?
Ответ: 
.
2. Допустим, что у вас есть 4 пары туфель, 3 брюк и 2 свитера. Каким числом способов вы можете одеться?
Ответ: 
.
3. На гору ведут 7 дорог. Сколькими способами турист может подняться на гору и спуститься с нее, если подъем и спуск должны осуществляться по разным дорогам?
Ответ: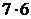 
.
4. Сколькими способами можно поставить на шахматную доску 2 ладьи (белую и черную) так, чтобы они не били друг друга?
Ответ: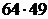 
.
Размещения и перестановки без повторений
1. Сколько слов длиной 4 можно составить, используя только 7 различных букв, если буквы в слове не повторяются?
Ответ: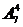 
.
2. В чемпионате участвует 16 команд. Сколькими способами могут быть распределены на финише 10 первых мест?
Ответ: 
.
3. Сколькими способами 4 юношей могут пригласить на танец 4 из 6 девушек?
Ответ: 
.
4. В чемпионате участвует 16 команд. Сколькими способами могут они быть распределены на финише турнира?
Ответ: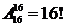 
.
5. Сколькими способами на шахматной доске можно расставить 8 одинаковых ладей так, чтобы они не били друг друга?
Ответ: 
.
6. Сколько существует таких перестановок чисел 1, 2, …, n, в которых число 1 стоит перед числом 2, причем числа 1 и 2 не обязательно соседние?
Ответ: 
.