ОТЧЕТ
О педагогической практике
в период с «1 » февраля 2013 г. по «2 » марта 2013 г.
в ТюмГУ, ИМЕНИТ
Выполнила магистрант II курса, гр. 25Мм 112М:
____________________________Чуракова М.Л.
Руководитель практики:
к.ф.-м.н., доцент
_____________________________Баринов В.А.
Тюмень – 2013
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ.. 4
ЛЕКЦИОННЫЕ ЗАНЯТИЯ.. 15
ЗАКЛЮЧЕНИЕ. 22
ВВЕДЕНИЕ
Педагогическая практика заключалась в проведении занятий по дисциплине «Уравнения в частных производных» (4 часа практических занятий 22.02.2013 г. и 4 часа лекций 01.03.2013 г.). Занятия проводились со студентами группы 301 3-го курса направления «Математика».
При подготовке к занятиям изучены лекции руководителя практики В.А. Баринова, а так же получены консультации для проведения практических занятий по представленным темам.
Для углубленного изучения излагаемых тем использованы следующие источники:
1. Баринов В.А. Лекции по уравнениям математической физики. Тюмень: ТюмГУ, кафедра матем. моделирования, 2012.
2. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.:Наука, 1972.
3. Михлин С.Г. Курс математической физики. – СПб.: «Лань», 2002.
4. Владимиров В.С., Жаринов В.В. Уравнения математической физики. – М.:ФИЗМАТЛИТ, 2000.
5. Смирнов М.М. Дифференциальные уравнения в частных производных. – М.:Наука, 1964.
6. Сборник задач по уравнениям математической физики./ Под ред. Владимирова В.С. – М.: ФИЗМАТЛИТ, 2001.
7. Смирнов М.М. Задачи по уравнениям математической физики. – М.: Наука, 1975, 128 с.
Каждое занятие было проанализировано с руководителем практики. Выявлялись недостатки, оптимизировалась структура занятия. Результаты анализа занятия учитывались при подготовке к следующим занятиям.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Практические занятия были проведены 22.02.2013 г. с 13-30 до 15-00 и с 15-10 до 16-40
На практических занятиях рассмотрено решение I-ой краевой задачи для однородного волнового уравнения методом Фурье.
Студенты охотно выходили к доске, решали, почти всё получалось. Некоторые выходили по нескольку раз. Самые активные студенты получили соответствующие баллы.
Задачи, которые рассмотрены на занятиях, решались у доски:
Задача 1.
 , , 
| (1.1) |
Граничные условия

| (1.2) |
Начальные условия

| (1.3) |
Решение:
Решение задачи будем искать в виде произведения двух функций, каждая из которых зависит от одной переменной
 . .
| (1.4) |
Подставим (1.4) в уравнение (1.1)
 . .
|
Поделим полученное уравнение на произведение 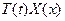 .
.
 . .
|
Левая часть этого равенства зависит только от  , а правая часть зависит только от
, а правая часть зависит только от 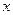 . Поэтому равенство возможно только если обе части равны одной и той же постоянной, т.е.
. Поэтому равенство возможно только если обе части равны одной и той же постоянной, т.е.
 , ,  , ,  . .
|
Можно показать, что при  решения краевой задачи не существует.
решения краевой задачи не существует.
В результате получаем систему уравнений
 . .
| (1.5) |
Решение (1.4) должно удовлетворять граничным условиям (1.2)
 или или  . .
|
Для определения функции  получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
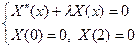 . .
|
Заметим, что задачу Штурма-Лиувилля можно поставить только для той функции, для которой получены нулевые граничные условия.
При  уравнение, входящее в систему, имеет решение
уравнение, входящее в систему, имеет решение
 , , 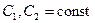 . .
|
Используем граничные условия. Из первого условия получаем, что  , тогда из второго следует
, тогда из второго следует 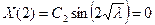 . В данном случае
. В данном случае  , иначе существует только тривиальное решение задачи, неудовлетворяющее граничным условиям, но тогда
, иначе существует только тривиальное решение задачи, неудовлетворяющее граничным условиям, но тогда  , откуда
, откуда  ,
, 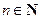 или
или
 . .
|
Следовательно,
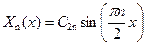 . .
|
Индекс «n» означает, что различным значениям n соответствуют различные решения.
Второе уравнение системы (1.5) при  имеет решение
имеет решение
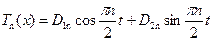 . .
|
Подставляя полученные  и
и  в (1.4), получаем
в (1.4), получаем
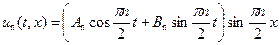 , ,
|
где  ,
,  .
.
В силу линейности уравнения (1.1) и граничных условий (1.2), сумма всех решений так же будет решением задачи, т.е.
 , ,
|
Коэффициенты 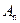 и
и 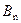 определяются из начальных условий
определяются из начальных условий

|
Разложим функции 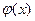 и
и 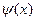 в ряд Фурье по
в ряд Фурье по 
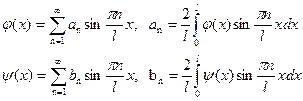
|
Тогда начальные условия примут вид

|
Сравнивая коэффициенты рядов, находим

|
Исходя из имеющихся начальных условий (1.3) функции 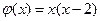 и
и  , тогда коэффициенты
, тогда коэффициенты 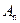 и
и 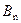

|
Вычислим определенный интеграл.
Распишем его для удобства на два интеграла. Вычислим каждый интеграл в отдельности.
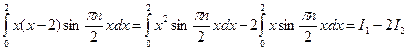

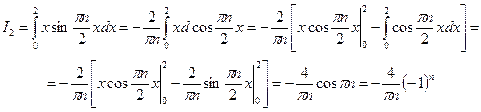

Т.о. решение данной задачи
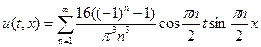 , ,
|
Задача 2.
 , , 
| (2.1) |
Граничные условия

| (2.2) |
Начальные условия

| (2.3) |
Решение:
Решение задачи будем искать в виде произведения двух функций, каждая из которых зависит от одной переменной
 . .
| (2.4) |
Подставим (2.4) в уравнение (2.1)
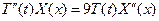 . .
|
Поделим полученное уравнение на произведение 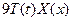 .
.
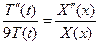 . .
|
Левая часть этого равенства зависит только от  , а правая часть зависит только от
, а правая часть зависит только от 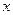 . Поэтому равенство возможно только если обе части равны одной и той же постоянной, т.е.
. Поэтому равенство возможно только если обе части равны одной и той же постоянной, т.е.
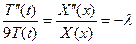 , ,  , ,  . .
|
Можно показать, что при  решения краевой задачи не существует.
решения краевой задачи не существует.
В результате получаем систему уравнений
 . .
| (2.5) |
Решение (1.4) должно удовлетворять граничным условиям (2.2)
 или или  . .
|
Для определения функции  получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
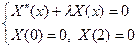 . .
|
При  уравнение, входящее в систему, имеет решение
уравнение, входящее в систему, имеет решение
 , , 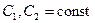 . .
|
Используем граничные условия. Из первого условия получаем, что  , тогда из второго следует
, тогда из второго следует  . В данном случае
. В данном случае  , иначе существует только тривиальное решение задачи, неудовлетворяющее граничным условиям, но тогда
, иначе существует только тривиальное решение задачи, неудовлетворяющее граничным условиям, но тогда  , откуда
, откуда 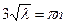 ,
, 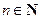 или
или
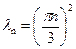 . .
|
Следовательно,
 . .
|
Индекс «n» означает, что различным значениям n соответствуют различные решения.
Второе уравнение системы (2.5) при 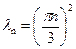 имеет решение
имеет решение
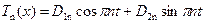 . .
|
Подставляя полученные  и
и  в (2.4), получаем
в (2.4), получаем
 , ,
|
где  ,
,  .
.
Общее решение уравнения (2.1), удовлетворяющее граничным условиям (2.2), имеет вид
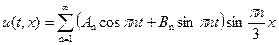 , ,
|
Коэффициенты 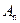 и
и 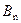 определяются из начальных условий
определяются из начальных условий
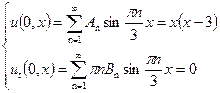
|
Из уравнений видно, что  . Разложим функцию
. Разложим функцию  в ряд Фурье по
в ряд Фурье по 

|
Сравнивая коэффициенты ряда, находим

|
Вычислим определенный интеграл.
Распишем его для удобства на два интеграла. Вычислим каждый интеграл в отдельности.

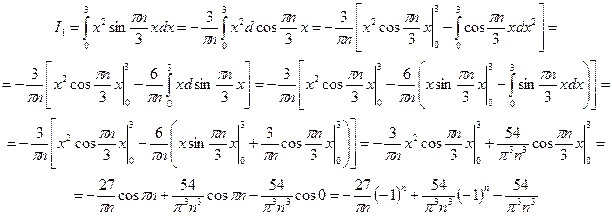

Подставим
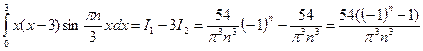
Т.о. решение данной задачи
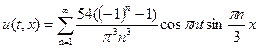 , ,
|
Задача 3.
 , , 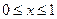
| (3.1) |
Граничные условия

| (3.2) |
Начальные условия

| (3.3) |
Решение:
Решение задачи будем искать в виде произведения двух функций
 . .
| (3.4) |
Подставим (3.4) в уравнение (3.1)
 . .
|
Поделим полученное уравнение на произведение 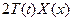 .
.
 . .
|
Левая часть этого равенства зависит только от  , а правая часть зависит только от
, а правая часть зависит только от 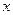 . Поэтому равенство возможно только если обе части равны одной и той же постоянной.
. Поэтому равенство возможно только если обе части равны одной и той же постоянной.
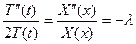 , ,  , ,  . .
|
В результате получаем систему уравнений
 . .
| (3.5) |
Решение (3.4) должно удовлетворять граничным условиям (3.2)
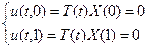 или или 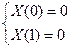 . .
|
Для определения функции  получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
 . .
|
При  уравнение, входящее в систему, имеет решение
уравнение, входящее в систему, имеет решение
 , , 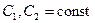 . .
|
Используем граничные условия. Из первого условия получаем, что  , тогда из второго следует
, тогда из второго следует 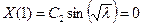 . В данном случае
. В данном случае  , иначе существует только тривиальное решение задачи, неудовлетворяющее граничным условиям, но тогда
, иначе существует только тривиальное решение задачи, неудовлетворяющее граничным условиям, но тогда 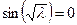 , откуда
, откуда  ,
, 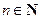 или
или
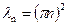 . .
|
Следовательно,
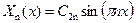 . .
|
Индекс «n» означает, что различным значениям n соответствуют различные решения.
Второе уравнение системы (3.5) при 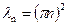 имеет решение
имеет решение
 . .
|
Подставляя полученные  и
и  в (3.4), получаем
в (3.4), получаем
 , ,
|
где  ,
,  .
.
В силу линейности уравнения (3.1) и граничных условий (3.2), сумма всех решений так же будет решением задачи, т.е.
 , ,
|
Коэффициенты 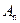 и
и 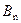 определяются из начальных условий
определяются из начальных условий

|
Из уравнений видно, что 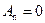 . Разложим функцию
. Разложим функцию  в ряд Фурье по
в ряд Фурье по 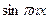

|
Сравнивая коэффициенты ряда, находим

|
Вычислим определенный интеграл.
Распишем его для удобства на два интеграла. Вычислим каждый интеграл в отдельности.
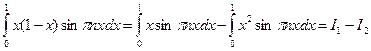

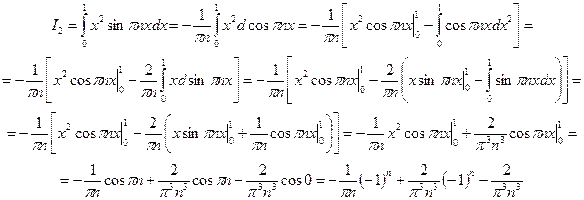

Т.о. решение данной задачи
 , ,
|
На пройденную тему было задано домашнее задание:
Задача 4.
 , , 
|
Граничные условия

|
Начальные условия

|
Задача 5.
 , , 
|
Граничные условия

|
Начальные условия

|
Задача 6.
 , , 
|
Граничные условия

|
Начальные условия

|
ЛЕКЦИОННЫЕ ЗАНЯТИЯ
Лекционные занятия проведены 01.03.2013 г.
На первой парах (с 13-30 до 15-00 и c 15-10 до 16-40) были рассмотрены две темы:
1. «Решение 1-ой краевой задачи для неоднородного волнового уравнения с однородными граничными условиями методом Фурье»;
2. «Решение общей 1-ой краевой задачи для волнового уравнения методом Фурье».
ЛЕКЦИОННЫЙ МАТЕРИАЛ
Решение задачи для неоднородного волнового уравнения
с однородными граничными условиями
Пусть задано неоднородное волновое уравнение:
 , ,  , , 
| (1) |
Граничные условия
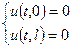
| (2) |
Начальные условия

| (3) |
где 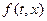 ,
,  ,
,  – заданные функции.
– заданные функции.
Если удается найти частное решение задач (1)-(3), то искомую функцию необходимо представить в виде:

|
где  – новая неизвестная функция, а
– новая неизвестная функция, а  – частное решение.
– частное решение.
В таком случае (1)-(3) перейдет в однородную задачу с ненулевыми начальными условиями для новой неизвестной функции  , и неоднородную задачу с нулевыми начальными условиями для функции
, и неоднородную задачу с нулевыми начальными условиями для функции  . Для функции
. Для функции  решение ищем в виде произведения двух функций, каждая из которых зависит от одной переменной. Для функции
решение ищем в виде произведения двух функций, каждая из которых зависит от одной переменной. Для функции  решение ищем в виде ряда по собственным функциям однородной задачи.
решение ищем в виде ряда по собственным функциям однородной задачи.
Случай 1.
Пусть правая часть уравнения (1) зависит только от 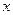 , т.о. она имеет вид
, т.о. она имеет вид  . В таком случае решение задачи будем искать в виде:
. В таком случае решение задачи будем искать в виде:

|
Подставим 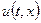 в (1):
в (1):

|
Функцию 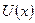 находим из краевой задачи:
находим из краевой задачи:
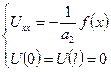
|
Из данного уравнения получаем:


|
Обозначим

|
Тогда из условий системы получаем:

|
Таким образом:

|
С учетом найденной функции 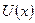 , для функции
, для функции  получим задачу вида:
получим задачу вида:
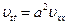 , ,  , , 
| |
 и и 
|
Полученная задача решается методом Фурье, рассмотренном на практическом занятии.
Случай 2.
Рассмотрим случай, когда частное решение подобрать не удается. Будем искать решение задач (1)-(3) в виде ряда по собственным функциям однородной задачи.

| (4) |
где 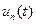 – неизвестная функция
– неизвестная функция
Чтобы получить уравнение для 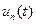 , разложим функции
, разложим функции  ,
,  ,
, 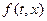 в ряд Фурье по собственным функциям однородной задачи:
в ряд Фурье по собственным функциям однородной задачи:
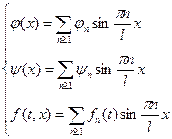
| (5) |

| (6) |
Подставим (4), (5) в уравнение (1), получим ряд:

|
Отсюда получаем уравнение для 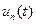 :
:

| (7) |
Для определения неизвестной 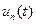 , получаем линейное неоднородное уравнение 2-огопорядка с постоянными коэффициентами.
, получаем линейное неоднородное уравнение 2-огопорядка с постоянными коэффициентами.
Решая уравнение (7) будем искать в виде:
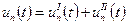
| (8) |
где  – частное решение неоднородного уравнения (7),
– частное решение неоднородного уравнения (7), 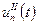 - общее решение однородного уравнения, соответствующего (7).
- общее решение однородного уравнения, соответствующего (7).
Решения  и
и 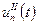 будем искать так, чтобы выполнялось условие:
будем искать так, чтобы выполнялось условие:

| |

|
То есть  – решение неоднородного уравнения с начальными неоднородными условиями,
– решение неоднородного уравнения с начальными неоднородными условиями, 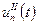 – решение однородного уравнения с неоднородными начальными условиями. Поэтому их сумма будет решением неоднородного уравнения с неоднородными начальными условиями.
– решение однородного уравнения с неоднородными начальными условиями. Поэтому их сумма будет решением неоднородного уравнения с неоднородными начальными условиями.

|
Найдем 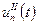
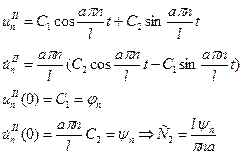
| |

| (9) |
Находим частное решение неоднородного уравнения с помощью метода неопределенных коэффициентов, решение ищем в виде:

| |
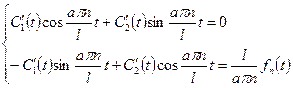
| |

| |

| |

|
Нашли решение системы Лагранжа:

| |
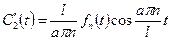
|
Найдем 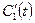 и
и  :
:

| |

|
Таким образом

| (10) |
Покажем, что функция (10) является решением неоднородного линейного уравнения с однородными начальными условиями. Для этого подставим в неоднородное уравнение сначала ряды (4), (5), а затем для функции  получим уравнение (7) и однородные начальные условия. Чтобы найти
получим уравнение (7) и однородные начальные условия. Чтобы найти  ,
, 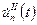 воспользуемся формулой Лагранжа:
воспользуемся формулой Лагранжа:
 формула Лагранжа: формула Лагранжа:
| |

|
Таким образом:

| |

| |

| |
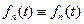
|
Значит решение (10) удовлетворяет неоднородному уравнению. Функция (10) и ее первая производная удовлетворяют однородным начальным условиям.
Если уравнение однородно, то получаем ранее решенную задачу. Решение  , домноженное на собственную функцию
, домноженное на собственную функцию  является решением этой задачи =>
является решением этой задачи =>  является решением однородного линейного уравнения с неоднородным начальным условием.
является решением однородного линейного уравнения с неоднородным начальным условием.
Тогда решение задачи (1)-(3), представленное формулой (4) примет вид:

| (11) |
Решение (11), записанное в виде суммы 2х рядов, имеет следующий физический смысл: 1‑й ряд описывает свободные колебания струны, 2‑й ряд описывает вынужденные колебания. За счет приложенной внешней силы с плотностью 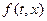 . 2-оеслагаемое в выражении (11) можно записать в виде:
. 2-оеслагаемое в выражении (11) можно записать в виде:

| (12) |

|
Эта функция называется функцией Грина, она описывает вынужденные колебания струны.