1. Исследуем систему с уравнением
2. 
на устойчивость.
Для этого перейдем от дифференциального уравнения к операторной форме.
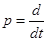- оператор дифференцирования, подставим его в данное уравнение.
Получаем характеристическое уравнение:
,
Находим корни квадратного уравнения:
D = b2 – 4 ac = T 12 – 4 T 2 = 0,7396 – 16,264 = –15,52;
α = –0,106.
Получили устойчивое состояние, т. к. αi < 0, т. е. все корни характеристического уравнения находятся в левой полуплоскости.
Проведем оценку качества системы.
а) Прямая оценка качества:
Находим передаточную функцию W(p):
Запишем переходную функцию.
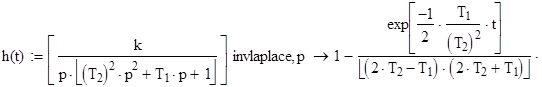
Построим график переходной функции h (t):
Учитывая, что с = 1,24, b = 1,068 мм2/с,
Находим время переходного процесса:
hуст = 1,
тогда Δ = 5%(hуст) = 0,05.
Определим перерегулирование – максимальное отклонение регулируемой величины от установившегося значения:
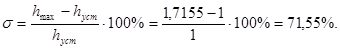
Находим колебательность системы, которое характеризуется числом колебаний регулируемой величины за время переходного процесса.
h = 3 (т. к. Четвертая волна не до конца).
Время нарастания регулируемой величины:
tн(tмах) = 13 с.
Время первого согласования, т.е. время, когда регулируемая величина первый раз достигает своего установившегося значения:
t1 = 7 с.
б) Косвенная оценка качества:
Рассмотрим амплитудно-частотную характеристику процесса.
Построим график амплитудно-частотной функции А (ω):
По графику проводим анализ:
1. Находим показатель колебательности – М.
, где Amax = 4,7545, A(0) = 1.
Следовательно М = 4,7545.
2. Резонансная частота ωр = 0,243, при Amax = 4,7545.
3. Частота среза при которой амплитудно-частотная характеристика достигает величины равной 1.
|
|
ωср = ± 0,3438.
Время переходного процесса и частота среза связаны соотношением:
tП ≈ (1÷2) 2π/ ωср ≈ (1÷2) 18,27 (с).
4. Полоса пропускания частот определяется:
Откладываем получившееся значение от Amax.
Получаем полосу пропускания:
ω1 = 0,2154 и ω1 = 0,2682.
3. Исследуем систему с уравнением
на устойчивость.
Для этого перейдем от дифференциального уравнения к операторной форме.
- оператор дифференцирования, подставим его в данное уравнение.
Получаем характеристическое уравнение:
,
Находим корни квадратного уравнения:
р = -1/Т1 = -1,163.
Получили устойчивое состояние, т. к. αi < 0, т. е. все корни характеристического уравнения находятся в левой полуплоскости.
Проведем оценку качества системы.
а) Прямая оценка качества:
Находим передаточную функцию W(p):
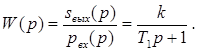
Запишем переходную функцию.
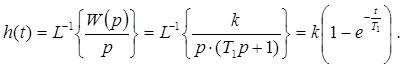
Построим график переходной функции h (t):
Так как система является устойчивой и график переходной функции не имеет колебаний, то можно определить только максимальное значение регулируемой величины, которое будет равно установившемуся:
hмах = hуст = 1.
Определим перерегулирование:
б) Косвенная оценка качества:
Рассмотрим амплитудно-частотную характеристику процесса.
Для этого находим частотную форму передаточной функции.
Построим график амплитудно-частотной функции А (ω):
По графику проводим анализ:
1. Находим показатель колебательности – М.
, где Amax = 1, A(0) = 1.
|
|
Следовательно М = 1.
2. Резонансная частота ωр = 0, при Amax = 1.
3. Частота среза при которой амплитудно-частотная характеристика достигает величины равной 1.
ωср = ± 0.
4. Полоса пропускания частот определяется:
.
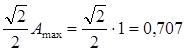Откладываем получившееся значение от Amax.
Получаем полосу пропускания:
ω = 1,155.
Вывод: после выбора и анализа элемента получили, что данный клапан можно применять как регулирующий клапан прямого действия (без дополнительных устройств) и как клапан непрямого действия (вводя дополнительные устройства управления). В первом случае на систему действуют инерционные силы, процесс регулирования становится более длительным и может быть неточным. При анализе элемента получили устойчивую систему, но процесс перерегулирования длится дольше, чем допустимое значение. Колебательность системы также выше приемлемого числа колебаний. Это говорит о том, что в процессе регулирования могут происходить сбои в работе, процесс становится нестабильным. Регуляторы прямого действияпросты в конструктивном отношении и надежны в эксплуатации, что объясняет их широкое применение для поддержания постоянного давления или перепада давлений воды на тепловых пунктах небольшой и средней мощности. Однако регуляторы прямого действия имеют меньшую чувствительность, поэтому рекомендуется применять при автоматизации объектов со сложными динамическими характеристиками регуляторы непрямого действия, так как они обеспечивают более широкий диапазон регулирования, возможность введения обратной связи и осуществление многоимпульсного регулирования. В нашем случае пневматический клапан применяется в системе с инерционным объектом, т. е. мы можем применять клапан, например с регулятором давления. Это позволяет получить устойчивую систему, как во втором случае.
|
|
Таблица 1 Характеристики материалов, применяемых для пружин
| Марка материала или класса проволоки | Диаметр d в мм | Механические свойства | Пределы температур, при которых могут работать пружины, в ˚С | Отличительные свойства материала | ||
| проволоки | прутка | Допускаемое напряжение при кручении τкр в кгс/мм2 | Модуль сдвига G в кгс/мм2 | |||
| П | 0,2 – 0,8 | – | 0,6 σв | от –40 до +120 | Высокие механические свойства | |
| В | 0,2 – 0,8 | – | 0,6 σв | » –40 » +120 | То же и устойчивая деформация | |
| 65Г | – | Свыше 5,0 | » –40 » +120 | Повышенная чувствитель-ность к перегревам и к образованию закалочных трещин | ||
| 60С2 | – | » 5,0 | » –40 » +250 | Повышенная склонность к обезуглероживанию пове-рхности при термооб-работке | ||
| 50ХФА | 0,5 – 14,0 | » 5,0 | » –40 » +400 | Устойчивая деформация | ||
| 4Х13 | 1,0 – 6,0 | » 5,0 | » –40 » +400 | Высокая коррозионная стойкость | ||
| 60С2Н2А | – | » 5,0 | » –40 » +250 | Повышенная склонность к обезуглероживанию пове-рхности при термооб-работке | ||
| Бр. КМц 3-1 | 0,3 – 10,0 | – | » –40 » +200 | Высокая коррозионная стойкость и антимаг-нитность | ||
| Бр. ОЦ 4-3 | 0,3 – 10,0 | – | » –40 » +200 | То же |
Таблица 2. Значение индекса пружины с пр (отношение среднего диаметра пружины к диаметру проволоки D: d) в зависимости от диаметра проволоки d
| d в мм | 0,2 – 0,4 | 0,45 – 1,0 | 1,1 – 2,2 | 2,5 – 6,0 | 7 – 16 | 18 – 40 |
| с пр = D / d | 8 – 14 | 6 – 12 | 5 – 10 | 4 – 10 | 4 – 8 | 4 – 6 |
Таблица 3. Значение коэффициента с в зависимости от определенного значения индекса пружины с пр
| с пр = D / d | |||||||
| с | 1,37 | 1,29 | 1,24 | 1,17 | 1,14 | 1,11 | 1,10 |
Список литературы
1. Гейер В.Г., Дулин В.С., Боруменский А.Г., Заря А.Н. Гидравлика и гидропривод. – М.: Недра, 1981. – 295 с.
2. Емельянов А.И., Емельянов В.А., Калинина С.А. Практические расчеты в автоматике. – М.: Машиностроение, 1967. – 316.
3. Ионин А.А., Хлыбов Б.М., Братенков В.Н., Терлецкая Е.Н. Теплоснабжение. – М.: Стройиздат, 1982. – 336 с.
4. Клюев А.С. Автоматическое регулирование. – М.: Энергия, 1973. – 392 с.
5. Смолянов Л.С. Инженерное оборудование коммунально-бытовых предприятий. – Киев: Будiвельник, 1978. – 256с.
6. Хакимов А.З., Абросимов В.Ф. Системы автоматизации технологических процессов. Расчет пневматических мембранно-пружинных исполнительных механизмов при проектировании. Руководящий материал. РМ4-179-80. Проектмонтажавтоматика, 1981. – 60 с.
7. Родов А.Б., Бунин А.Б., Бейгул Е.А., Курдыбал Б.М. Государственная система промышленных приборов и средств автоматизации. Номенклатурный каталог. Часть 2. – М.: Центральный научно-исследовательский институт информации и технико-экономических исследований приборостроения, средств автоматизации и систем управления, 1984. – 151с.
8. Устинова Е.И., Иванова О.И., Пайкин И.Х. Промышленная трубопроводная арматура. Каталог, часть III. – М.: Цинтихимнефтемаш, 1978. – 136 с.
9. ГОСТ 13373-67. Механизмы исполнительные пневматические мембранно-пружинные ГСП. Типы. Основные параметры и размеры. – Введ. 07.01.68. – М.: Издательство стандартов, 1967. – 12 с.