Уточнение корней нелинейного уравнения методом касательных

При уточнении корней методом касательных все функции делятся на два типа, как и в методе хорд. Рассмотрим кривую I-го типа.

Проведем касательную к графику функции в точке В. Она пересечет ось ОХ в точке х_{1 .} Через эту точку проведем прямую перпендикулярную оси ОХ до пересечения с графиком функции. Получим точку А₁. Через неё опять проведем касательную. Получим точку х₂. Продолжая этот процесс, получим последовательность х₁, х₂, х₃, …,х_{n ,} сходящуюся к х^*.

Уравнение касательной к графику функции f(x)=0 в точке х=b имеет вид . Т.к. эта касательная пересекает ось ОХ в точке (х₁, 0), то . Значит

Если, кривая относится ко II-му типу, то первую касательную к графику функции надо проводить в точке А и

Дальнейший расчет значений х₂, х₃, …,х_n не зависит от типа кривой и в обоих случаях вычисляется по формул.

Если на n-ом шаге , то считается, что необходимая точность е достигнута.

 

Уточнение корней нелинейного уравнения комбинированным методом

Методы хорд и касательных дают приближение корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом. В этом случае процесс уточнения корня идет быстрее.

Метод реализуется по следующей схеме:

1. По методу хорд находят первое приближение корня .

2. По методу касательных находят : .

3. По методу хорд: .

4. По методу касательных: .

Шаги 3 и 4 повторяются до тех пор, пока . Как только можно считать корень найденным .

 

Реализация в MathCad

 

Отделение корней нелинейного уравнения с использованием математической системы MathCad можно произвести графически или по приведённому выше вычислительному алгоритму.

 

Уточнение корней с помощью системы MathCad можно произвести методами:

- хорд;

- касательных;

- с использованием встроенных функций.

 

Метод хорд реализуется аналогично методу касательных.

4. Задание

 

4.1. Выполнить в среде Mathcad отделение корней уравнения f(x)=0 на [a, b] с шагом h=0,5

- по вычислительному алгоритму отделения корней;

- графическим методом.

4.2. Выполнить в среде Mathcad уточнение корней уравнения f(x)=0 на всех отрезках, полученных на этапе отделения корней с точностью 0,001

- методом хорд;

- методом касательных;

- используя встроенные функции Mathcad.

 

Номер варианта	Уравнение F(x)=0	Отрезок [a, b]
1.	cos(x)-x3=0	[-3, 2]
2.	x-10sin(x)=0	[2, 7]
3.	4x4-6,2-cos(2x)=0	[-3, 2]
4.	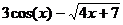=0	[0, 5]
5.	xsin(x)-1=0	[-2, 3]
6.	8cos(x)-x-6=0	[-5, 1]
7.	sin(x)-0,2x=0	[-2, 3]
8.	10cos(x)-0,1x2=0	[-2, 3]
9.		[-10,-5]
10.	3sin(2x)-2x3=0	[-2, 3]
11.	3sin(8x)-7x=0	[-1, 1]
12.	(x+5)2+6x+x4-13=0	[0, 5]
13.	3x-cos(x)-1=0	[-2, 6]
14.	-x/2=0	[-4, 5]
15.	ex-x-1=0	[-1, 3]
16.	5x-8Ln(x)=-8	[1, 5]

Тест. Найти все корни уравнения x⁴-x³-2x²+3x-3=0 на .

На этапе отделения корней с шагом h=1 получаем отрезки ,

Корни уравнения с точностью е=0,01: -1,73… и 1,73…

Порядок выполнения работы

5.1. Изучить теоретические сведения, необходимые для выполнения заданий.

5.2. Написать текст программы в среде MathCad. Выполнить расчёты, исправить ошибки при их обнаружении.

5.3. Выполнить тестовые задания.

5.4. Выполнить задания, соответствующие вашему варианту (по номеру компьютера).

5.5. Сохранить программу в своей папке.

5.6. Выполнить отчет о работе в письменном виде на листах формата А4.

5.7. Подготовить ответы на контрольные вопросы.