Комплексные числа и операции над ними
Для решения алгебраических уравнений множества действительных чисел R недостаточно (например, уравнения 
и 
не имеют действительных корней). Для преодоления указанного затруднения вводят множество комплексных чисел C (
). Решение уравнения обозначается через i и называется мнимой единицей, таким образом 
, 
. Уравнение имеет два комплексных корня 
.
Пример 1. 1) Решите уравнение 
.
Решение. Находим дискриминант и корни уравнения 
, 
.
2) Решите уравнение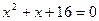 
.
Решение. Находим дискриминант и корни уравнения 
, 
.
3) Решите уравнение 
.
Решение. 
, 
4) Решите уравнение 
.
Решение. 
, 
или 
. Тогда 
, 
.
5) Решите уравнение 
.
Решение. 
, 
или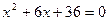 
. Тогда находим корни квадратного уравнения 
, 
.
Определение 1. Комплексным числом называется выражени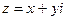е 
, где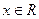 
, 
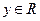, i – символ мнимой единицы. Число x называется действительной частью, а число y - мнимой частью комплексного числа 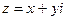. Два комплексных числа 
и 
, отличающиеся только знаком мнимой части, называются сопряжёнными.
Для комплексных чисел вводятся понятия равенства и операции сложения, вычитания, умножения и деления:
1) два комплексных числа 
и 
равны тогда и только тогда, когда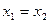 
, 
;
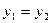2) комплексное число равно нулю 
тогда и только тогда, когда x= 0, y= 0;
3) суммой (разностью) чисел и называется число 
(в случае разности 
);
4) произведением чисел и называется число 
;
5) деление комплексных чисел определяется как действие, обратное умножению: если 
, где 
, 
, то x и y должны быть такими, чтобы выполнялось равенство 
.
Пример 2. Даны комплексные числа 
, 
. Найдите их сумму и разность.
Решение. 
, 
.
Пример 3. Даны комплексные числа 
, 
. Найдите их произведение и частное.
Решение.
Геометрическое изображение комплексных чисел
Всякое комплексное число можно изобразить на плоскости XOY в виде точки A(x;y), и обратно, всякую точку A(x;y) плоскости XOY можно рассматривать как геометрический образ комплексного числа . При этом ось OY называют мнимой осью, а ось OX – действительной осью. Удобно считать геометрическим изображением комплексного числа вектор 
.
Тригонометрическая форма записи комплексного числа. Модуль и аргумент
Определение 2. Модуль комплексного числа 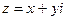обозначается 
и определяется по формуле 
.
Модуль числа z равен длине вектора : 
.
Пример 4. Найти модули комплексных чисел 
и 
.
Решение. 
, 
.
Определение 2. Аргументом комплексного числа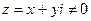 
называется угол между положительным направлением действительной оси и радиус-вектором с началом в точке O(0;0) и концом в точке A(x;y). Угол считается положительным, если отсчёт ведётся против часовой стрелки, и отрицательным, если отсчёт производится по часовой стрелке.
Обозначение: 
, 
.
Заданием модуля и аргумента комплексное число определяется полностью.
Справедливы формулы: 
. (1)
Отсюда комплексное число 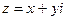может быть представлено в форме:
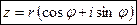. (2)
Формула (2) называется тригонометрической формой записи комплексного числа .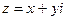
Операции умножения, деления, возведения в степень и извлечения корня над комплексными числами, записанными в тригонометрической форме, осуществляются по формулам:
(3)
(4)
(5)
, где 
. (6)
Формулы (5) и (6) называются формулами Муавра.
Пример 5. Дан модуль комплексного числа r = 2 и его аргумент 
. Найдите действительную и мнимую части комплексного числа.
Решение. По формулам (1) 
, тогда 
.
Пример 6. Дано комплексное число 
. Найдите его модуль и аргумент.
Решение. x= 1, y= 1, 
. По формулам (1) получаем: 
.
Пример 7. Вычислите 
.
Решение. Находим модуль и аргумент числа 
: 
, 
, тогда по формуле (5) получаем 
.
Пример 8. Найдите все значения 
.
Решение. Находим модуль и аргумент числа z = -8: r = 8, 
, тогда по формуле (6) находим 
, где 
. При k = 0 получаем 
, при k = 1 получаем 
, а при k = 2 получаем 
.
Ответ: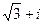 
, -2, 
.