R – генеральная совокупность разбивается на серии. В случайном порядке отбираются целые гнезда (серии) - r -, в которых производится сплошное обследование.
Для определения средней ошибки серийной выборки используем формулы:
а) для доли альтернативного признака
 , (27)
, (27)
где  - межсерийная дисперсия выборочной доли (28)
- межсерийная дисперсия выборочной доли (28)
б) для средней величины количественного признака
 , (29)
, (29)
где  - межсерийная дисперсия выборочной средней. (30)
- межсерийная дисперсия выборочной средней. (30)
Здесь r – число серий в выборке. R - число серий в генеральной совокупности.
По сравнению с типической выборкой серийная дает более высокую ошибку представительности (репрезентативности), т.к. в серийной выборке обычно обследуется небольшое число серий. Для уменьшения ошибки надо увеличивать объем обследуемых серий.
Моментная выборка (моментные выборочные обследования) – для изучения процессов протекающих во времени.
Используется при анализе использования рабочего времени; при анализе времени загрузки оборудования.
Суть этого вида обследования: производится периодическая фиксация (в заранее установленные моменты времени) состояния изучаемой совокупности.
Выборка - сумма периодов, в которые делалась фиксация состояния изучаемых признаков.
Отбор в выборку моментных состояний единиц изучаемой совокупности осуществляется как правило механически. В силу необратимости времени способ отбора должно быть бесповторным. Но поскольку количество моментов времени достаточно большое, то для определения ошибки моментной выборки практически используется формула повторного отбора:  . (31)
. (31)
Главное для моментной выборки – установление ее объема n. На практике для этого применяется формула:  , (32)
, (32)
где w – доля изучаемого признака в выборке;
d – относительная величина предельной ошибки, %
t - кратность ошибки выборки (или коэффициент доверия).
Комбинированная выборка
На практике рассмотренные способы выборки обычно комбинируются в различных сочетаниях и с различной последовательностью.
Так в статистике коммерческой деятельности комбинируют:
- серийный отбор
- случайная выборка.
При этом генеральная совокупность разбивается на серии и отбирается нужное число серий; далее из этих серий проводится случайный отбор единиц в выборочную совокупность.
В этом случае средняя ошибка комбинированной выборки исчисляется по формуле:
а) При повторном отборе:  (33)
(33)
б) При бесповторном отборе:  (34)
(34)
здесь n – число единиц, взятое в выборку из серии.
Отбор бывает: одноступенчатый;
многоступенчатый.
При одноступенчатом отборе каждая отобранная единица сразу подвергается изучению по заданному признаку,
При многоступенчатом отборе из генеральной совокупности отбираются группы, а из них отбираются отдельные единицы.
Комбинированная выборка может быть двухступенчатой.
Средняя ошибка выборки при многоступенчатом отборе:
 , (35)
, (35)
здесь  - средние ошибки выборки на отдельных ступенях отбора;
- средние ошибки выборки на отдельных ступенях отбора;
 - численность выборки на соответствующих ступенях отбора.
- численность выборки на соответствующих ступенях отбора.
Многофазная выборка – когда одни сведения получают от всех единиц, а другие – только по некоторым из них. Сведения, получаемые на первой фазе, могут быть использованы для уточнения расчетов на следующих фазах исследования.
Отличие многофазной выборки от многоступенчатого отбора:
При многофазной выборке на каждой фазе сохраняется одна и та же единица отбора.
При многоступенчатой выборке единица отбора на каждой ступени выборки различна.
28. Понятие о статистических рядах динамики. Виды рядов динамики.
Ряд данных, взятых в определенные периоды времени и представленных в табличной форме называется ряд динамики (временной ряд), т.е. это статистические данные, отображающие развитие изучаемого явления во времени.
В каждом ряду динамики есть два основных элемента:
- показатель времени t,
- соответствующие ему уровни развития изучаемого явления y.
В качестве показателей времени в РД могут быть:
- даты (моменты времени);
- отдельные периоды (сутки, месяцы, кварталы, годы).
Уровни РД отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами. Уровни РД могут относиться к определенным датам (моментам) времени, или к отдельным периодам.
В связи с этим РД делятся на:
Моментные – отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Особенность моментного РД – в его уровни могут входить один и те же единицы изучаемой совокупности. Поэтому при суммировании уровней моментного РД может возникнуть повторный счет.
Интервальные - отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Особенность интервального РД – каждый его уровень складывается их данных за более короткие интервалы (субпериоды) времени. Поэтому можно получать РД более укрупненных периодов (свойство суммирования уровней).
Отображение развития изучаемого явления во времени м.б. представлено РД с нарастающими итогами.
При составлении таких рядов производится последовательное суммирование смежных уровней. Так осуществляется суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (месяц, квартал, год и т.д.)
29. Аналитические показатели ряда динамики и их взаимосвязь.
В основе расчета показателей ряда динамики лежит сравнение его уровней. Показатели динамики могут вычисляться на постоянной и переменной базах сравнения.
При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же базисным уровнем (полученные показатели называются базисными).
При переменной базе сравнения каждый последующий уровень ряда сравнивается с предыдущим (полученные показатели называются цепными).
Исчисляются следующие аналитические показатели ряда динамики:
1. Абсолютный прирост определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Базисный абсолютный прирост ∆yбi
∆yбi= yi- yбi (1)
цепной абсолютный прирост ∆yцi
∆yцi = yi- yц-1 (2)
yi - сравниваемый уровень,
yбi - уровень, принятый за постоянную базу сравнения.
Абсолютный прирост может иметь и отрицательный знак.
Свойство: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики:
∆yбn=Σ∆yцi (3)
2. Темп роста характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах (%).
Базисный темп роста Tрбi определяется делением сравниваемого значения на уровень, принятый за постоянную базу сравнения:
Tрбi = yi / yбi. (4)
Цепной темп роста Tpцi определяется делением сравниваемого уровня на предыдущий:
Tрцi = yi / yц-1 (5)
Свойство: произведение последовательных цепных темпов роста равно базисному темпу роста, а частое от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
3. Темпы прироста характеризуют абсолютный прирост в относительных величинах. Они показывают на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Базисный темп прироста Tпбi определяется как
Tпбi = ∆yбi / yбi. (6)
Цепной темп Tпцi определяется как
Tпцi = ∆yцi / yцi-1 (7)
Взаимосвязь между показателями темпа прироста и темпа роста:
Tпi (%)=Tpi (%)-100 при расчете в процентах (8)
Tпi=Tpi -1 при расчете в коэффициентах. (9)
С использованием приведенных формул одни показатели м.б. определены по другим.
4. Абсолютное значение одного % прироста (снижения) Аi % -
это отношение абсолютного прироста ∆yi за определенный период (обычно за год) к темпу прироста Tпi за этот же период, выраженному в процентах. Этот показатель раскрывает, какая абсолютная величина скрывается за относительной – одним процентом прироста
 (10)
(10)
Количественное значение одного % прироста равно одной сотой части уровня, предшествующего анализируемому. Выражается абсолютное значение одного процента прироста (снижения) в единицах измерения уровней анализируемого РД.
5. Темп наращивания Тнi определяет наращивание во времени исследуемой величины.
Tнi = ∆yцi / yбi., (11)
т.е. определяется делением цепных абсолютных приростов ∆yцi на уровень, принятый за постоянную базу сравнения ∆yцi
 (12)
(12)
Эта формула удобна для практического использования.
30. Средние показатели в рядах динамики.
Для получения обобщающих показателей динамики определяются средние величины.
Средний уровень ряда динамики  характеризует типическую величину абсолютных уровней и определяется делением суммы уровней åyi на их число n:
характеризует типическую величину абсолютных уровней и определяется делением суммы уровней åyi на их число n:
 =
=  . (13)
. (13)
Для моментного ряда динамики с равноотстоящими моментами времени средний уровень исчисляется по формуле:
 (14)
(14)
Для моментного ряда динамики с неравноотстоящими моментами времени средний уровень находится по формуле:
 , (15)
, (15)
здесь уi - уровни ряда, не изменяющиеся в течение промежутка времени ti.
Средний абсолютный прирост 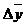 определяется как сумма абсолютных приростов, деленная на их число:
определяется как сумма абсолютных приростов, деленная на их число:
 . (16)
. (16)
Средний абсолютный прирост можно определить по абсолютным уровням как разность конечного уровня ряда и начального (базисного) уровня, деленную на число субпериодов
 (17)
(17)
Средний темп роста  - это обобщающая характеристика индивидуальных темпов роста ряда динамики, определяемая как корень степени n из произведения индивидуальных цепных темпов роста, выраженных в коэффициентах:
- это обобщающая характеристика индивидуальных темпов роста ряда динамики, определяемая как корень степени n из произведения индивидуальных цепных темпов роста, выраженных в коэффициентах:
 , (18)
, (18)
где Трi - индивидуальные (цепные) темпы роста (в коэффициентах), n - их число.
Определим средний темп роста с использованием абсолютных уровней ряда:
 (19)
(19)
Средний темп прироста определяется на основе взаимосвязи между темпами роста и прироста
 при расчете в коэффициентах (20)
при расчете в коэффициентах (20)
31. Сглаживание рядов динамики. Скользящие средние.
Изменение уровней ряда динамики происходит под действием ряда факторов, неоднородных по силе, направлению и времени их действия. Постоянно действующие факторы формируют тренд или основную тенденцию развития. Наиболее распространенными методами статистического изучения тренда являются следующие:
1) Метод укрупнения интервалов. Это один из наиболее простых приемов обнаружения общей тенденции развития явления. Суть этого метода заключается в преобразовании первоначального ряда в ряд динамики с более продолжительным периодом или интервалом времени. При суммировании уровней отклонения, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживается действие основных факторов изменения уровней (общая тенденция).
2) Сглаживание методом скользящей средней.
По исходным данным определяются теоретические уровни, в которых случайные колебания погашаются, а основная тенденция развития выравнивается в виде плавной линии.
Для определения скользящей средней формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получается присоединением одного уровня справа и удалением одного уровня слева. Так мы постепенно сдвигаемся от начального уровня динамического ряда на один уровень. Тогда первый интервал включает уровни от у1 до уm; второй интервал включает уровни от у2 до уm+1 и т.д.
Таким образом, интервал сглаживания как бы скользит по динамическому ряду с шагом, равным единице. По сформированным укрупненным интервалам определяем сумму значений уровней, на основе которых рассчитывается среднее (скользящее среднее). Полученное среднее относится к середине укрупненного интервала. Поэтому технически удобнее укрупненный интервал составлять из нечетного числа уровней ряда. При четном числе уровней ряда в укрупненных интервалах необходима дополнительная процедура центрирования.
Величина интервала сглаживания зависит от средней длины цикла в изучаемом ряду динамики. Это необходимо чтобы исключить циклические колебания. Обычно величина интервала сглаживания равна целому числу, кратному средней длине цикла.
32. Экспоненциальное сглаживание в рядах динамики.
Для выявления долговременных тенденций применяется метод экспоненциального сглаживания. Этот метод позволяет делать краткосрочные прогнозы (в рамках одного интервала), когда наличие долговременных тенденций остается под вопросом.
Метод получил название от последовательности экспоненциально взвешенных скользящих средних. Каждое значение этой последовательности зависит от всех предыдущих наблюдаемых значений.
Уравнение, позволяющее сгладить ряд динамики в пределах произвольного периода времени i содержит три элемента:
Текущее наблюдаемое значение Уi, принадлежащее ряду динамики;
Предыдущее экспоненциально сглаженное значение Еi-1
Присвоенный вес W.
 (21)
(21)
Здесь Еi - экспоненциально сглаженное i-е значение;
Еi-1 - экспоненциально сглаженное i-1-е значение;
Уi - наблюдаемое исходное i - е значение ряда динамики;
W - сглаживающий коэффициент (0<W<1).
Выбор сглаживающего коэффициента достаточно субъективен. Если исследователь хочет просто исключить из ряда динамики нежелательные циклические или случайные колебания, следует выбирать небольшие величины W (близкие к нулю). В этом случае четко проявляются долговременные тенденции.
Если ряд динамики используется для прогнозирования, необходимо выбрать большой вес W (близкий к 1). Тогда повышается точность краткосрочного прогнозирования.
33. Вычисление тренда с помощью метода аналитического выравнивания.
Применение в анализе рядов динамики методов укрупнения интервалов, скользящей средней, экспоненциального сглаживания позволяет выявить тренд для его описания, но получить обобщенную статистическую оценку тренда посредством этих методов не возможно. Решение этой более высокого порядка задачи достигается методом аналитического выравнивания.
Метод аналитического выравнивания. Он позволяет получить обобщенную статистическую оценку тренда. Тренд yt рассчитывается как функция времени.
 . (22)
. (22)
Определение теоретических (расчетных) уровней  производится на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития ряда динамики.
производится на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития ряда динамики.
Подбор математической функции осуществляется методом наименьших квадратов
 . (23)
. (23)
Таким образом, сумма отклонений между теоретическими  и эмпирическими (полученными на практике) уровнями
и эмпирическими (полученными на практике) уровнями  должна быть минимальна.
должна быть минимальна.
Формула (8.23) – это критерий соответствия расчетных и фактических уровней РД.
Главное здесь – подбор математической функции.
Различают следующие эталонные типы развития явлений во времени:
а) равномерное развитие – если абсолютные приросты в РД постоянны:
∆уц ≈ const.
Основная тенденция развития в РД со стабильными абсолютными приростами отображается уравнением прямолинейной функции (линейный тренд):
 (24)
(24)
Здесь а0, а1 - параметры уравнения; t - обозначение времени.
Параметр а1 является коэффициентом регрессии, определяющим направление развития. Если а1 > 0, то уровни РД равномерно возрастают, при а1 < 0 происходит равномерное снижение уровней РД.
б) равноускоренное (равнозамедленное) развитие – уровни таких РД изменяются с постоянными темпами прироста:
Tпцi ≈ const
Основная тенденция развития в РД со стабильными темпами прироста отображается функцией параболы второго порядка (квадратичный тренд):
 (25)
(25)
Здесь значения параметров а0, а1 идентичны параметрам линейного тренда,
а2 - параметр, характеризующий изменение интенсивности развития в единицу времени (ускорение развития или процесс замедления роста).
в) развитие с переменным ускорением (замедлением) – парабола третьего порядка:
 (26)
(26)
а3 - параметр, отображающий изменение ускорения.
г) развитие по экспоненте – для стабильных темпов роста. Математически это показательная функция:
 (27)
(27)
д) развитие с замедлением роста в конце периода (показание абсолютного прироста сокращается в конечных уровнях ряда динамики). Математически это полулогарифмическая функция:
 (28)
(28)
При изучении неудовлетворенного и реализованного спроса применяют:
е) степенную функцию:
 (29)
(29)
ж) функцию гиперболы:
 (30)
(30)
На практике выбор эталонной математической функции достаточно сложная и трудоемкая операция (даже при использовании соответствующего программного обеспечения). Особенно это имеет место для криволинейных функций, теория которых разработана недостаточно.
Для вычисления параметров функции линейного тренда на основе метода наименьших квадратов составляется система нормальных уравнений:
 (31)
(31)
Для решения системы применяется способ определителей, позволяющий получать более точные результаты за счет сведения к минимуму ошибки из-за округлений в расчетах параметров:
 (32)
(32)
Здесь значения времени – это целые числа (коды).
Для упрощения расчетов используется специальный подбор показателей времени так, чтобы их сумма равнялась нулю (способ расчета времени от условного начала):

Например, если число уровней в РД нечетное и равно 7, условные значения показателей времени равны:
-7 -5 -3 -1 0 1 3 5 7
Тогда расчет коэффициентов линейного тренда значительно упрощается и м.б. выполнен по формулам:
 (33)
(33)
После определения параметров линейного тренда подставляем их в искомое линейное уравнение и находим теоретические (выровненные) значения  .
.
Одним из наиболее часто применяемых показателей адекватности математической функции (математической модели) является стандартизованная ошибка аппроксимации:

 (34)
(34)
Она должна быть минимальна у выбранной теоретической модели тренда.
Расхождения между теоретическими и практическими значениями доходов характеризуются среднеквадратической ошибкой аппроксимации.
Аналогичным образом строится модель квадратичного, экспоненциального и других видов тренда.
По виду функции (см. рис.) наметим типы функций для анализа:
1) - прямолинейная,
2) - показательная функция,
3) - парабола второго порядка.
1) для прямолинейной функции:

2) для показательной функции

3) для параболы 2-го порядка:

34. Прогнозирование в рядах динамики.
Экономические условия изменяются с течением времени. Поэтому менеджеры должны прогнозировать влияние, которое эти изменения окажут на их компанию. Одним из методов, позволяющих обеспечить точное планирование, является прогнозирование (forecasting). Несмотря на большое количество разработанных методов прогнозирования, все они преследуют одну и ту же цель – предсказать события, которые произойдут в будущем, чтобы учесть их при разработке планов и стратегии развития компании. Если статистику доступны данные об объекте исследования, применяются количественные методы прогнозирования (quantitative forecasting methods). Эти методы позволяют предсказать состояние объекта в будущем на основе данных о его прошлом и настоящем. Методы количественного прогнозирования разделяются на две категории:
ü анализ рядов динамики (временных рядов);
ü методы анализа причинно-следственных зависимостей.
Метод анализа рядов динамики позволяет предсказать значение числовой переменной на основе ее прошлых и настоящих значений.
Методы анализа причинно-следственных зависимостей позволяют определить, какие факторы влияют на значения прогнозируемой переменной. К ним относятся методы множественного регрессионного анализа с запаздывающими переменными, эконометрическое моделирование, анализ лидирующих индикаторов, методы анализа диффузионных индексов и других экономических показателей.
При прогнозировании важно:
ü установить продолжительность базисного ряда динамики (необходимо использовать те субпериоды базисного РД, которые составляют определенный этап в развитии изучаемого явления в конкретных условиях);
ü установить сроки прогнозирования (чем короче сроки прогнозирования, тем надежнее его результаты).
На практике результат прогнозирования м.б. выполнен не точечными (дискретными), а интервальными оценками. Для определения границ интервалов используется формула:
 (35)
(35)
где  - коэффициент доверия по распределению Стьюдента при уровне значимости α;
- коэффициент доверия по распределению Стьюдента при уровне значимости α;
 (36)
(36)
- остаточное среднеквадратическое отклонение тренда, скорректированное по числу степеней свободы n-m; n - число уровней базисного ряда динамики; m - число параметров адекватной модели тренда.
35. Компоненты классической мультипликативной модели рядов динамики.
Основное предположение, лежащее в основе анализа рядов динамики, состоит в следующем: факторы, влияющие на исследуемый объект в настоящем и прошлом, будут влиять на него и в будущем. Таким образом, основные цели анализа РД заключаются в идентификации и выделении факторов, имеющих значение для прогнозирования.
Для достижения этой цели, разработаны математические модели, предназначенные для исследования колебаний компонентов, входящих в модель ряда динамики. Наиболее распространенной является классическая мультипликативная модель для ежегодных, ежеквартальных и ежемесячных данных.
Тренд - не единственный компонент ряда динамики. Кроме него данные имеют циклический и нерегулярный компоненты. Циклический компонент описывает колебание данных вверх и вниз, часто коррелируя с циклами деловой активности. Его длина может изменяться в интервале от 2 до 10 лет. Интенсивность или амплитуда циклического компонента непостоянна. В некоторые годы данные м.б. выше значения, предсказанного трендом (т.е. находиться в окрестности пика цикла) а в другие годы – ниже (т.е. быть на дне цикла). Любые наблюдаемые данные, не лежащие на кривой тренда и не подчиняющиеся циклической зависимости, называются иррегулярными или случайными компонентами. Если данные записываются ежемесячно или ежеквартально, возникает дополнительный компонент, называемый сезонным.
Все компоненты рядов динамики, характерные для экономических приложений, приведены в табл.
Таблица. Компоненты колебаний уровней в рядах динамики
| Компо-ненты | Вид | Определение | Причины | Продолжительность |
| Тренд | Системати-ческий | Описывает долговременное возрастание или убывание данных | Изменения технологии, населения, благосостояния, рыночных цен | Несколько лет |
| Сезон-ный | Системати-ческий | Описывает четко выра-женные периодические колебания, прояв-ляющиеся ежегодно | Погодные условия, социальное поведение, обычаи | В течение года (месяца или квартала |
| Цикли-ческий | Системати-ческий | Повторяющиеся коле-бания, имеющие 4 фазы: пик (процветание), спад (рецессия), дно (депрес-сия) и подъем (восста-новление или рост) | Взаимодействие многочисленных факторов, влияющих на экономическую активность | Как правило с переменной интенсивностью на протяжении 2-10 лет |
| Случай-ный | Несистематический | Случайные колебания РД, возникающие после учета систематических эффектов | Случайные колебания данных или непредвиденные события (ураганы, наводнения, забастовки) | Кратковременные и однократные |
Классическая мультипликативная модель РД утверждает, что любое наблюдаемое явление является произведением перечисленных компонентов. Если данные являются ежегодными, наблюдаемое значение Уi, соответствующее i -му году, выражается следующим уравнением.
Классическая мультипликативная модель РД для ежегодных данных:
Уi =Тi *Сi *Ii, (37)
где Тi - значение тренда; Сi - значение циклического компонента; Ii - значение случайного компонента в i -м году.
Если данные измеряются ежемесячно или ежеквартально, наблюдение Уi, соответствующее i -му периоду, выражается следующим уравнением.
Классическая мультипликативная модель РД для данных с учетом сезонного компонента:
Уi =Тi *Si *Сi *Ii, (38)
где Тi - значение тренда; Si - значение сезонного компонента в i -м периоде; Сi - значение циклического компонента; Ii - значение случайного компонента в i -м периоде.
На первом этапе анализа РД строится график данных и выявляется их зависимость от времени. Сначала определяется, существует ли долговременное возрастание или убывание данных (т.е. тренд). Если тренд отсутствует, то для сглаживания данных можно применить метод укрупнения интервалов, скользящих средних или экспоненциального сглаживания. Если реальный тренд существует, открывается возможность применять методы прогнозирования для различных видов математических функций.
36. Изучение сезонных изменений.
Сезонные изменения (колебания) – это устойчивые внутригодовые колебания уровней развития явлений. Полностью устранить их не возможно. Их надо учитывать, с ними надо считаться.
В ходе статистического анализа сезонных колебаний решаются важнейшие для экономической практики задачи. Это, во-первых, оптимизация распределения по месяцам в течение года производственных ресурсов и, во-вторых, реализация комплекса производственных мероприятий, позволяющих сократить сезонные колебания, обеспечив тем самым более или менее равномерную занятость производственного персонала, а также финансовую и экономическую стабильность.
При изучении сезонных колебаний выполняется:
ü Выявление специфики развития изучаемого явления во внутригодовой динамике;
ü Измерение сезонных колебаний изучаемого явления с построением модели сезонной волны.
Для изучения сезонных колебаний ряды динамики должны быть приведены к сопоставимому виду:
v сопоставимость или одинаковость показаний времени, его интервалов, однородность состава изучаемых совокупностей во времени.
v однородность состава изучаемых совокупностей во времени;
v одни единицы измерения, цены;
v единая методика обобщения исходной информации и т.д.
Для измерения сезонных колебаний исчисляют индексы сезонности:
 , (39)
, (39)
которые представляют собой отношение эмпирических уровней РД уi к теоретическим (расчетным) уровням уti.
Расчетные уровни выступают в качестве базы сравнения. Таким образом, элиминируется влияние основной тенденции развития при расчете индексов сезонности.
Совокупность индексов сезонности образует сезонную волну.
Чтобы выявить устойчивую сезонную волну, в которой не учитывались бы исключительные условия одного года, средние индексы сезонности исчисляют, как правило, за три года и более:
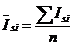 (40)
(40)
Существуют различные методы нахождения индексов сезонности, которые используют в зависимости прежде всего от характера основной тенденции ряда динамики.
1. Для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития вначале производят выравнивание ряда методом 12-членной скользящей средней или методом аналитического выравнивания, затем рассчитывают индексы сезонности:
 (41)
(41)
Здесь уti - средняя ось кривой, т.к. ее расчет основан на методе наименьших квадратов. Для определения теоретических уровней тренда важно правильно подобрать математическую функцию, по которой будет производиться аналитическое выравнивание в анализируемом РД. Измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней.
2. Для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд отсутствует или он незначителен, индексы сезонности находят по формуле:
 (42)
(42)
Здесь база для сравнения  - общий для анализируемого ряда средний уровень. По указанной формуле индексы сезонности рассчитывают способом постоянной средней.
- общий для анализируемого ряда средний уровень. По указанной формуле индексы сезонности рассчитывают способом постоянной средней.
37. Понятие статистического индекса. Индивидуальные и общие индексы.
Само слово (index) означает показатель. Представим индексы прежде всего как показатели изменений.
Особенности индексов:
ü Позволяют измерить изменение сложных явлений;
ü Выявляют роль отдельных факторов;
ü Сравнения могут осуществляться с прошлым периодом, с другой территорией или с нормативами.
Индекс - это показатель сравнения двух состояний одного и того же явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов).
Каждый индекс включает два вида данных:
- оцениваемые данные или отчетные или текущие. Они обозначаются значком "1".
- данные, которые используются в качестве базы сравнения - базисные, они обозначаются значком "0".
Индекс, который строится как сравнение обобщенных величин, называется сводным или общим (сложным). Он обозначается I. Если сравниваются необобщенные величины, то индекс называется индивидуальным (простым) и обозначается i.
Основным элементом индексного отношения является индексируемая величина.
Индивидуальные индексы физического объёма реализации товаров определяются по формуле (q – quantity - количество):
iq = q1:q0, (1)
где q1, q0 - количество продажи отдельного товара в текущем и базисном периодах в натуральных измерителях.
Индивидуальный индекс цен (p – price – цена) определяется как:
ip = p1:p0, (2)
где p1, p0 - цены за единицу товара в текущем и базисном периодах.
Результаты расчета индексных отношений выражаются в коэффициентах или в процентах.
Общие индексы могут исчисляться как по агрегатной, так и по средней форме (среднего арифметического или среднего гармонического индекса).
38. Агрегатные индексы.
Происходят от латинского слова «aggrega» - присоединяю. В числителе и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых статистических совокупностей:
Индексируемая величина * Соизмеритель
изменяется в числителе для перехода к однородным
и знаменателе показателям – неизменен
Общий индекс цен, если соизмеритель q1 - данные о количестве реализации товаров в текущем периоде, это индекс Пааше:
 . (3)
. (3)
Общий индекс цен, если соизмеритель q0, называется индексом Ласпейреса:
 . (4)
. (4)
Формулы (3) и (4) определяют агрегатные индексы, т.е. индексы в числителе и знаменателе которых находятся произведения индексируемой величины на соизмеритель.
Формулы (3) и (4) могут быть распространенны на индексы других качественных показателей:
- себестоимости Iz,
- производительности труда It и т.д.
Агрегатные индексы можно определить для физического объёма товарной массы q:
- в ценах базисного периода p0
 , (5)
, (5)
- в ценах текущего периода p1
 . (6)
. (6)
При индексном методе анализа коммерческой деятельности надо учитывать, что факторы, влияющие на объем товарооборота – количество реализации и их цены действуют одновременно. В анализе важно определить общий результат их совокупного взаимодействия.
Из формул (3)... (5) строится общий индекс товарооборота
 (7)
(7)
В этом индексе производится сравнение двух качественно однородных величин (стоимостей)
39. Средние индексы.
а) При синтезировании общего индекса цен вместо фактического количества товаров (в отчетный или базисный периоды) в качестве соизмерителя могут применяться средние величины реализации товаров за два или большее количество периодов. Примером такого среднего индекса является индекс Лоу
 (8)
(8)
Здесь  - среднее количество товаров, реализованных за анализируемый период. Если есть только два периода – базисный и текущий, то средняя величина определяется по формуле средней невзвешенной.
- среднее количество товаров, реализованных за анализируемый период. Если есть только два периода – базисный и текущий, то средняя величина определяется по формуле средней невзвешенной.
б) Для определения сводных обо