Предисловие
В течение нескольких десятилетий кафедра высшей математики каждый год организует и проводит внутривузовскую олимпиаду по математике для студентов 1 и 2-го курсов технических и экономических специальностей.
В последние годы кафедра проводит командные олимпиады (команда до 5-ти человек), при этом студенты организуют свои команды сами, как правило, по специальностям. Ежегодно в олимпиаде участвуют 250-350 студентов младших курсов.
В изложенных в работе олимпиадных заданиях (2005-2009 гг) задачи имеют различную степень трудности, но их содержания и решения в любом случае не выходят за рамки изучаемого в ОмГТУ общего курса математики. Мы стремились изложить решение задач так, чтобы студенты могли разобраться в них самостоятельно.
Методические указания могут быть использованы как преподавателями, готовящими студентов к различным математическим олимпиадам, так и студентами при подготовке к участию в них.
Задания
ОЛИМПИАДА -2005 год
Й курс
Найти все тройки действительных чисел  для которых для которых  , где , где 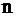 - некоторое натуральное число, - некоторое натуральное число, 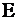 - единичная матрица. - единичная матрица.
| |
Найти все действительные корни уравнения  . .
| |
Пусть  . Показать, что существует число . Показать, что существует число  из из  такое, что такое, что  . .
| |
| Две вершины треугольника зафиксированы, а третья движется по плоскости так, что один из углов при основании треугольника остается вдвое больше другого. Какую линию описывает третья вершина? | |
Пусть  - четыре точки пространства, - четыре точки пространства,  , ,  , ,  и и  . Показать, что точки . Показать, что точки 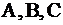 лежат на одной прямой. лежат на одной прямой.
| |
Вычислить  . .
| |
| В произвольном выпуклом шестиугольнике соединены середины противоположных сторон. Всегда ли из полученных отрезков можно сложить треугольник? | |
Вычислить  . .
| |
Найти значение производной 2005-го порядка функции  в точке в точке  . .
| |
Функция  дважды дифференцируема и удовлетворяет равенству дважды дифференцируема и удовлетворяет равенству  , где , где  на всей числовой оси. Доказать, что на всей числовой оси. Доказать, что  и и  - ограничены на всей числовой оси. - ограничены на всей числовой оси.
|
Й курс
Найти все тройки действительных чисел  для которых для которых  , где , где 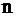 - некоторое натуральное число, - некоторое натуральное число,  - единичная матрица. - единичная матрица.
| |
Вычислить  , где , где  ограничена линиями: ограничена линиями:  , ,  , ,  . .
| |
Пусть  . Показать, что существует число . Показать, что существует число  из из  такое, что такое, что  . .
| |
| Две вершины треугольника зафиксированы, а третья движется по плоскости так, что один из углов при основании треугольника остается вдвое больше другого. Какую линию описывает третья вершина? | |
Функция  непрерывна на непрерывна на  . Показать, что . Показать, что  . .
| |
Показать, что  . .
| |
Найти значение производной 2005-го порядка функции  в точке в точке  . .
| |
Функция  дважды дифференцируема и удовлетворяет равенству дважды дифференцируема и удовлетворяет равенству  , где , где  на всей числовой оси. Доказать, что на всей числовой оси. Доказать, что  и и  - ограничены на всей числовой оси. - ограничены на всей числовой оси.
| |
Доказать равенство  . .
| |
Сколько положительных корней имеет многочлен  , если , если 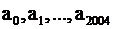 - положительные числа? - положительные числа?
|
ОЛИМПИАДА -2006 год
Й курс
Вычислить  . .
| |
Можно ли через прямые   провести плоскость? провести плоскость?
| |
Вычислить  . .
| |
Построить линию  . .
| |
Решить уравнение  , , 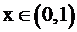 . .
| |
| Координаты всех вершин многоугольника на плоскости – рациональные числа. Доказать, что площадь многоугольника – рациональное число. | |
Найти все ограниченные в окрестности нуля функции  , удовлетворяющие тождеству , удовлетворяющие тождеству 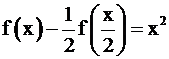 . .
| |
Через точку (0,0,1) проведены все прямые с направляющими векторами  , где , где  – любое действительное число. По каким линиям пересекается полученная поверхность с плоскостями, перпендикулярными осям координат? – любое действительное число. По каким линиям пересекается полученная поверхность с плоскостями, перпендикулярными осям координат?
| |
Все элементы квадратной матрицы  порядка порядка 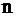 – числа 0; 1 или -1, причем каждая строка и столбец содержат ровно один ненулевой элемент. Доказать, что – числа 0; 1 или -1, причем каждая строка и столбец содержат ровно один ненулевой элемент. Доказать, что  , где , где 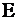 – единичная матрица, а – единичная матрица, а  – некоторое натуральное число. – некоторое натуральное число.
| |
| Вертолет должен пролететь 25 км на север, затем 200 км на восток при постоянном по направлению и величине векторе скорости, причем скорость ветра равна собственной скорости вертолета. При каком направлении ветра на полет уйдет минимальное время? |
Й курс
Вычислить  . .
| |
Можно ли через прямые   провести плоскость? провести плоскость?
| |
При каких значениях действительного числа  сходится ряд сходится ряд  ? ?
| |
Решить уравнение  . .
| |
| Координаты всех вершин многоугольника на плоскости – рациональные числа. Доказать, что площадь многоугольника – рациональное число. | |
Найти площадь эллипса, образованного пересечением цилиндра  и плоскости и плоскости  . .
| |
Найти все ограниченные в окрестности нуля функции  , удовлетворяющие тождеству , удовлетворяющие тождеству 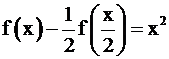 . .
| |
Вычислить  . .
| |
Все элементы квадратной матрицы  порядка порядка 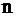 – числа 0; 1 или -1, причем, каждая строка и столбец содержит ровно один ненулевой элемент. Доказать, что – числа 0; 1 или -1, причем, каждая строка и столбец содержит ровно один ненулевой элемент. Доказать, что  , где , где 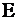 – единичная матрица, а – единичная матрица, а  – некоторое натуральное число. – некоторое натуральное число.
| |
Функция  – дифференцируема и удовлетворяет тождеству – дифференцируема и удовлетворяет тождеству
 .
Доказать, что при .
Доказать, что при   . .
|
ОЛИМПИАДА -2007 год
Й курс
Построить график функции  . .
| |
Вычислить  . .
| |
Составить уравнения всех окружностей, проходящих через точки  и и 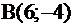 . .
| |
Пусть  - вершины правильного n-угольника, вписанного в окружность радиуса 1. Вычислить - вершины правильного n-угольника, вписанного в окружность радиуса 1. Вычислить  . .
| |
Функция  удовлетворяет условиям удовлетворяет условиям  , ,  . Доказать, что . Доказать, что  нельзя представить в виде отношения двух многочленов. нельзя представить в виде отношения двух многочленов.
| |
Изобразить множество точек  плоскости, для которых выполнено неравенство плоскости, для которых выполнено неравенство  . .
| |
Вычислить 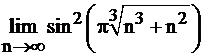 . .
| |
Действительная функция  определена на всей числовой оси и удовлетворяет тождеству определена на всей числовой оси и удовлетворяет тождеству  , где , где  – заданная постоянная, – заданная постоянная,  . Доказать, что . Доказать, что  – периодическая и привести пример непостоянной функции с указанными свойствами. – периодическая и привести пример непостоянной функции с указанными свойствами.
| |
| На маленьком острове стоит прожектор, освещающий отрезок моря длиной 1 км. Прожектор вращается равномерно вокруг вертикальной оси, делая один оборот в минуту. Сможет ли подплыть к острову незаметно катер, имеющий скорость 0,9 км/мин? | |
В невырожденной квадратной матрице  порядка порядка 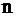 сумма элементов любой строки равна 1. Найти сумму всех элементов обратной матрицы сумма элементов любой строки равна 1. Найти сумму всех элементов обратной матрицы  . .
|
Й курс
| Найти все функции, у которых вторая производная совпадает с пятой. | |
Доказать, что касательные плоскости к поверхности  отсекают на осях координат отрезки, сумма длин которых не зависит от выбора точки касания. отсекают на осях координат отрезки, сумма длин которых не зависит от выбора точки касания.
| |
Составить уравнения всех окружностей, проходящих через точки  и и 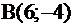 . .
| |
Привести пример такого сходящегося знакоположительного ряда 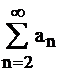 , что ряд , что ряд  расходится. расходится.
| |
Построить интегральную кривую (график решения) задачи Коши  . .
| |
Изобразить множество точек  плоскости, для которых выполнено неравенство плоскости, для которых выполнено неравенство  . .
| |
Вычислить  . .
| |
Действительная функция  определена на всей числовой оси и удовлетворяет тождеству определена на всей числовой оси и удовлетворяет тождеству  , где , где  – заданная постоянная, – заданная постоянная,  . Доказать, что . Доказать, что  – периодическая и привести пример непостоянной функции с указанными свойствами. – периодическая и привести пример непостоянной функции с указанными свойствами.
| |
| На маленьком острове стоит прожектор, освещающий отрезок моря длиной 1 км. Прожектор вращается равномерно вокруг вертикальной оси, делая один оборот в минуту. Сможет ли подплыть к острову незаметно катер, имеющий скорость 0,9 км/мин? | |
В невырожденной квадратной матрице  порядка порядка 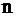 сумма элементов любой строки равна 1. Найти сумму всех элементов обратной матрицы сумма элементов любой строки равна 1. Найти сумму всех элементов обратной матрицы  . .
|
ОЛИМПИАДА -2008 год
Й курс
У студента стал «глючить» его любимый калькулятор. Он может только складывать и вычитать данные числа и вычислять обратное к данному числу  , т.е. , т.е.  . Как ему, используя только этот калькулятор, для данного числа . Как ему, используя только этот калькулятор, для данного числа  вычислить вычислить  ? ?
| |
Существует ли  , при котором определитель порядка 2008, в котором , при котором определитель порядка 2008, в котором  , равен нулю? , равен нулю?
| |
Построить график функции  . .
| |
Доказать, что уравнение  имеет хотя бы одно решение в интервале имеет хотя бы одно решение в интервале  . .
| |
Вычислить  . .
| |
В треугольной пирамиде  - площадь - площадь  -ой грани, -ой грани,  - единичная внешняя нормаль - единичная внешняя нормаль  -ой грани -ой грани  . Доказать, что . Доказать, что  . .
| |
Решить уравнение  . .
| |
Доказать, что на плоскости существует единственный равносторонний треугольник, координаты всех вершин которого удовлетворяют уравнению  и найти его площадь. и найти его площадь.
|
Й курс
У студента стал «глючить» его любимый калькулятор. Он может только складывать и вычитать данные числа и вычислять обратное к данному числу  , т.е. , т.е.  . Как ему, используя только этот калькулятор, для данного числа . Как ему, используя только этот калькулятор, для данного числа  вычислить вычислить  ? ?
| |
Существует ли  , при котором определитель порядка 2008, в котором , при котором определитель порядка 2008, в котором  , равен нулю? , равен нулю?
| |
Могут ли функции  быть решением на быть решением на  дифференциального уравнения дифференциального уравнения 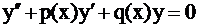 с непрерывными коэффициентами с непрерывными коэффициентами  ? ?
| |
Доказать, что уравнение  имеет хотя бы одно решение в интервале имеет хотя бы одно решение в интервале  . .
| |
Пусть  на на 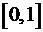 и и  , ,  . Найти . Найти  . .
| |
Найти сумму ряда  . .
| |
Решить уравнение  . .
| |
Вычислить 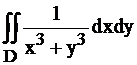 , где , где  . .
|
ОЛИМПИАДА -2009 год
Й курс
| Найти уравнения всех общих касательных к окружностям радиусов 3 и 4 с центрами в точках (0,5) и (5,0) соответственно. | |
Найти площадь четырехугольника, стороны которого лежат на прямых  , ,  , ,  , ,  . .
| |
Сколько действительных решений имеет уравнение  ? ?
| |
Найти максимальное значение определителя  , где , где  - квадратная матрица, в каждой строке и столбце которой одна единица, а остальные элементы – нули. - квадратная матрица, в каждой строке и столбце которой одна единица, а остальные элементы – нули.
| |
Построить график функции 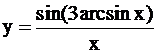 . .
| |
Вычислить  . .
| |
При каких 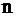 система система  имеет решение? имеет решение?
| |
Найти наибольшее значение функции  на на  ( (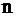 - любое натуральное число). - любое натуральное число).
| |
Найти все  такие, что для любых такие, что для любых  выполняется выполняется  . .
| |
При каком  абсцисса точки перегиба функции абсцисса точки перегиба функции  имеет наименьшее натуральное значение? имеет наименьшее натуральное значение?
|
Й курс
| Записать уравнение круговой цилиндрической поверхности радиуса 1, ось которой проходит через точки (0, 0, 0) и (1, 1, 1) | |
Решить задачу Коши  . .
| |
Вычислить 
| |
Найти все решения матричного уравнения  , где , где  , , 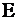 - единичная матрица. - единичная матрица.
| |
Исследовать сходимость ряда 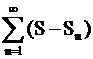 , где , где  - сумма ряда - сумма ряда  , а , а  - его частичные суммы. - его частичные суммы.
| |
Вычислить предел 
| |
При каких 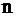 система система  имеет решение? имеет решение?
| |
Найти наибольшее значение функции  на на  ( (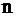 - любое натуральное число). - любое натуральное число).
| |
Найти все  такие, что для любых такие, что для любых  выполняется выполняется  . .
| |
При каком  абсцисса точки перегиба функции абсцисса точки перегиба функции  имеет наименьшее натуральное значение? имеет наименьшее натуральное значение?
|
Решения
ОЛИМПИАДА -2005 год
Й курс
1. Индукцией по степени 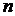 легко проверяется, что
легко проверяется, что
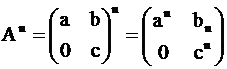 ,
,
где
 ,
,  . (*)
. (*)
По условию  при некотором
при некотором  , первое из этих равенств возможно только при
, первое из этих равенств возможно только при 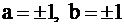 .
.
Если 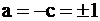 , то из (*) следует
, то из (*) следует  и
и  , т.е. тройки
, т.е. тройки  и
и  удовлетворяют условию при любых
удовлетворяют условию при любых  .
.
Если  , (*) запишется в виде
, (*) запишется в виде  ,
,  и
и  возможно только при
возможно только при  , а при
, а при 
 .
.
Если  , то
, то  ,
,  только при
только при  , а при
, а при 
 .
.
Ответ:  ,
,  ;
;  ,
,  .
.
2.  при
при 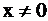 . Следовательно левая часть уравнения строго возрастает.
. Следовательно левая часть уравнения строго возрастает.
 - единственный корень.
- единственный корень.
3.  т.к. третья строка определителя становится пропорциональной первой;
т.к. третья строка определителя становится пропорциональной первой;
 т.к. вторая строка определителя становится пропорциональной первой.
т.к. вторая строка определителя становится пропорциональной первой.
Так как  , то утверждение следует из теоремы Ролля.
, то утверждение следует из теоремы Ролля.
4. Введем систему координат и необходимые обозначения

| По теореме синусов
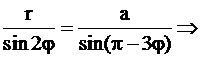

 . .
|
Т.к.  , то
, то  . Далее с учетом
. Далее с учетом 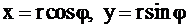 получаем
получаем

 - уравнение гиперболы.
- уравнение гиперболы.
5. Зададим векторную функцию четырех точек пространства равенством




 лежат на одной прямой.
лежат на одной прямой.
6. 

7.

| 

|
Ответ: да, всегда.
8. Пусть  - искомый предел. Тогда
- искомый предел. Тогда

9. Функция преобразуется по тригонометрическим формулам в сумму:

 10. Умножим дифференциальное уравнение на
10. Умножим дифференциальное уравнение на  :
:

или
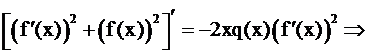 функция
функция  не убывает при
не убывает при  и не возрастает при
и не возрастает при 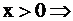
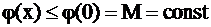 т.е.
т.е. 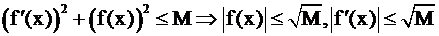 ч.т.д.
ч.т.д.
Й курс
1. см. 2005, 1 курс, №1.
2. Область  имеет вид
имеет вид

 .
.
3. см. 2005, 1 курс, №3.
4. см. 2005, 1 курс, №4.
5.
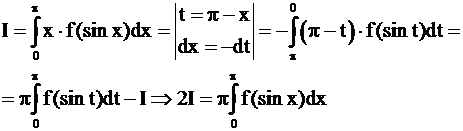
ч.т.д.
6. Исследуем  и используем неравенство
и используем неравенство  .
.
 , т.е.
, т.е. 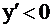 при
при  , и
, и  при
при  .
.
Тогда  ч.т.д.
ч.т.д.
7. см. 2005, 1 курс, №9.
8. см. 2005, 1 курс, №10.
9.  , где
, где  .
.
Имеем 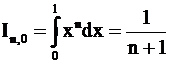 , а при
, а при 

 по индукции
по индукции 
 ч.т.д.
ч.т.д.
10. Очевидно, что

 один раз меняет знак с – на + на
один раз меняет знак с – на + на 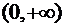 ,
, 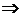
 один раз меняет знак с – на + на
один раз меняет знак с – на + на 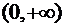 ,…,
,…, 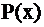 один раз меняет знак с – на + на
один раз меняет знак с – на + на 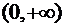 , т.е.
, т.е.  имеет ровно 1 положительный корень.
имеет ровно 1 положительный корень.
ОЛИМПИАДА -2006 год
Й курс
1.  .
.
2. Через прямые  и
и 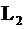 можно провести плоскость в двух случаях: 1)
можно провести плоскость в двух случаях: 1)  2)
2)  .
.
В данной задаче  и
и 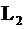 не параллельны, т.к. их направляющие векторы
не параллельны, т.к. их направляющие векторы  ,
,  . Ищем точку пересечения
. Ищем точку пересечения  и
и 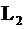 (
(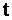 и
и 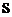 - обозначения параметров в уравнениях
- обозначения параметров в уравнениях  и
и 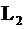 ):
):

Ответ: можно, т.к.  .
.
3. а) 
б)  (правило Лопиталя)
(правило Лопиталя)  .
.
Ответ:  .
.
4. 
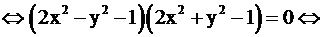
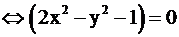 или
или 
 (гипербола) или
(гипербола) или  (эллипс)
(эллипс)
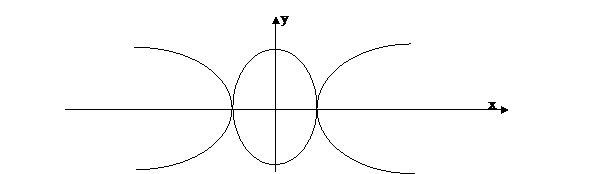
5.
 ,
, 

(сумма бесконечно убывающей геометрической прогрессии). Матричное равенство из условия эквивалентно системе уравнений:
 .
.
6. Для треугольника с вершинами  ,
,  ,
,  :
:

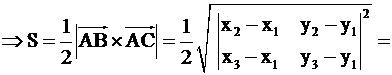
 рациональное.
рациональное.
Площадь многоугольника равна сумме площадей треугольников, т.е. сумме рациональных чисел.
7. По условию  для любого
для любого  .
.
В частности,
 . Отсюда последовательно получаем
. Отсюда последовательно получаем
 ;
;
 ;
;
………………………………………………………………………
 (*)
(*)
При  имеем
имеем  , и в силу ограниченности
, и в силу ограниченности  в окрестности
в окрестности 
 .
.
Теперь из (*) при  и формулы суммы геометрической прогрессии получаем
и формулы суммы геометрической прогрессии получаем
 .
.
8. Параметрические уравнения прямых имеют вид:
 - уравнение поверхности из условия задачи.
- уравнение поверхности из условия задачи.
1) 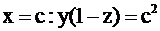 - пара перпендикулярных прямых (
- пара перпендикулярных прямых ( ), гипербола (
), гипербола ( ).
).
2)  - прямая (
- прямая ( ), парабола (
), парабола ( ).
).
3)  - прямая (
- прямая ( ), парабола (
), парабола ( ).
).
9. Пусть  - множество всех матриц указанного вида. Тогда
- множество всех матриц указанного вида. Тогда
1)  , т.к. для любой строки
, т.к. для любой строки  (любого столбца
(любого столбца  ) существует ровно один столбец
) существует ровно один столбец  (строка
(строка  ) такие, что произведение строки
) такие, что произведение строки  на столбец
на столбец  не равно 0 (и равно
не равно 0 (и равно  ).
).
2) Число различных матриц в  конечно (
конечно ( ) т.к. число различных первых строк равно
) т.к. число различных первых строк равно  , для каждого выбора первой строки
, для каждого выбора первой строки 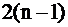 выборов второй и т.д.
выборов второй и т.д.
Из 1) и 2) следует, что при  в последовательности
в последовательности  есть по крайней мере две совпадающие
есть по крайней мере две совпадающие  . Т.к.
. Т.к.  - невырожденная матрица (
- невырожденная матрица ( ), то
), то  . Ч.т.д.
. Ч.т.д.
10. Введем систему координат, в которой OX направлена на восток, OY – на север. Пусть  - собственная скорость вертолета,
- собственная скорость вертолета,  - угол вектора скорости ветра
- угол вектора скорости ветра  с направлением на север. Очевидно, что для минимального времени полета
с направлением на север. Очевидно, что для минимального времени полета  и
и  (т.к.
(т.к.  ).
).
Пусть  - вектор собственной скорости вертолета при полете на север. Тогда
- вектор собственной скорости вертолета при полете на север. Тогда  , и время полета на север
, и время полета на север  .
.
Аналогично, 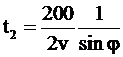 - время полета на восток. Общие затраты времени
- время полета на восток. Общие затраты времени  и
и 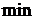 времени достигается при
времени достигается при  .
.
Й курс
1. см. 2006, 1 курс, №1.
2. см. 2006, 1 курс, №2.
3. 1)  - расходится по необходимому признаку.
- расходится по необходимому признаку.
2)  -расходится по признаку сравнения т.к.
-расходится по признаку сравнения т.к. 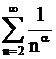 - расходится при
- расходится при  .
.
3) При  положим
положим 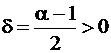 и сравним наш ряд
и сравним наш ряд  со сходящимся рядом
со сходящимся рядом  (обобщенный гармонический ряд):
(обобщенный гармонический ряд):
 (правило Лопиталя)
(правило Лопиталя) 
 для любого
для любого 
 начиная с некоторого номера
начиная с некоторого номера 
 - сходится.
- сходится.
Замечание. При  функция
функция  положительна (при
положительна (при  ), убывает (при
), убывает (при  и тем более при
и тем более при  ) и
) и  ; для сходимости исследуемого ряда можно использовать интегральный признак.
; для сходимости исследуемого ряда можно использовать интегральный признак.
Ответ:  .
.
4. Введем новую неизвестную функцию