Выбор наиболее значимых качеств для материалов женского зимнего пальто. К материалам предъявляется сложный комплекс требований эстетического, технического и экономического характера, включающий весьма значительный перечень показателей качества.
Для оценки качества и пригодности материала для изделий определенного назначения и в зависимости от условий их эксплуатации возникает необходимость выбора или уточнения номенклатуры показателей ее свойств. В оценочный комплекс должны быть включены такие показатели, каждый из которых необходим, а всех их вместе достаточно для того, чтобы судить о возможности использования продукции для данного назначения. В настоящее время для этой цели широко используют экспертный метод оценки значимости показателей качества – это способ вынесения суждения, использующий обобщенный опыт и интуицию специалистов (ГОСТ 235554.1-79); экспертная оценка проводится только для материалов верха.
Этот метод состоит из следующих этапов:
1. составляется предварительный перечень показателей на основании литературных источников.
2. формируется экспертная группа на базе специалистов (от 5 до 10 человек).
3. составляются анкеты, содержащие предварительный перечень показателей.
4. анкетирование.
5. обработка результатов анкетирования.
Каждому эксперту предлагается анкета, в которой он оценивает каждую предложенную характеристику соответствующим рангам. Наиболее важной присваивается ранг R = 1, следующему – ранг 2 и т. д. Возможно одинаковые оценки двух или более показателей, например: 3 и 4 показатели равнозначны, в этом случае им дается дробный ранг 3,5 для каждого показателя, т. е сумма ранговых оценок всех показателей должна оставаться постоянной для каждого эксперта.
∑Rij = 1+2+…+n=n(n+1)/2,
где n – число показателей.
Результаты опроса экспертов записываются в табл. 3, для использования в расчетах коэффициентов значимости отдельных характеристик и степени согласованности ранговых оценок.
Сумма ранговых оценок по вертикали Sj для каждой характеристики свойств Х рассчитывается по формуле:
Sij = ∑Rji Pji, для j = 1…..n и используется для сравнительной оценки значимости этих характеристик в пределах табл. 3.
Относительную значимость отдельных свойств удобнее оценивать коэффициентом значимости,
γ = 
Из всех n характеристик выделяют наиболее значимые характеристики no, для которых jl>1/n. Для каждой из выделенных характеристик определяют относительный коэффициент значимости по формуле:
γjo = 
где  – сумма рангов для каждой оставленной характеристики.
– сумма рангов для каждой оставленной характеристики.
Относительную весомость 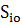 оставленных характеристик рассчитывают по формуле:
оставленных характеристик рассчитывают по формуле:
γjo= 
где  - наименьший (минимальный) из коэффициентов значимости для наиболее значимых характеристик.
- наименьший (минимальный) из коэффициентов значимости для наиболее значимых характеристик.
Для определения согласованности экспертных оценок по данным ранговых оценок экспертов рассчитывается коэффициент согласия (конкордации) по формуле:
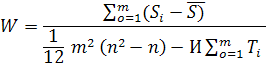
где И – число оценок с одинаковым рангом, S – средняя сумма рангов всех характеристик, равная
S = 
В случае одинаковых оценок разных характеристик свойств отдельными экспертами, при расчете коэффициента конкордации учитывают значение Тi по формуле:
Тi = 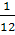 ∑ (ti3 – ti),
∑ (ti3 – ti),
где ti – число оценок с одинаковым рангом в каждой такой группе.
Для оценки значимости коэффициента согласия находят критерий Пирсона Х2 = Wm (n – 1), который сопоставляют с табличными значениями при степени свободы S = n – 1.
Определение наиболее значимых характеристик свойств материалов приводится по каждой группе требований, кроме общих (стандартных).
Коэффициенты значимости, полученные в результате экспертной оценки, проставляют по каждой группе характеристик.
Задание – выбор материалов на женское зимнее пальто.
Экспертов (m) – 10 человек.
Предложено к оценке (Xj) – 10 показателей качества (Xj = 1+10) группы конструкторско-технических требований.
Х1 – усадка;
Х2 – осыпаемость;
Х3 – раздвигаемость;
Х4 – прорубаемость иглой;
Х5 – разрывное удлинение;
Х6 – толщина материала;
Х7 – остаточная циклическая деформация;
Х8 – драпируемость;
Х9 – тангенциальное сопротивление;
Х10 – несминаемость.
Ранговые оценки Rij характеристик свойств материала Xj, коэффициенты согласия (конкордации), W значимости (критерий Пирсона) Х2.
Таблица 3. Ранговые оценки характеристик свойств материала
| Шифр экспертов Ri | Ранговые оценки | 
| Tj | |||||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | Х9 | Х10 | |||
| Sij | ||||||||||||
| γj | 0.149 | 0.014 | 0.095 | 0.02 | 0.151 | 0.035 | 0.089 | 0.182 | 0.184 | 0.087 | ||
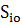
| ||||||||||||
| γjo | 0,175 | 0.112 | 0.177 | 0.104 | 0.214 | 0.217 | ||||||
| ∆i=Si-S | -22 | -23 | -37 | -38 | ||||||||
| ∆i2=(Sj-S)2 |
Расчет показателей таблицы 3.
S1 =4+3+3+4+2+4+3+2+4+4=33
Далее аналогично суммируются ранговые оценки по каждому свойству.
γ1=(10*10-33)/(10*102-10*55)=67/450=0.149
γ2==(10*10-94)/(10*102-10*55)=6/450=0.014
и так далее (см. результаты в табл. 3)
Наиболее значимыми следует считать характеристики со значениями Х1,3,5,7,8,9.
Заполняется строчка суммы ранговых оценок наиболее значимых свойств Sio.
Определяется контрольная сумма по строке.
Sio=33+57+32+60+18+17=217
Определяется относительный коэффициент значимости каждой из выделенных характеристик:
γ1.0=(10*10-33)/(10*10*6-10*217)=67/383=0.175
γ6.0==(10*10-57)/(10*10*6-10*217)=43/383=0.112 и так далее (см. результаты в табл. 3)
Определяется отклонение суммы ранговых оценок от средней величины по каждому свойству: S1 – S = 33 – 55 = - 22 и т. д. (см. результаты в табл. 3)
Определяется контрольная сумма ∑(Sj – S)2 = 7549.
Определяется коэффициент согласия (конкордации):
W=7549/(1/12*102*(102-10))=7549/ 8250=0.915
Значимость коэффициента согласия определяется:
Х2=0.915*10(10-1)=82.35
Полученный критерий Пирсона сравнивается с табличным при степени свободы (n-1)=9X2табл=16,9, что <Xфакт.= 82.35т.е. данный вариант оценки значимости свойств при вероятности 0,95 достоверен.
Таблица 4. Критерий Пирсона
| q | X2табл. при (n-1), равен | ||||||||||
| 0,01 | 6,6 | 9,2 | 11,3 | 13,3 | 15,1 | 16,8 | 18,5 | 20,1 | 21,7 | 23,9 | 24,7 |
| 0,05 | 3,8 | 6,0 | 7,8 | 9,5 | 11,1 | 12,6 | 14,1 | 15,5 | 16,9 | 18,3 | 19,7 |