Перестановки и подстановки

Факультет Кибернетики

Кафедра Автоматизированных систем

 

 

Носырева Л.Л.

 

ДИСКРЕТНАЯ МАТЕМАТИКА

 

Конспективный материал к лекциям

(рабочий вариант)

 

Для специальностей АСУ, МЭИ, ИП, АСОК

 

 

Часть 2

Комбинаторика

 

 

Иркутск 2006

 

 

Комбинаторика

Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Поэтому целями комбинаторного анализа являются изучение комбинаторных конфигураций, алгоритмов их построения, оптимизация таких алгоритмов, а также решение задач перечисления. Простейшими примерами комбинаторных конфигураций являются перестановки, размещения, сочетания и разбиения. При подсчете комбинаторных конфигураций используются правила суммы, произведения и степени.

§ 5.1.

Перестановки и подстановки

Пусть дано множество М = {a₁,a₂,...,a_n}. Перестановкой элементов множества М называется любой кортеж (a_i1,a_i2,...,a_in), состоящий из n различных элементов множества М.

Перестановки отличаются друг от друга только порядком входящих в них элементов. Покажем, что число Р_n всех перестановок множества М равно n!. Действительно на первое место в кортеже можно поставить любой из n элементов, на второе место – любой из n-1 оставшихся и т.д. Для последнего места остается единственный элемент. Поэтому получаем всего n(n-1)(n-2)…2·1 = n! перестановок.

Пример 5.1.1. 1. Расставить на полке 10 книг можно Р₁₀ = 10! = 3 628 800 различными способами.

2. Список студентов группы, состоящей из 25 человек, можно составить Р₂₅ = 25! способами.

Напомним, что биекция σ: М ↔ М называется подстановкой множества М. Пусть σ – подстановка множества М = {1,2,…,n}. Тогда σ(k) = s_k, где 1 ≤ s_k ≤ n, k = 1,2,…, n, { s₁, s₂,...,s_n } = {1,2,..., n }, и поэтому подстановку σ можно представить в виде матрицы, состоящей из двух строк:

Ясно, что если в матрице [σ] переставить столбцы, то полученная матрица будет также определять подстановку σ. Множество всех подстановок множества {1,2,..., n } обозначается через S_n. для подстановок σ,τ S_n можно определить произведение σ · τ как произведение двух функций. Зная матрицы подстановок

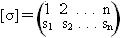
и [τ], переставив столбцы матрицы [τ] так, чтобы её первая строка совпала со второй строкой матрицы [σ]

 

получаем

Теорема 5.1.1. Алгебра ( S_n, ·) является группой. При n ≥ 3 она не коммутативна.

Д о к а з а т е л ь с т в о. Операция – ассоциативна как операция произведений функций. Легко проверяется, что существует единичная подстановка ε с матрицей

и для любой подстановки σ с матрицей 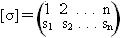существует обратная подстановка σ ^-1, соответствующая матрице .

Если n ≥ 3, то рассмотрим подстановки σ и τ с матрицами и .

Имеем , , 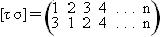т.е. σ τ ≠ τ σ. Таким образом, группа (S_n, ·) некоммутативна.

Группа (S_n, ·) называется симметрической группой степени n. Число элементов этой группы |S_n | равно Р_n = n!.

Подстановка σ называется циклом длины r, если матрицу [σ] перестановкой столбцов можно привести к виду

Очевидно, что в этом случае σ задает биекцию, в которой s₁ → s₂, s₂ → s₃,... s_r→s₁, а остальные элементы неподвижны. Описанный цикл σ обозначается через (s₁ s₂... s_r).

П р и м е р 5.1.3. Подстановка с матрицей является циклом (2536), а подстановка с матрицей циклом не является, так как из неё можно выделить два цикла (14) и (2563).

Циклы (s₁ s₂...s_r) и (t₁ t₂...t_p) называются независимыми, если {s₁,s₂,...,s_r}∩{t₁,t₂,...,t_p} = Ø.

Теорема 5.1.2. Каждую подстановку можно однозначно (с точностью до порядка сомножителей) представить в виде произведения независимых циклов.

В примере 5.1.3. имеем , а .

Двухэлементный цикл (i j) называется транспозицией. При транспозиции i-й и j-й элементы меняются местами, а остальные сохраняют свое положение.

Теорема 5.1.3. Каждая подстановка есть произведение транспозиций.

Д о к а з а т е л ь с т в о. По теореме 5.1.2. достаточно установить, что любой цикл (s₁ s₂...s_r) можно представить в виде произведения транспозиций, но легко проверяется, что (s₁ s₂...s_r) = (s₁ s₂)(s₁ s₃)…(s₁ s_r).

П р и м е р 5.1.4. (1234)=(12)(13)(14).

 

Размещения и сочетания

Пусть М – множество, состоящее из n элементов, m ≤ n. Размещением из n элементов по m или упорядоченной (n,m)- выборкой, называется любой кортеж (а_i1,a_i2,…,a_im), состоящий из m попарно различных элементов множества М. Размещение можно рассматривать как разнозначную функцию f: {1,2,...,m}→M, для которой f(j) = a_ij.

П р и м е р 5.2.1. Для множества М = {a,b,c} пары {a,b} и {b,a} являются размещениями из 3 по 2, тройка (a,c,b) – размещением из 3 по 3, а тройка (b,a,b) размещения не образует.

Число размещений из n по m обозначается через A^m_n или P(n,m). Покажем, что

(5.1)

(напомним, что 0!=1). Действительно, размещение m элементов можно представить как заполнение некоторых m позиций элементами множества М. При этом первую позицию можно заполнить n различными способами. После того как 1-я позиция заполнена, элемент для заполнения 2-й позиции можно выбрать (n-1) способами. Если продолжить этот процесс, то после заполнения позиций с 1-й по (m-1)-ю будем иметь (n-m+1) способов заполнения последней, m-й позиции. Перемножая эти числа, получаем формулу (5.1).

П р и м е р 5.2.2. Из десяти книг произвольным образом берутся и ставятся на полку одна за другой 3 книги. Имеется А₁₀³ вариантов расстановок, где

Сочетанием из n элементов по m или неупорядоченной (n,m)- выборкой, называется любое подмножество множества М, состоящее из m элементов.

П р и м е р 5.2.3. Если М= {a,b,c}, то {a,b}, {a,c}, {b,c} – все сочетания из 3 по 2.

Число сочетаний из n по m обозначается через С_n^m, (_mⁿ) или С(n,m).

Если объединить размещения из n элементов по m, состоящие из одних и тех же элементов (не учитывая порядка их расположения), в классы эквивалентности, то можно установить биекцию φ между сочетаниями и полученными классами по следующему правилу: φ({a_i1,a_i2,...,a_im }) ↔{(b₁,b₂,...,b_m)|{ b₁,b₂,...,b_m }={a_i1,a_i2,...,a_im }}. Так как из каждого сочетания С можно получить m! Размещений (упорядочивая элементы из множества С m! способами по числу перестановок множества С), то каждый класс эквивалентности содержит m! размещений и, значит, А_n^m = m! C_n^m, т.е.

Таким образом,

П р и м е р 5.2.4. Из десяти чисел четыре можно выбрать

Число С_n^m обладает следующими свойствами:

1) С_n^m = C_n^n-m;

 

2) С_n^m + C_n^m+1 = С_n+1^m+1;

 

 

В силу последнего свойства числа С_n^m называют биномиальными коэффициентами.

П р и м е р 5.2.5. Из свойства 3 следует, что