Незнамова Екатерина
Быргазова Наталия
Элементы теории соединений (сочетания, перестановки, размещения с повторениями и без повторений). Бином Ньютона.
Комбинаторика (теория соединений) занимается различного вида соединениями, которые можно образовать из элементов конечного множества.
Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.
Правило суммы
Если элемент А может быть выбран из данного множества n способами, и после этого элемент В может быть выбран m способами, то выбор элемента А или В может быть сделан (n+m) способами.
Пример 1:
Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение:
Данное множество – множество всех тем по алгебре и геометрии.
Обозначим: элемент А – выбранная тема по алгебре, В – выбранная тема по геометрии, т.е. выбрать тему по алгебре можно 17-ю способами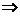 
n=17, а выбрать тему по геометрии – 13-ю способами 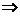m=13.
по правилу суммы: n+ m =17+13=30 тем.
Пример 2:
Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать
а) один билет из спортлото или автомотолотереи?
б) один билет из денежно-вещевой лотереи или автомотолотереи?
в) один билет из денежно-вещевой лотереи, спортлото или автомотолотереи?
Решение:
Обозначим:
Д-В – элемент А, n=5;
Сп. – элемент В, m=6;
Ав. – элемент С, k=10.
а) денежно-вещевая лотерея в выборе не участвует, то по правилу суммы m+ k = 6+10=16.
б) билеты спортлото в выборе не участвуют, тогда n + k = 5+10=15.
в) участвуют все билеты, т.е n + m + k=6+5+10=21.
Правило произведения
Если элемент A можно выбрать n способами из указанного множества, и после этого элемент B может быть выбран m способами, то выбор пары А и В может быть сделан (n 
m) способами.
Пример 3:
В книжном шкафу на двух полках стоят книги. На первой полке – 5 книг, а на второй – 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй?
Решение: Книгу с первой полки можно выбрать 5-ю способами, т.е. n=5, книгу со второй полки можно выбрать 10-ю способами, т.е. m=10. Для ответа на вопрос задачи воспользуемся правилом произведения.
5 10=50 способов.
Пример 4:
В лотерее каждому участнику даётся трёхзначный номер от 000 до 999. Организаторы лотереи решили, что выигрышными будут те номера, в которых есть хоть одна восьмерка. Сколько будет невыигрышных номеров?
Решение:
Первую цифру числа можно записать 9-ю способами, т.к. без восьмёрки 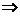n=9. Вторую и третью цифры числа можно также записать 9-ю способами 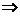m=9, k=9. Воспользуемся правилом произведения
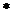m n k=9 9 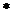9=729 проигрышных номеров.
Пример 5:
В букинистическом магазине лежат 6 разных изданий романа И.С. Тургенева «Рудин», три издания его же романа «Дворянское гнездо» и четыре издания романа «Отцы и дети». Кроме того, есть 5 разных сборников, в каждом из которых есть романы «Рудин» и «Дворянское гнездо», и 7 сборников с романами «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?
Решение:
Рудин – 6.
Дв. гнездо – 3
От. и дети – 4
- 5 изд
- 7 изд.
Воспользуемся правилами суммы и произведения:
6∙3∙4 + 5∙4 + 6∙7=72+20+42=134
Упорядоченные и неупорядоченные выборки
Имеется множество, содержащее n элементов. Из этого множества выбрано m элементов.
Выбор может производиться с возвращением и без возвращения.
Выборки могут быть упорядоченными или неупорядоченными.
Выбор без возвращения.
1) В упорядоченных выборках важно, какие элементы их составляют, и в каком порядке они расположены. Упорядоченные выборки называются размещениями.
Число размещений из n по m – А 
А = 
(1)
Пример:
Сколько можно образовать различных четырехзначных чисел, чтобы цифры не повторялись?
(0,1,2,3,4,5,6,7,8,9)
n=10, m=4
Считаем число размещений, так как важен в каком порядке выбираются цифры:
2) Частным случаем размещений являются перестановки. Они содержат одинаковый набор элементов и отличаются лишь порядком этих элементов.
Число перестановок - 
(2)
Пример 6:
Сколько трехзначных чисел можно составить из цифр (1;6;8), чтобы цифры не повторялись?
Решение:
Считаем число перестановок, так как из 3х элементов выбираем 3:
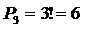
3) Неупорядоченными называются выборки, в которых порядок расположения не важен, а важно лишь какие элементы составляют выборку. Неупорядоченные выборки называются сочетаниями.
Число сочетаний из n по m - 
(3)
или 
(4)
Пример 7:
В группе 10 человек. Нужно выбрать трех человек на одну и ту же должность. Сколько существует способов для выбора?
Решение:
Находим число сочетаний из 10 по 3(т.к. порядок не важен):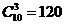 
способов.
Свойства сочетаний
ü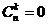 
, если n<k или k<0;
ü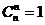 
, 
;
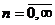ü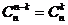 
;
ü Рекуррентная формула (выражает следующее через предыдущее)
, 
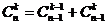Задания
1. Имеются 5 красок. Сколько существует способов для
а) выбора трех красок;
б) раскрашивания трехцветного полосатого флага с заданным направлением полос;
в) для раскрашивания трехцветного флага с заданным направлением полос, если одна полоса должна быть красной?
Решение:
а) Находим число сочетаний из 5 по 3 (т.к. порядок не важен)
способов.
б) Находим число размещений из 5 по 3 (т.к. важен порядок)
способов
в)
или 
или 
Находим в каждом случае число размещений из 4 цветов (т.к. пятый уже занят – красный) по 2 (т.к. цвет третьей полосы уже известен). А затем сложим их.
способов в каждом случае.
12+12+12=36 способов.
2. В группе 7 юношей и 5 девушек. Сколько существует способов для выбора 6 человек, чтобы среди них было не менее 4-х юношей.
Решение:
ю ю ю ю д д или
ю ю ю ю ю д или
ю ю ю ю ю ю
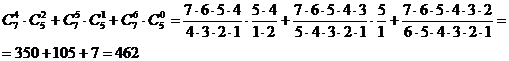
3. Среди 10 команд разыгрывается 3 комплекта медалей: золото, серебро, бронза. Сколько существует способов распределения?
Решение:
Находим число размещений из 10 по 3 (т.к. важен порядок):
Бином Ньютона
Выбор с возвращением