Цель: спроектировать вертикальный стальной резервуар (РВС).
Дано. 1. Объем резервуара – 20 тыс. м3.
2. Плотности нефтепродукта – 900 кг/м3.
3. Место строительства – Сургут.
Задание
1. Определить геометрические параметры резервуара.
2. Определить толщину всех поясов стенки резервуара.
3. Рассчитать стенку резервуара на устойчивость.
4. Выполнить расчет несущего каркаса и настила сферической
крыши.
5. Выполнить графическую часть:
– общий вид резервуара на основании;
– сечение и развертку стенки резервуара. Примеры горизонтальных и вертикальных сварных швов, соединение стенки резервуара и днища;
– общий вид днища. Соединение центральной части, окраек и периферийных листов;
– общий вид сферической крыши резервуара. Узлы соединения главной балки и опорного кольца, главной балки и центрального щита, главных балок и балок настила.
1. Определение геометрических параметров резервуара
Выбор размеров стального прокатного листа для изготовления
стенки
Размеры листа. В соответствии с рекомендациями ПБ 03-605-03
для изготовления стенки выбираем стальной лист с размерами в поставке 2000 × 8000 мм. С учетом обработки кромок листа с целью получения правильной прямоугольной формы при дальнейших расчетах принимаются следующие его размеры 1990 × 7990 мм.
Сначала выбираем высоту резервуара. Для этого используем рекомендации ПБ 03-605-03 (табл. 4.2). В соответствии с этими рекомендациями предпочтительная высота резервуара от 12 до 20 м.
Высота резервуара. Для резервуара объемом 
принимаем номинальную высоту резервуара 
. Соответственно количество поясов в резервуаре будет равно восьми (
). Точная высота резервуара
.
Предварительный радиус резервуара. Радиус резервуара определяется из формулы для объема цилиндра:
|
|
,
Периметр резервуара 
и число листов в поясе 
.
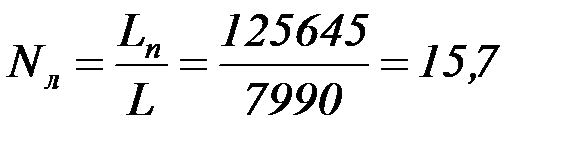Предпочтительней округлять число листов (рис. 4.22) в поясе до целого или выбирать последний лист равным половине длины листа.
Принимаем число листов в поясе 
. Тогда периметр резервуара
,
а окончательный радиус
.
Уточненный объем резервуара.
.
Рис. 4.22. Развертка и сечение стенки вертикального резервуара
2. Определение толщины стенки резервуара
Определение методики и параметров, необходимых для расчета
Минимальная толщина листов стенки резервуара РВС для условий эксплуатации рассчитывается по формуле
,
где 
– коэффициент надежности по нагрузке гидростатического давления;
– коэффициент надежности по нагрузке от избыточного давления и вакуума;
– плотность нефти, кг/м3;
– радиус стенки резервуара, м;
– максимальный уровень взлива нефти в резервуаре, м;
– расстояние от днища до расчетного уровня, м;
– нормативная величина избыточного давления;
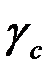– коэффициент условий работы, 
для нижнего пояса, 
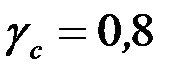для остальных поясов;
– расчетное сопротивление материала пояса стенки по пределу текучести, Па.
Расчетное сопротивление материала стенки резервуаров по пределу текучести определяется по формуле (4.10):
,
где 
– нормативное сопротивления растяжению (сжатию) металла стенки, равное минимальному значению предела текучести, принимаемому
по государственным стандартам и техническим условиям на листовой прокат;
– коэффициенты надежности по материалу;
, так как объем резервуара более 10 000 м3.
|
|
Стенка резервуара относится к основным конструкциям подгруппы «А», для которых должна применяться сталь класса С345 (09Г2С-12) с нормативным расчетным сопротивлением 
.
Вычисляем расчетное сопротивление:
.
Вычисление предварительной толщины стенки для каждого пояса резервуара
Для вычисления используем формулу (4.9), в которой, начиная со второго пояса, единственным изменяемым параметром при переходе от нижнего пояса к верхнему является координата нижней точки каждого пояса
, (4.69)
где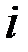 
– номер пояса снизу вверх;
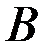– ширина листа.
Основные геометрические размеры резервуара при проведении прочностных расчетов округляем в большую сторону до номинальных размеров так, чтобы погрешность шла в запас прочности: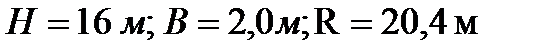 
.
Толщина первого пояса определяется при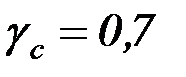 
; 
;
: 
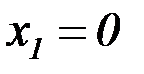Для второго пояса при 
, 
Для остальных поясов резервуара полученные значения для толщины стенки приведены в табл. 4.12.
Таблица 4.12
Толщина стенки поясов резервуара
| Номер пояса | Толщина стенки, мм | Номер пояса | Толщина стенки, мм |
| 15,0 | 6,7 | ||
| 11,5 | 5,0 | ||
| 9,9 | 3,4 | ||
| 8,3 | 1,8 |
Выбор номинального (окончательного) размера толщины стенки.
Значение минимальной толщины стенки для условий эксплуатации увеличивается на величину минусового допуска на прокат и округляется до ближайшего значения из сортаментного ряда листового проката. Полученное значение сравнивается с минимальной конструктивной толщиной стенки 
, определяемой по табл. 4.4.
В качестве номинальной толщины 
каждого пояса стенки выбирается значение большей из двух величин, округленное до ближайшего значения из сортаментного ряда листового проката:
|
|
где 
– припуск на коррозию, мм;
– значениеминусовогодопускана толщину листа, мм;
– минимальная конструктивная толщина стенки.
Величину минусового допуска определяют по предельным отклонениям на изготовление листа. Соответствующие предельные отклонения по толщине листа приводятся в табл. 4.5.
Припуск на коррозию элементов резервуара представляется заказчиком (в курсовом проекте припуск на коррозию необходимо выбирать
2–3 мм).
В табл. 4.13 приводятся все данные для выбора номинального размера толщины стенки.
Таблица 4.13
Номинальная толщина стенки
| Номер пояса |  , мм
| , мм
|  , мм
| + +
|
| 
|
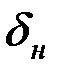
| 15,0 | 2,0 | 0,45 | 17,45 | 11,0 | 18,0 | |
| 11,5 | 13,95 | 14,0 | ||||
| 9,9 | 12,35 | 13,0 | ||||
| 8,3 | 10,75 | 11,0 | ||||
| 6,7 | 9,15 | 11,0 | ||||
| 5,0 | 7,45 | 11,0 | ||||
| 3,4 | 5,85 | 11,0 | ||||
| 1,8 | 4,25 | 11,0 |
3. Расчет стенки резервуара на устойчивость
Проверка устойчивости стенки резервуара производится по формуле (4.13):
,
где 
– расчетные осевые напряжения в стенке резервуара, МПа;
– расчетные кольцевые напряжения в стенке резервуара, МПа;
– критические осевые напряжения в стенке резервуара, МПа;
– критические кольцевые напряжения в стенке резервуара, МПа.
Осевые напряжения определяются по минимальной толщине стенки пояса, кольцевые напряжения – по средней толщине стенки.
Расчетные осевые напряжения для резервуаров РВС определяются по формуле (4.14)
,
где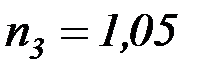 
– коэффициент надежности по нагрузке от собственного
веса;
– коэффициент надежности по снеговой нагрузке;
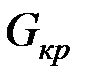– вес покрытия резервуара, Н;
– вес вышележащих поясов стенки, Н;
– полное расчетное значение снеговой нагрузки на горизонтальную проекцию покрытия, Н;
– вес покрытия резервуара, Н;
– расчетная толщина стенки i-го пояса резервуара, м.
Определение веса крыши
Вес покрытия резервуара рассчитывается по нормативному давлению крыши 
(табл. 4.6)
.
Для резервуара объемом давление крыши 
.
.
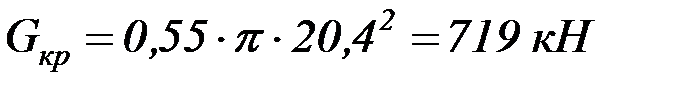Определение веса стенки резервуара
Вес вышележащих поясов стенки резервуара определяется из условия, что высота всех поясов одинакова и равна ширине листа :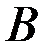
,
где 
– номер последнего пояса, если начало отсчета снизу;
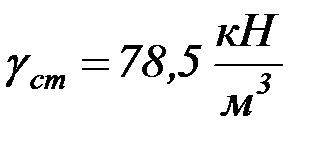– удельный вес стали.
Вес стенки при расчете первого пояса
.
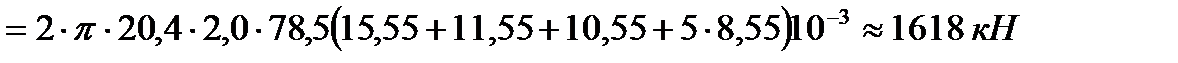Вес стенки при расчете второго пояса
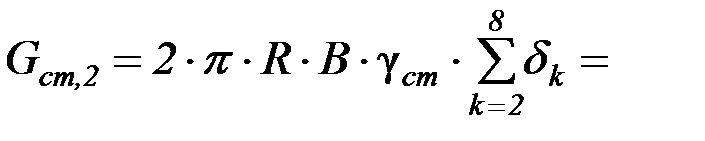
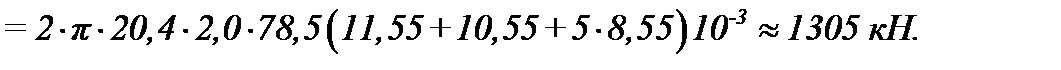
Результаты расчетов веса стенки для всех поясов приведены в табл. (4.14).
Таблица 4.14
Вес стенки резервуара
| Номер пояса | Вес стенки  , кН
| Номер пояса | Вес стенки , кН
|
Определение снеговой нагрузки
Нормативная снеговая нагрузка на горизонтальную проекцию резервуара
где 
– коэффициент перехода от веса снегового покрытия горизонтальной поверхности земли к снеговой нагрузке на трубопровод;
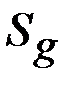– нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли, которое выбирается по СниП 2.01.07-85 (табл. 4.7) для соответствующего снегового района Российской Федерации.
Город Сургут находится в IV снеговом районе, для которого
=2,4 кН. Коэффициент 
для такого варианта крыши, когда угол наклона поверхности крыши к горизонтальной плоскости 
.
Вес снегового покрова на всю крышу
.
Определение нагрузки от вакуума
Нормативная нагрузка от вакуума на покрытие определяется как
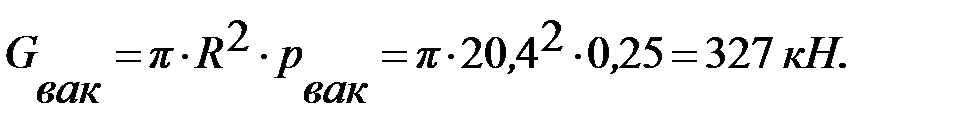
Определение осевых напряжений в каждом поясе стенки резервуара от вертикальной нагрузки
Определение напряжений:
– в первом поясе
;
– во втором поясе
.
Значения осевых напряжений в остальных поясах приведены в
табл. 4.15.
Таблица 4.15
Напряжения для расчета стенки резервуара на устойчивость
| Номер пояса |  , МПа
|  , МПа
| 
| , МПа
| , МПа
| 
| +
|
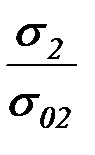
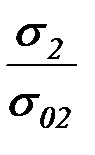
| 3,4 | 10,4 | 0,33 | 1,2 | 1,6 | 0,75 | 1,08 | |
| 4,4 | 7,7 | 0,57 | 1,32 | ||||
| 4,6 | 7,0 | 0,66 | 1,41 | ||||
| 5,5 | 5,7 | 0,96 | 1,71 | ||||
| 5,3 | 5,7 | 0,93 | 1,68 | ||||
| 5,2 | 5,7 | 0,91 | 1,66 | ||||
| 5,0 | 5,7 | 0,88 | 1,63 | ||||
| 4,8 | 5,7 | 0,84 | 1,59 |
Определение осевых критических напряжений
Осевые критические напряжения определяются по формуле (4.20)
,
где 
МПа – модуль упругости стали;
– коэффициент, принимаемый по табл. 4.8.
Для определения коэффициента необходимо вычислить среднюю толщину стенки
.
Вычисляем отношение радиуса резервуара к средней толщине стенки: 
По табл. 4.10 выбираем коэффициент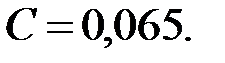 
Вычисляем осевые критические напряжения:
– для первого пояса
;
– для второго пояса
.
Остальные значения критической силы приведены в табл. 4.15.
Определение кольцевых напряжений
Расчетные кольцевые напряжения в стенке при расчете на устойчивость резервуара определяются по формуле (4.22).
,
где 
– нормативное значение ветровой нагрузки на резервуар, Па;
–коэффициент надежности по ветровой нагрузке;
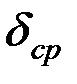–средняя арифметическая толщина стенки резервуара, м.
Нормативное значение ветровой нагрузки определяется по формуле (4.23)
,
где 
– нормативное значение ветрового давления, для рассматриваемого района, Па;
– коэффициент, учитывающий изменение ветрового давления по высоте;
– аэродинамический коэффициент.
Сургут относится ко второму району по давлению ветра (табл. 4.9), соответственно из таблицы выбираем 
.
Коэффициент 
для резервуаров высотой от 10 до 20 метров.
Аэродинамический коэффициент выбирается по СНиП 2.01.07-85 «Нагрузки и воздействия» (табл. 4.10).
Вычисляем отношение
.
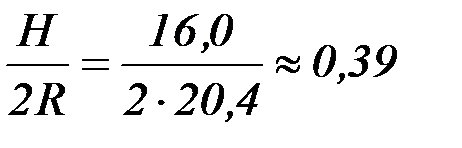Выбираем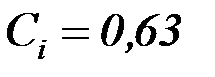 
по таблице с использованием метода линейной интерполяции.
Вычисляем ветровую нагрузку (давление):
.
Вычисляем кольцевые напряжения:
.
Критические кольцевые напряжения определяются по формуле (4.24)
,
где 
– геометрическая высота стенки резервуара, м.
.
Если по результатам расчета условие устойчивости не выполняется, то значения номинальной толщины стенки для соответствующих поясов стенки резервуара должны быть увеличены.
4. Расчет сопряжения стенки резервуара с днищем
Дано:
– коэффициент постели для резервуара, установленного на хорошо уплотненном песчаном основании;
– толщина стенки нижнего пояса;
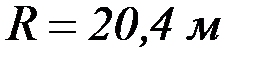– радиус резервуара;
– высота стенки резервуара;
– толщина окрайки днища;
– ширина окрайки днища;
_ давление в нижней точке резервуара.
Определение деформационных характеристик элементов конструкций
Коэффициент постели стенки резервуара
.
Цилиндрическая жесткость стенки
.
Коэффициент деформации стенки
.
Цилиндрическая жесткость днища
.
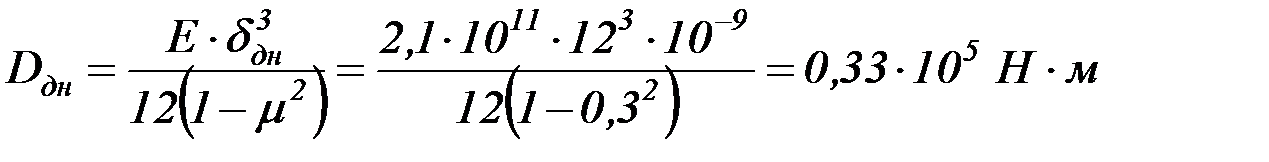Коэффициент деформации днища
.
Функции Крылова
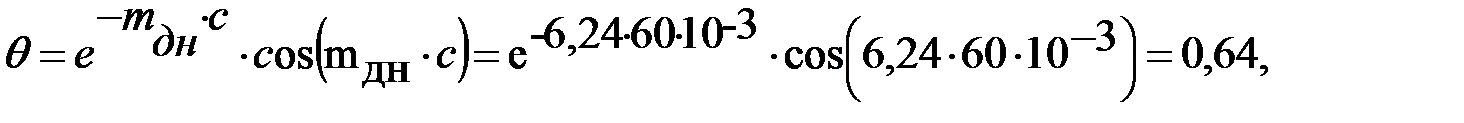
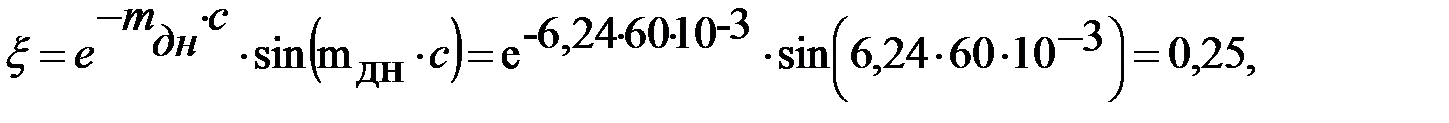
Система канонических уравнений метода сил
В узле сопряжения стенки и днища резервуара (рис. 4.12) неизвестными считаются изгибающий момент 
и сила 
– поперечная для стенки резервуара и продольная для днища. Для их определения составляется система уравнений, характеризующих условие совместности деформаций стенки резервуара и днища:
Определяем коэффициенты и перемещения, входящие в систему уравнений:
;
Решение системы канонических уравнений
Подставляем в систему уравнений полученные коэффициенты и перемещения
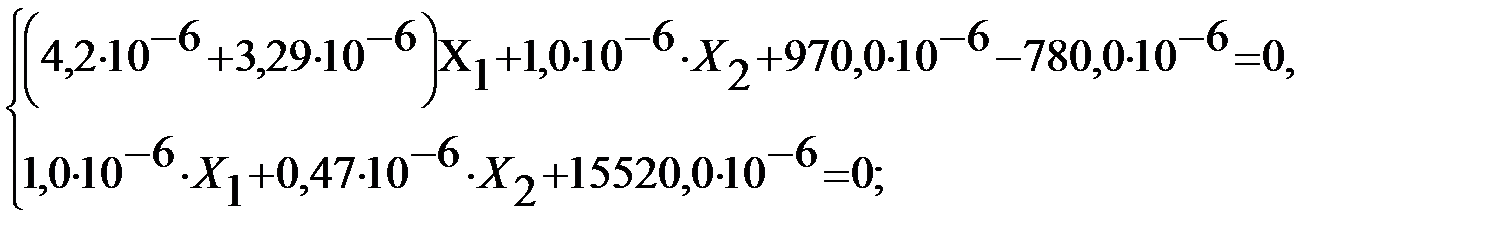
Второе уравнение системы умножим на дробь 
и вычтем из первого:
, откуда 
.
Из первого уравнения системы получаем 
,
.
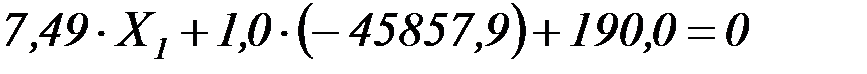Проверка прочности стенки в точке сопряжения с днищем
Проверку прочности стенки выполняем от действия изгибающего момента и продольной сжимающей силы 
(та же величина, что и при расчете на устойчивость нижнего пояса стенки резервуара):
На рис. 4.13 дана расчетная схема для определения напряжений в стенке. Наибольшие значения возникают в точке сложения сжимающих напряжений от изгиба и вертикальной нагрузки.
Изгибающий момент
.
Момент сопротивления изгибаемой стенки
.
Второе слагаемое уравнения – это напряжение в нижней точке первого пояса (табл. 4.15)
.
Расчетное сопротивление для стали нижнего пояса резервуара
.
Выполняем проверку на прочность:
.
Таким образом, условие прочности
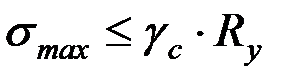выполняется, т.к. 
.
Проверка прочности днища
Проверку прочности днища проводим по напряжениям, возникающим от изгибающего момента 
.
В этом случае момент сопротивления сечения днища
.
Для стального листа окрайки расчетное сопротивление будет такое же, что и для нижнего пояса стенки:
.
Однако максимальные напряжения при изгибе окрайки оказались выше расчетного сопротивления:
.
Для увеличения прочности днища необходимо увеличить толщину окрайки или выбрать материал, у которого расчетное сопротивление будет выше максимальных напряжений.
При толщине окрайки 
,
.
В этом случае условие прочности выполняется, однако следует сделать замечание о том, что для корректного выбора новой толщины днища или стенки необходимо весь расчет повторить.
Проверка сварного шва на прочность
Расчетная схема таврового соединения днища и нижнего пояса стенки резервуара изображена на рис. 4.14. При толщине стенки меньше 20 мм соединение выполняется без разделки нижней кромки стенки. Катет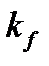 
принимаем равным 12 мм. Коэффициент сварного шва принимается по таблице 34 СНиП II-23-81 «Стальные конструкции» – 
(для ручной электродуговой сварки). Коэффициент условий работы сварного шва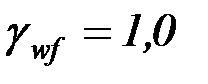 
.
Условие прочности сварного шва:
,
где – сила, срезающая шов по металлу сварного шва;
– длина сварного шва для случая расчета оболочки, когда 
сила, отнесенная к единице длины;
– расчетное сопротивление по металлу сварного шва для электрода 
.
Выполняем проверку сварного шва:
,
.
Поскольку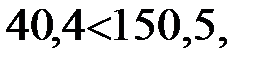 
условие прочности сварного шва выполняется.
5. Пример расчета сферической крыши
Дано:
– радиус цилиндрического резервуара;
– радиус сферической крыши;
– нормативный вес крыши;
– количество главных балок.
Главные балки на расчетной схеме представляем как трехшарнирные арки (рис. 4.23).
Рис. 4.23. Расчетная схема главных балок сферической крыши
в виде трехшарнирной арки
Угол 
зависит от соотношения радиусов и 
:
, 
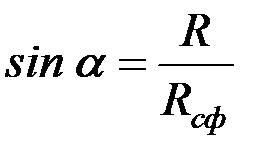Высота купола 
определяется из геометрических соотношений:
Определение нагрузки на главную балку
При симметричной схеме нагружения каждая из главных балок воспринимает ту часть нагрузки, которая приходится на один сектор круговой проекции крыши на горизонтальную плоскость. Количество секторов крыши равно количеству главных балок. В силу геометрических особенностей изменение нагрузки на главную балку от центра крыши до опоры на стенку пропорционально длине дуги, с которой собираются нагрузки (рис. 4.24). Поэтому интенсивность вертикальной нагрузки на главную балку линейно возрастает от нуля в центре до 
в крайних точках при опирании на стенку.
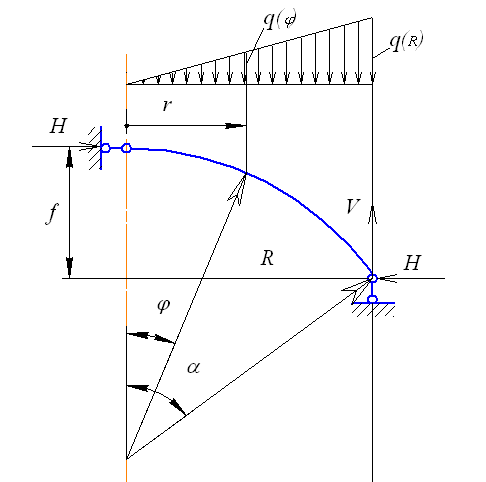
Рис. 4.24. Расчетная схема главной балки сферической крыши
вертикального резервуара
Эпюра нагрузок на главную балку будет полностью определена, если вычислить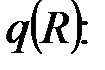 
. (4.70)
;
;
.
.
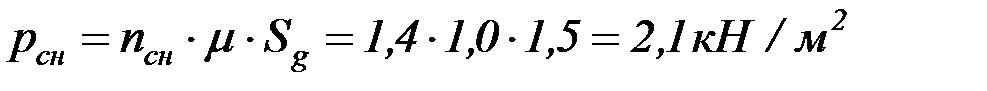Определение реакций опор
Вертикальная реакция 
и распор определяются из уравнений статики.
Сумма проекций сил на вертикальную ось равна нулю:
,
.
Сумма моментов относительно правой опоры равна нулю:
.
Определение изгибающих моментов в поперeчных сечениях главных балок
Уравнение изгибающих моментов записывается как функция от угла 
, определяющего положение поперечного сечения (рис. 4.24):
, (4.71)
.
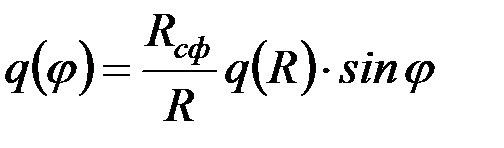Окончательно уравнение принимает вид
. (4.72)
Полученное уравнение позволяет построить эпюру изгибающих моментов 
(рис. 4.25).
Рис. 4.25. Эпюра изгибающего момента в поперечных сечениях главной балки
Однако, для того чтобы проанализировать конструкцию главной балки с целью определения наиболее опасного сечения, необходимо найти координату сечения с наибольшим изгибающим моментом.
Определение максимального изгибающего момента
Для определения максимального изгибающего момента уравнение (4.72) исследуется на экстремум. В результате находим угол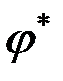 
, определяющий положение сечения, в котором изгибающий момент максимальный. Для определения максимального изгибающего момента находится производная 
и приравнивается нулю:
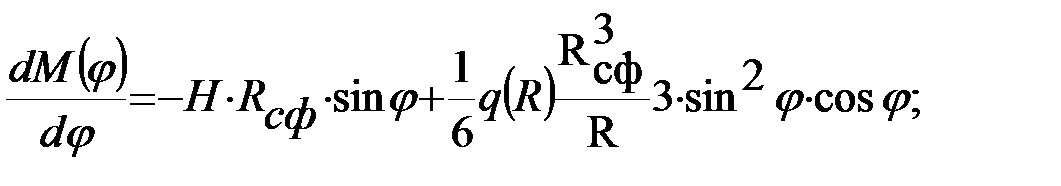(4.73)
;
;
. (4.74)
В результате решения тригонометрического уравнения (4.74) определяется угол 
(4.75)
; 
.
Для определения максимального изгибающего момента значение угла 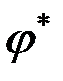подставляется в уравнение (4.72):
. (4.76)
В соответствии с рекомендациями ОАО «Транснефть» каркас стационарной кровли резервуара относится к основным конструкциям резервуара подгруппы А, для которых рекомендуется использовать сталь класса С345 по ГОСТ 27772 (09Г2С-12).
Для стали С345 нормативное расчетное сопротивление .
Условие, выражающее предельное состояние для главной балки:
, (4.77)
где – коэффициент условий работы;
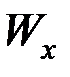– момент сопротивления стандартного прокатного двутаврового сечения.
Расчетное сопротивление стали
,
где 
– коэффициент надежности по материалу;
– коэффициент надежности по назначению.
Из выражения (4.77) определяется значение момента сопротивления 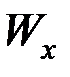, удовлетворяющее условию прочности:
.