для нахождения числа вариантов
В комбинаторике по каждой конкретной задаче составляется своя математическая модель, описывающая данное множество и те наборы элементов, которые надо изучить. Вместо слова «наборы» обычно употребляют термин «выборки» (иногда — «конфигурации», «комбинации» или «соединения»). Две конкретные выборки могут отличаться друг от друга составом или порядком расположения элементов. Каждый тип выборок имеет своё название. Различают три вида комбинаций: размещения, перестановки и сочетания. Рассмотрим их.
ПЕРЕСТАНОВКИ
Предварительно введем новое важное для нас понятие
Произведение всех натуральных чисел от 1 до п обозначают п! (читают: п — факториал).
| п! = 1 · 2 · 3 · 4 · …· (п – 2) · (п – 1) · п 1! = 1 0! = 1 |
Например, 6! = 720, 7! = 5040. Объясните, как получены данные равенства.
Задача 9. Первоклассник Петя решил поставить 3 учебника в ряд на книжной полке. Сколько существует способов расстановки?
Пусть у Пети есть «Математика» (М), «Азбука» (А) и «Окружающий мир» (О). Каждый способ расстановки — это упорядоченный набор из трех книг. Способы расстановки отличаются только порядком расположения книг друг за другом. Возможны всего шесть вариантов расстановки (слева направо): МАО, МОА, АМО, АОМ, ОМА, ПАМ.
А если книжек немного больше, например, десять? Воспользуемся правилом умножения.
Будем считать, что на книжной полке имеются десять ячеек. Тогда в первую ячейку можно поставить любую из десяти книг. Во вторую — любую из оставшихся девяти. В третью ячейку — одну из восьми. И так далее. По правилу умножения получим 10 • 9 • 8 • 7 • 6 • 5 • 4 • 3• 2• 1способов.
Ответом к задаче 9 является 3! = 6. Если книг десять, то ответ равен 10! = 3 628 800.
| В комбинаторике конечное упорядоченное множество называется перестановкой. |
Перестановки элементов одного и того же множества отличаются только порядком расположения элементов друг относительно друга. Когда мы задаем одну (конкретную) перестановку, мы определяем, какой элемент будет первым, какой — вторым, третьим и т. д. Каждому номеру от 1 до п соответствует свой элемент, а каждому элементу — свой номер. Получается взаимно однозначное соответствие.
| Число перестановок из п элементов: Рп = n (n – 1) (n – 1) ×… × 2 × 1 = n! (1.1) |
Задача 10. Сколькими способами 7 партий можно расставить по порядку в избирательном бюллетене?
Каждой партии присваивается номер. Тогда количество вариантов составить избирательный бюллетень равно
7 · 6 · 5 · 4 · 3 · 2 · 1 = 7! = 5040.
Замечание:
Иногда в перестановке один и тот же элемент встречается несколько раз.
Задача 12. Каждую букву слова МАТЕМАТИКА написали на отдельной карточке. Карточки перемешали и снова разложили по порядку. Сколько различных на вид «слов» (считая бессмысленные наборы букв) можно получить, используя сразу все 10 карточек?
В слове математика 10 букв, но буква А встречается 3 раза, буква М – 2 раза, буква Т – 2 раза. Такие повторения называются кратностями. Слово, как и число — упорядоченный набор символов. Запишем на карточки буквы слова МАТЕМАТИКА так М1А1Т1ЕМ2А2Т2ИКА3. Рассмотрим две возможные перестановки букв, записанных на карточке: М1А2Т1ЕМ2А1Т2ИКА3. и М1А1Т1ЕМ2А2Т2ИКА3. Записано слово одно, но перестановки разные. Следовательно, количество перестановок должно уменьшиться во столько раз, сколько существует перестановок из букв А1, А2, А3. Количество перестановок из трех элементов равно 3!, значит, общее количество перестановок букв в слове МАТЕМАТИКА в 3! раз. Аналогичные рассуждения можно повторить и для букв М и Т.
Если решать подобную задачу в общем виде, то можно применять формулу, дающую ответ при подстановке общего количества мест (п) и кратностей (повторений) размещаемых элементов (n1, п2>..., nk}.
 (1.2)
(1.2)
РАЗМЕЩЕНИЯ
Задача 13. На книжной полке осталось место только для трех книг. Сколькими способами можно поставить на эти места 3 книги, выбирая их из 10?
Рассуждаем так же, как в задаче 9. В первую ячейку можно поставить любую из десяти книг. Во вторую — любую из девяти. В третью — любую из восьми оставшихся. Применяя правило умножения, получаем 10 9 8 = 720 способов расстановки.
При таких расстановках мы выбираем три разные книги из десяти (подмножество) и упорядочиваем (размещаем) на трех местах.
| Упорядоченные подмножества данного множества называются «размещениями из п элементов на k мест или проще: размещениями из п по k. |
По-английски размещения называются arrangements, поэтому их число обозначается буквой А.
Число размещений из п элементов на k мecm: (1.3а)
 = n (n – 1) (n – 1)… (n – k +1).
Данную формулу можно записать и так: = n (n – 1) (n – 1)… (n – k +1).
Данную формулу можно записать и так:  = =  (1.3b) (1.3b)
|
Обращаем внимание на то, что в последней скобке стоит выражение (п - k + 1). Дело в том, что количество сомножителей в формуле равно k. A поскольку отсчет сомножителей начинается с нулевого номера — а именно с числа п, то последним в формуле стоит сомножитель (п - k + 1).
В нашей задаче 13 п = 10, k = 3, тогда
 = 10 9 8 = 720
= 10 9 8 = 720
или
 =
=  =
=  =
=  =
=
 = 10 9 8 = 720
= 10 9 8 = 720
Применим формулу размещений для решения следующей задачи.
Задача 14. С колькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется ткань пяти цветов.
Горизонтальные цветные полосы на флаге образуют упорядоченное множество, поэтому количество вариантов можно найти, пользуясь формулой для нахождения числа размещений из п элементов на k мест. Искомое число трехцветных флагов равно  = 5 × 4 × 3 = 60. Ответ: 60 способов.
= 5 × 4 × 3 = 60. Ответ: 60 способов.
Задача 15. В учебной группе 25 студентов. Им необходимо выбрать старосту, профсоюзного лидера и культурного организатора. Сколькими способами может быть сделан этот выбор?
Тройка (староста, профсоюзный лидер, культурный организатор) является упорядоченной тройкой, так как каждый человек в данной тройке выполняет свои функции. Поэтому для решения данной задачи надо найти число размещений из 25 по 3. Подставляем в формулу:  =
=  =25 24 23 = 13800. Ответ: 13800 способов.
=25 24 23 = 13800. Ответ: 13800 способов.
Задача 16. Двенадцать детей делят по жребию три разных игрушки. Каждый получает не более одной. Сколько существует вариантов распределить эти три игрушки по жребию между двенадцатью детьми?
Рассмотрим первую игрушку. В результате жребия она должна оказаться у какого-то ребёнка (12 способов), для второй игрушки — 11 способов из оставшихся, для третьей — 10 способов. По правилу умножения получаем ответ: 12 11 10 = 1320. Значит, это число размещений из 12 по 3.
Ответ: 1320 вариантов.
Размещения с повторениями
Допустим теперь, что в упорядоченном наборе под разными номерами могут стоять одинаковые элементы данного множества.
Задача 17. Сколько различных двухзначных чисел можно составить из цифр 1,2, 3?
Число — это последовательная запись цифр, от перестановки которых число может измениться. Понятно, что на первом месте может стоять любая из трех цифр. И на втором месте может стоять любая из тех же трех цифр, так как цифры в числе могут повторяться. Применяя правило умножения, получаем, что нужных нам чисел девять. Вот все эти числа: 11, 12, 13, 21, 22, 23, 31, 32, 33.
Выборки такого типа называются «размещениями с повторениями».
Число размещений из п элементов на k мecm
(с повторениями):
 (1.4) (1.4)
|
Задача 18. Сколькими способами дни рождения случайных четырёх людей могут размещаться по дням недели?
Каждый из четырех человек может иметь день рождения в любой из семи дней, поэтому всего способов будет равно
7 7 7 7 = 2041. Ответ: 2041 способ.
Задача 19. В группе 25 студентов. Сколькими способами можно распределить а) два различных учебника; б) два различных учебника так, чтобы никто из студентов не получил оба учебника.
Решение а). Для первого учебника имеется 25 претендентов, или 25 способов выбора, для второго учебника – 25 способов выбора, так как никаких ограничений на распределение учебников нет. Тогда по правилу умножения возможны 25 × 25 = 625 вариантов.
Эта задача на размещение с повторениями (выбор совершается с возвращением объекта в прежнюю совокупность)
Решение б) В этом случае есть ограничение: никто из студентов не может получить оба учебника. Тогда для первого учебника – 25 способов выбора, а для второго – 24. Тогда по правилу умножения возможны 25 × 24 = 600 вариантов.
Эта задача на размещение без повторения (выбор совершается без возвращения объекта в прежнюю совокупность).
СОЧЕТАНИЯ
Если задача комбинаторики сводится к подсчету числа способов выбрать из п различных объектов какие-то k объектов без повторений, причем порядок выбора не важен, то применяется специальная формула, рассматриваемая ниже.
В этом случае фактически подсчитывается количество подмножеств с одним и тем же количеством элементов, составленных из заданного множества.
Задача 20. В учебной группе 25 студентов. Необходимо выбрать трех делегатов на студенческую конференцию. Сколько существует разных вариантов делегации?
Если выбирать студентов по порядку, то число вариантов будет равно произведению 25 24 23 (то есть числу размещений из 25 по 3). Но разные способы выбора по порядку могут приводить к одному и тому же результату: выбираются одни и те же три студента (только в разном порядке). Запишем все упорядоченные тройки (25 • 24 23 штук) и сгруппируем те, в которых выбраны одни и те же люди. В каждой группе будет ровно по 3!=6 троек, отличающихся только порядком выбранных людей. Групп будет столько, сколько существует разных составов делегации. Следовательно, если это число умножить на шесть, получится число 25 • 24 • 23. Поэтому число разных составов делегации равно (25 24 23): 6 = 2300.
Ответ: 2300 способов.
| В комбинаторике k-элементное подмножество (т. е. часть) данного n-элементного множества называется сочетанием из п по k элементов. |
Число всех сочетаний из n элементов по m элементов обозначается через  (от первой буквы французского слова combinaison, что означает «сочетание»).
(от первой буквы французского слова combinaison, что означает «сочетание»).
Пользуясь рассуждениями, приведёнными при решении задачи 12, получим формулу для числа сочетаний из п по k элементов.
Число сочетаний из п по k элементов (без повторений):
 = = 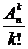 (1.5а) (1.5а)
 = = 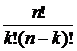 (1.5b) (1.5b)
|
В этой формуле, по определению, 0! = 1. Это используется при п = k или при k = 0.
Чтобы была понятна формула, выпишем все виды сочетаний из множества, состоящего из четырёх букв {a, b, с, d}:
| одно сочетание по четыре из четырёх элементов — {а, b, с, d}; |  = = 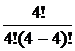 = 1 = 1
|
| четыре сочетания по три из четырёх элементов — {a, b, с} {a, b, d} {a, с, d} {b, c, d}; |  = =  = 4 = 4
|
| шесть сочетаний по два из четырёх элементов — {а, b} {а, с} {a, d} {b, с} {b, d} {с, d}; | 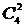 = = 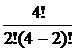 = 6 = 6
|
| четыре сочетания по одному из четырёх элементов — {а} {b} {с} {d}; |  = =  = 4 = 4
|
| одно сочетание, не содержащее ни одного элемента (пустое множество). |  = =  = 1 = 1
|
Решим задачи, пользуясь этими формулами.
Задача 21. Сколько существует способов составить подарочный набор из трех предметов, если имеется восемь различных сувениров?
Три предмета в подарке представляют собой неупорядоченное множество. Неважно, в каком порядке мы уложили предметы в подарок, важно, что их три. Тогда ответ можно получить, применив одну из формул (1.5а) или (1.5b)
 =
= 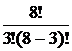 =
=  =
=  = 56.
= 56.
Задачи типа 20 легко распознаются, ответ вычисляется по стандартной формуле (1.5а) или (1.5b). Так, например, из десяти городов выбрать один для проведения олимпиады можно  — десятью способами; из четырех блюд в кафе можно заказать два разных блюда
— десятью способами; из четырех блюд в кафе можно заказать два разных блюда 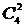 — шестью способами; имея 30 видов новогодних открыток можно составить набор из шести разных открыток
— шестью способами; имея 30 видов новогодних открыток можно составить набор из шести разных открыток  — способами.
— способами.
Всякий раз, применяя формулы (1.5а) или (1.5b), мы подсчитываем количество различных выборок из данного множества, которые отличаются друг от друга только составом, причём состоят из одинакового числа элементов.
Задача 22. Сколькими способами можно в «Спортлото» выбрать 5 номеров из 36?
Искомое число способов:  =
=  =
=  =
=  = 376992.
= 376992.
Задача 23. Восемь человек делят по жребию три равноценных билета в кино. Сколько существует способов распределить эти три билета?
Если способы различаются только тем, кому из восьми людей достанутся билеты, то задача сводится к простому выбору трёх человек из восьми. Поэтому ответ:  = 56.
= 56.
Задача 24. Сколько существует пятизначных натуральных чисел, состоящих из трёх единиц и двух двоек?
Способ 1. Числа различаются положением двоек на пяти местах внутри числа. Поэтому их количество равно числу способов выбрать два места под двойки из пяти, то есть  = 10.
= 10.
Способ 2. Можно решить задачу и по-другому, если будем вести разговор о положении единиц на пяти местах внутри числа. Тогда количество нужных нам пятизначных чисел равно числу способов выбрать три места под единицы из пяти, то есть 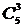 = 10. Ответ: 10 чисел.
= 10. Ответ: 10 чисел.
Задача 25. Сколько существует различных пятизначных чисел, состоящих из двух единиц, двух троек и одной пятёрки?
Для решения этой задачи представим пятизначное число как пять последовательных ячеек (мест) для цифр. Выберем сначала места для единиц. Это можно сделать десятью способами ( =10). Затем из оставшихся трёх мест выберем два места для троек. Это можно сделать тремя способами (
=10). Затем из оставшихся трёх мест выберем два места для троек. Это можно сделать тремя способами ( = 3). Осталось одно место, куда надо поставить пятерку одним способом. Всего, по правилу умножения,
= 3). Осталось одно место, куда надо поставить пятерку одним способом. Всего, по правилу умножения, 
 1 = 30.
1 = 30.
Ответ: 30 чисел.
Сочетания с повторениями
Задача 26. В магазине есть четыре сорта мороженого: пломбир, крем-брюле, фисташковое и шоколадное. В упаковку помещается 6 шариков мороженого. Сколькими способами можно составить такой набор?
Поскольку порядок расположения шариков мороженого в упаковке не важен — речь идет о сочетаниях. Но сорта мороженого в наборе могут, и даже обязательно будут, повторяться. Следовательно, мы имеем новый тип комбинаций, который называется «сочетания с повторениями». Для решения задач такого типа имеется своя формула.
Число сочетаний с повторениями по k элементов, принадлежащих п разным сортам (из п сортов по k элементов):
 =
=  (1.6)
(1.6)
В задаче 26 получаем ответ  = 84.
= 84.
КОМБИНИРОВАННЫЕ ВЫБОРКИ
Задача 27. В колоде — 36 карт: четыре масти по девять карт (от шестёрки до туза). Сколько существует способов составить набор из шести карт так, чтобы в него вошли два короля, три десятки и одна дама?
Это типовая задача на составление так называемой «комбинированной выборки». Исходная совокупность карт (колода) представляет собой смесь разных сортов карт. В нашей задаче важно определить, на какие сорта (классы) надо разбить всю совокупность, чтобы выбор осуществлялся из каждого класса в определенном количестве. Схема рассуждений такова:
1) королей всего четыре, из них берем два, 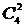 =6 способов
=6 способов
2) десяток всего четыре, из них берем три, способов  =3
=3
3) дам всего четыре, из них берем одну, способов  =4.
=4.
Поскольку требуется сделать выбор и (1), и (2), и (3), то, по правилу умножения, число комбинированных наборов равно 6 3 4 = 72. Ответ: 72 способа.
Задача 28. В колоде — 36 карт: четыре масти по девять карт (от шестёрки до туза). Сколько существует способов составить набор из шести карт так, чтобы в него вошли ровно два короля?
Решение:
1) королей всего четыре, из них берем два, 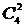 =6 способов;
=6 способов;
2) не королей всего 32, из них берем четыре,  = 35960 способов.
= 35960 способов.
Всего наборов из двух королей и четырех каких-то карт (не королей) = 6 • 35960 = 215760. Ответ: 215760 способов.
Задача 29. В колоде — 36 карт: четыре масти по девять карт (от шестёрки до туза). Сколько существует способов составить набор из шести карт так, чтобы в него вошли два короля и дама пик?
Решение:
1) королей всего четыре, из них берем два, способов 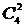 =6;
=6;
2) дама пик одна, способ выбора один;
3) не королей и не дам пик всего 37, из них берем три карты, способов  =4495, всего способов составить набор = 6 • 4495 = 26970. Ответ: 26970 способов.
=4495, всего способов составить набор = 6 • 4495 = 26970. Ответ: 26970 способов.
Задачи типа 27 - 29 легко формализуются. Каждый раз «смесь» разбивается на части (классы), не имеющие общих элементов. Из каждого класса выбираются сочетания, количество сочетаний перемножается. Надо внимательно следить за тем, чтобы комбинированная выборка содержала нужное число элементов, и все они были бы описаны при решении задачи.
Задача 30. В группе 25 человек. Сколькими способами а) их можно поставить в шеренгу на занятии по физкультуре, б) избрать старосту, заместителя и казначея, в) выбрать трех представителей для команды в КВН?
Решения:
а) Р25;
б)  = 25 24 23 = 13800 способов;
= 25 24 23 = 13800 способов;
в)  =
=  =
=  = 375 способов.
= 375 способов.