1. Задача о работе плоского силового поля
Пусть материальная точка М, двигаясь прямолинейно под действием постоянной силы 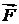 совершает перемещение
совершает перемещение 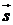 . Работой А, производимой этой силой, называется скалярное произведение вектора силы
. Работой А, производимой этой силой, называется скалярное произведение вектора силы 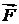 на вектор перемещения
на вектор перемещения 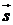 :
:
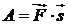 .
.
Если в каждой точке М области (P) определена сила, величина и направление которой зависят только от приложения точки М, то говорят, что на области (P) задано силовое поле.
Пусть материальная точка М движется по кривой ВС, лежащей в области (P) под действием силового поля.
Задача. Определить работу А силового поля при перемещении материальной точки из точки В в точку С по кривой.
Разобьем кривую ВС произвольными точками 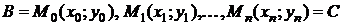 , взятыми по направлению от В к С, на n частичных дуг. На каждой частичной дуге
, взятыми по направлению от В к С, на n частичных дуг. На каждой частичной дуге 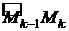 выберем произвольно точки
выберем произвольно точки 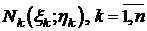 . На частичной дуге
. На частичной дуге 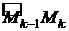 заменимприближенно переменную силу
заменимприближенно переменную силу 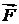 постоянной силой
постоянной силой 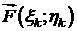 , равной вектору силы
, равной вектору силы 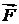 в точке
в точке  . А движение материальной точки по этой дуге заменим ее движением по хорде
. А движение материальной точки по этой дуге заменим ее движением по хорде 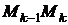 этой дуги.Выполним это все
этой дуги.Выполним это все  . В результате приближенных замен имеем:
. В результате приближенных замен имеем:
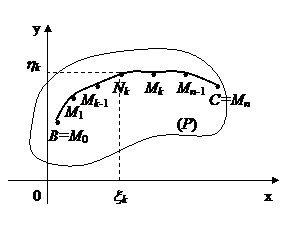 1) материальная точка движется по ломаной, вписанной в кривую ВС;
1) материальная точка движется по ломаной, вписанной в кривую ВС;
2) на каждом звене ломаной на материальную точку действует постоянная сила.
Работа силы 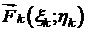 на хорде
на хорде 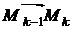 равна
равна
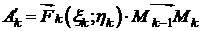 .
.
Суммируя по  , получим
, получим
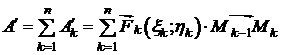 , (1)
, (1)
 - работа ступенчатой силы при движении материальной точки по ломаной
- работа ступенчатой силы при движении материальной точки по ломаной  , вписанной в кривую ВС. Эту работу считают приближением искомой работы А силы
, вписанной в кривую ВС. Эту работу считают приближением искомой работы А силы 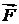 при перемещении материальной точки по кривой ВС:
при перемещении материальной точки по кривой ВС: 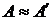 .
.
Пусть 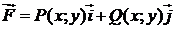 ,
,  ,
,
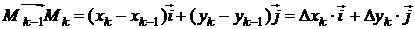 ,
,
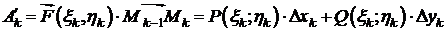 .
.
Тогда
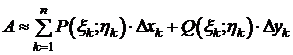 . (2)
. (2)
Пусть 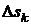 - длина
- длина 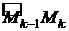 ,
,  . Переходя в (2) к
. Переходя в (2) к 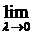 , получим точное равенство:
, получим точное равенство:
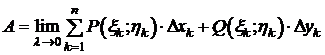 . (3)
. (3)
2. Определение криволинейного интеграла II типа
Пусть в плоскости  задана спрямляемая кривая
задана спрямляемая кривая 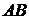 и вдоль нее определена функция f (x; y). Кривую
и вдоль нее определена функция f (x; y). Кривую 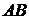 разобьем произвольно на
разобьем произвольно на  частей точками
частей точками 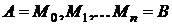 ,
, 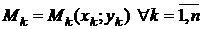 . На каждой частичной дуге
. На каждой частичной дуге 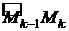 выберем произвольную точку
выберем произвольную точку 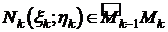 . Обозначим через D xk и D уk проекции дуги
. Обозначим через D xk и D уk проекции дуги 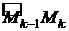 на оси координат, D xk = xk - xk -1, D yk = yk - yk -1. Разбиение обозначим через
на оси координат, D xk = xk - xk -1, D yk = yk - yk -1. Разбиение обозначим через 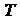 . Составим сумму
. Составим сумму
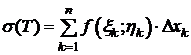 . (4)
. (4)
(4) – интегральная сумма для функции f (x; y) на кривой AB по координате x. Пусть  ,
, 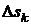 - длина частичной дуги
- длина частичной дуги 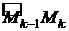 .
.
Определение 1. Число I называется пределом интегральной суммы 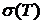 при
при 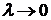 , если
, если  выполнено
выполнено 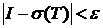 . Обозначается:
. Обозначается: 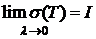 .
.
Определение 2. Если существует конечный предел интегральной суммы 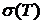 при
при 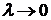 , не зависящий ни от способа разбиения кривой АВ, ни от выбора точек
, не зависящий ни от способа разбиения кривой АВ, ни от выбора точек 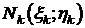 , то он называется криволинейным интегралом по координате х от функции f (x; y), взятым по кривой AB. Функция называется интегрируемой вдоль кривой AB по координате х,если для нее вдоль этой кривой существует криволинейный интеграл по x.
, то он называется криволинейным интегралом по координате х от функции f (x; y), взятым по кривой AB. Функция называется интегрируемой вдоль кривой AB по координате х,если для нее вдоль этой кривой существует криволинейный интеграл по x.
Обозначается: 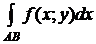 .
.
Таким образом,  .
.
Аналогично определяется криволинейный интеграл от функции f (x; y) по координате y, взятый по кривой AB:
 .
.
Криволинейные интегралы по координатам x и y называются криволинейными интегралами II типа.
Если вдоль кривой AB две функции P (x; y) и Q (x; y), и существуют 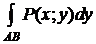 ,
, 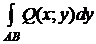 , то сумма этих интегралов также называется криволинейным интегралом II типа (общего вида) и обозначается:
, то сумма этих интегралов также называется криволинейным интегралом II типа (общего вида) и обозначается:
 .
.
Физический смысл криволинейного интеграла II типа
Из задачи о работе плоского силового поля и определения криволинейного интеграла II типа следует, что криволинейный интеграл II типа общего вида
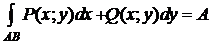 ,
,
то есть выражает работу силы  по перемещению материальной точки по кривой из точки А в точку В.
по перемещению материальной точки по кривой из точки А в точку В.
Замечание 1. Определенный интеграл является частным случаем криволинейного интеграла II типа. Пусть кривая АВ - это отрезок AB =[ a; b ] оси O x. Тогда f (x; y)= f (x;0)= F (x). Поэтому на [ a; b ]
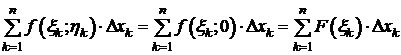 .
.
В правой части – обыкновенная интегральная сумма для функции F (x) на [ a; b ]. Переходя к 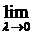 , получим
, получим
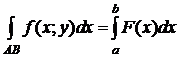 .
.
Аналогично, если кривая AB является некоторым отрезком [ c; d ] оси O y, то  , где F(y)= f (0; y), y Î[ c; d ].
, где F(y)= f (0; y), y Î[ c; d ].
Замечание 2. Если на кривой AB поменять направление интегрирования на противоположное, то и знак криволинейного интеграла II типа изменится на противоположный. Это происходит потому, что в интегральных суммах  изменяется знак
изменяется знак  . Таким образом, криволинейные интегралы II типа от одной и той же функции f (x; y), взятые по одной и той же кривой АВ, но в противоположных направлениях, равны по модулю, но противоположны по знаку:
. Таким образом, криволинейные интегралы II типа от одной и той же функции f (x; y), взятые по одной и той же кривой АВ, но в противоположных направлениях, равны по модулю, но противоположны по знаку:
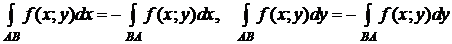 ,
,
 .
.
Следовательно, при вычислении криволинейных интегралов II типа необходимо учитывать направление интегрирования. Из двух направлений на кривой одно считают положительным, а другое – отрицательным.
 Если кривая замкнута и представляет собой контур, ограничивающий некоторую область на плоскости (это будет в случае, если замкнутая кривая не имеет кратных точек), то за положительное направление принимают обычно направление против хода часовой стрелки, а за отрицательное – по ходу часовой стрелки. Но для некоторых областей такой способ задания направления непригоден. В этом случае положительным направлением считают такое направление обхода контура, когда ограниченная им область (Р) остается все время слева. Интеграл по замкнутому контуру L обозначается:
Если кривая замкнута и представляет собой контур, ограничивающий некоторую область на плоскости (это будет в случае, если замкнутая кривая не имеет кратных точек), то за положительное направление принимают обычно направление против хода часовой стрелки, а за отрицательное – по ходу часовой стрелки. Но для некоторых областей такой способ задания направления непригоден. В этом случае положительным направлением считают такое направление обхода контура, когда ограниченная им область (Р) остается все время слева. Интеграл по замкнутому контуру L обозначается:  . Иногда с помощью стрелки указывают направление обхода:
. Иногда с помощью стрелки указывают направление обхода:
 или
или  .
.
3. Основные свойства криволинейного интеграла II типа
1º. Если функция f интегрируема вдоль кривой AB, 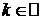 , то функция kf также интегрируема вдоль кривой AB, причем
, то функция kf также интегрируема вдоль кривой AB, причем
 .
.
2º. Если функции f и g интегрируемы вдоль кривой AB, то и функция f ± g интегрируема вдоль кривой AB, причем
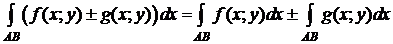 .
.
3º. (Аддитивность)
Для любой точки C кривой AB, если 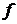 интегрируема вдоль кривой AB, то она интегрируема и вдоль кривых AС и СВ и
интегрируема вдоль кривой AB, то она интегрируема и вдоль кривых AС и СВ и
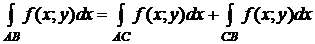 .
.
 4º. Если функция
4º. Если функция 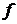 интегрируема вдоль кривой AB, то она интегрируема и вдоль кривой ВА, причем
интегрируема вдоль кривой AB, то она интегрируема и вдоль кривой ВА, причем
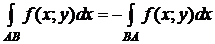 .
.
5º. Если 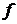 интегрируема по замкнутому контуру L, то величина криволинейного интеграла не зависит от того, какую точку контура принять за начальную:
интегрируема по замкнутому контуру L, то величина криволинейного интеграла не зависит от того, какую точку контура принять за начальную:  .
.
Действительно, из рисунка видно
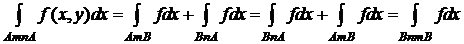 .
.
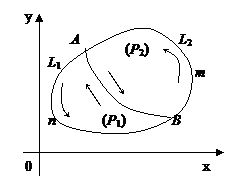 6º. Если область (P), ограниченную замкнутым контуром L разделить на две области (P 1) и (P 2), ограниченные контурами L 1 и L 2 соответственно, то интеграл в некотором направлении по кривой L равен сумме интегралов по контурам L 1 и L 2 в том же направлении:
6º. Если область (P), ограниченную замкнутым контуром L разделить на две области (P 1) и (P 2), ограниченные контурами L 1 и L 2 соответственно, то интеграл в некотором направлении по кривой L равен сумме интегралов по контурам L 1 и L 2 в том же направлении:
 .
.
Доказательство.
 .
.
4.Существование и вычисление криволинейных интегралов II типа
Теорема. Пусть кривая L=AB задана параметрическими уравнениями

где  и
и  - непрерывно дифференцируемые функции на [ a; b ]. При изменении параметра t от a до b кривая описывается от точки A к точке B. Пусть функции f (x; y), P (x; y), Q (x; y) непрерывны на кривой L (т. е. " M 0Î L
- непрерывно дифференцируемые функции на [ a; b ]. При изменении параметра t от a до b кривая описывается от точки A к точке B. Пусть функции f (x; y), P (x; y), Q (x; y) непрерывны на кривой L (т. е. " M 0Î L 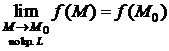 ). Тогда существуют
). Тогда существуют 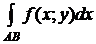 ,
, 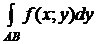 ,
, 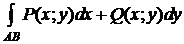 и справедливы соотношения:
и справедливы соотношения:
1)  ,
,
2)  ,
,
3) 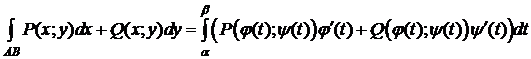 .
.
Доказательство.
 Докажем существование
Докажем существование 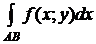 и равенство 1).
и равенство 1).
Возьмем произвольное разбиение 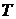 кривой
кривой 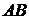 точками
точками 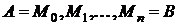 на n частичных дуг. Выберем произвольные точки
на n частичных дуг. Выберем произвольные точки 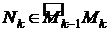
 и составим интегральную сумму
и составим интегральную сумму
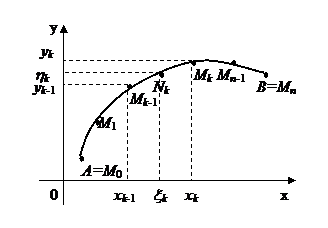
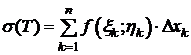 ,
,
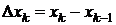 ,
,  .
.
Обозначим через tk значение параметра t, которому соответствует точка 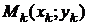 , а через tk - значение t, которому соответствует точка
, а через tk - значение t, которому соответствует точка 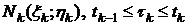 . Тогда
. Тогда

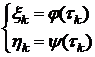 .
.
Подставим эти соотношения в 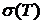 :
:
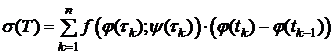 .
.
Согласно формуле Ньютона-Лейбница 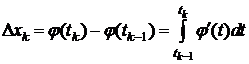 . Подставляя в последнее равенство, получим:
. Подставляя в последнее равенство, получим:
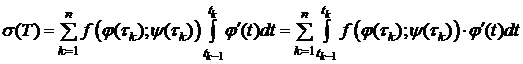 . (5)
. (5)
По условию f (x; y) непрерывна вдоль L, j (t), y (t), j ¢(t) непрерывны на [ a; b ], следовательно, функция f (j (t); y (t))× j ¢(t) интегрируема на [ a; b ].
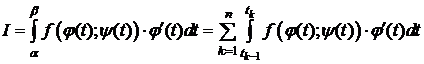 . (6)
. (6)
Рассмотрим разность  . Из (5), (6) следует
. Из (5), (6) следует
 .
.
Оценим модуль этой разности:
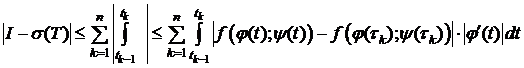 . (7)
. (7)
Так как  непрерывна на [ a; b ], то она ограничена на [ a; b ], то есть
непрерывна на [ a; b ], то она ограничена на [ a; b ], то есть 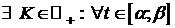 выполнено
выполнено 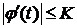 . (8)
. (8)
Так как 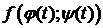 непрерывна на [ a; b ], то она равномерно непрерывна на [ a; b ], то есть
непрерывна на [ a; b ], то она равномерно непрерывна на [ a; b ], то есть 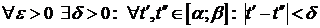 выполнено
выполнено
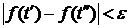 . (9)
. (9)
Если разбиение Т взять таким образом, что  , то есть
, то есть  , то
, то 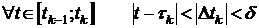
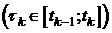 . Следовательно, для таких t выполнено (9):
. Следовательно, для таких t выполнено (9):
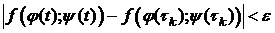 . (10)
. (10)
Тогда из (7), учитывая (8), (10), получим
 .
.
Таким образом, 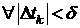 выполнено
выполнено
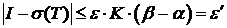 . (11)
. (11)
Обозначим 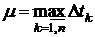 . Тогда из (11) следует, что
. Тогда из (11) следует, что
 . (12)
. (12)
Если 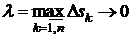 , то и
, то и 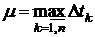 ®0. Тогда
®0. Тогда
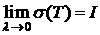 .
.
Þ 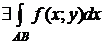 , и т.к.
, и т.к. 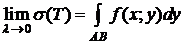 ,
, 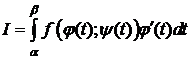 , то
, то
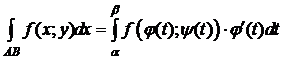 , то есть верно равенство 1).
, то есть верно равенство 1). 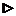
Замечание 1. Пусть кривая АВ задана явным уравнением y=j (x), где j определена и непрерывна вместе с 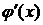 на [ a; b ], A = j (a), B = j (b). Пусть f непрерывна на кривой АВ. Тогда
на [ a; b ], A = j (a), B = j (b). Пусть f непрерывна на кривой АВ. Тогда
 ,
,  .
.
Аналогично, если кривая АB задана уравнением x = y (y), y Î[ c; d ], где y (y) непрерывно-дифференцируема на [ c; d ], то
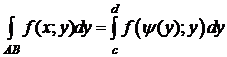 ,
, 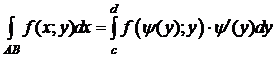 .
.
Замечание 2. Если кривая АВ представляет собой отрезок, параллельный оси O y, то  . Это следует из того, что в интегральной сумме
. Это следует из того, что в интегральной сумме 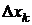 =0
=0  , следовательно,
, следовательно, 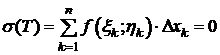 . Отсюда
. Отсюда  . Аналогично, если АВ – отрезок, параллельный оси O x, то
. Аналогично, если АВ – отрезок, параллельный оси O x, то 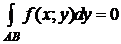 .
.
 Пример 1. Вычислить
Пример 1. Вычислить 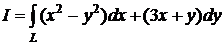 , если L - дуга параболы y=x 2 от точки (0;0) до точки (2;4).
, если L - дуга параболы y=x 2 от точки (0;0) до точки (2;4).
Δ I способ. y=x 2 Þ dy =2 xdx, x Î[0;2].
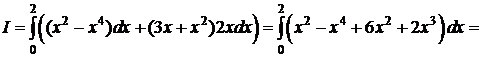
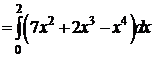
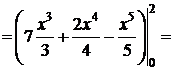
 .
.
II способ.  .
.

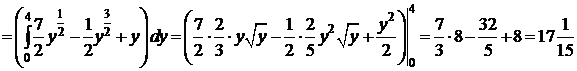 . D
. D
 Пример 2.
Пример 2. 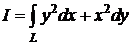 , где L - верхняя половина эллипса,
, где L - верхняя половина эллипса,  , проходимая по часовой стрелке.
, проходимая по часовой стрелке.
Δ 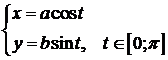 - параметрические уравнения кривой L (t изменяется от
- параметрические уравнения кривой L (t изменяется от 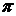 до 0!)
до 0!)
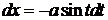 ,
,  .
.
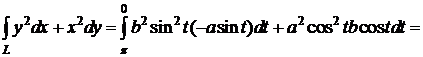
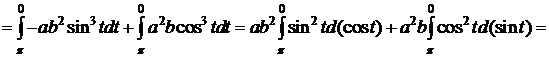
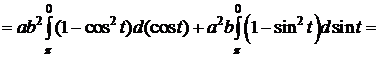
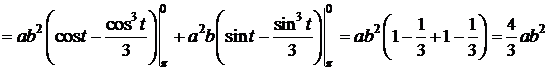 . Δ
. Δ
5. Формула Грина-Остроградского
Формула Грина-Остроградского связывает двойной интеграл по области (P) с криволинейным интегралом по границе (L) этой области.
I. Пусть область (P) ограничена контуром (L), состоящим из непрерывных кривых y=j 1(x), y=j 2(x), j 1(x)£ j 2(x) " x Î[ a; b ] и отрезков прямых x = a, x = b, a < b, то есть (P) - простая область I типа: (PI)
 Если функция P (x; y) вместе с
Если функция P (x; y) вместе с 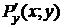 непрерывна на замкнутой простой области (PI), то справедлива формула
непрерывна на замкнутой простой области (PI), то справедлива формула
 , (1)
, (1)
где интегрирование по контуру берется в положительном направлении.
Доказательство.

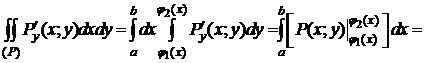
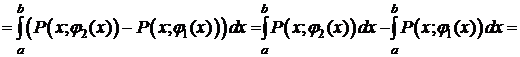
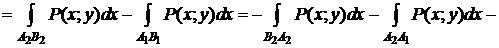
 .
. 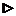
Формула(1) справедлива и для более сложных областей, которые можно разбить на конечное число областей I типа. Покажем это на следующем примере.
Пусть область 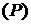 ограничена контуром (L).
ограничена контуром (L). 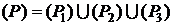 , где
, где  - простые области I типа. Обозначим
- простые области I типа. Обозначим  - контуры этих областей. Пусть
- контуры этих областей. Пусть 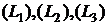 - части, на которые разбит контур (L).
- части, на которые разбит контур (L).
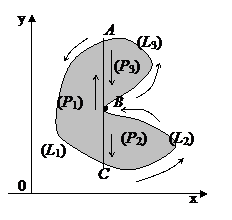
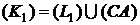 ,
, 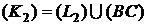 ,
,  .
.
К каждой из областей  применима формула (1).
применима формула (1).
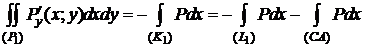 ,
,
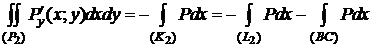 ,
, 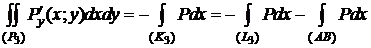 .
.
Сложив эти равенства, учитывая, что 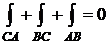 , получим формулу (1).
, получим формулу (1).
 II. Пусть область (P) ограничена кривой (L), состоящей из непрерывных кривых x = y 1(y), x = y 2(y), y 1(y)£ y 2(y) " y Î[ c; d ] и отрезками прямых y=c, y=d (c < d). То есть (P) - простая область II типа: (PII).
II. Пусть область (P) ограничена кривой (L), состоящей из непрерывных кривых x = y 1(y), x = y 2(y), y 1(y)£ y 2(y) " y Î[ c; d ] и отрезками прямых y=c, y=d (c < d). То есть (P) - простая область II типа: (PII).
Если функция 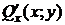 непрерывна на замкнутой области (PII), то справедлива формула
непрерывна на замкнутой области (PII), то справедлива формула
 . (2)
. (2)
Криволинейный интеграл в (2) берется в положительном направлении. Доказательство (2) аналогично доказательству формулы (1). Формула (2) справедлива и для более сложных областей, которые можно разбить на конечное число областей II типа.
III. Область (P) называется простой, если она одновременно является областью (PI) и (PII). Очевидно, любая прямая, параллельная осям координат, пересекает простую область не более, чем в двух точках.
Пусть (P) - простая область, (L) - ее контур. Тогда для этой области справедливы одновременно равенства (1) и (2). Вычитая (1) из (2) получим
 . (3)
. (3)
Из вышесказанного следует, что формула (3) справедлива и для области, которая может быть представлена в виде конечного числа простых областей. Итак, доказана следующая теорема.
Теорема. Пусть (P) - простая область (или область, представимая в виде конечного числа простых областей). Тогда если P (x; y) и Q (x; y) непрерывны вместе с частными производными  и
и 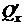 на замкнутой области (P), то справедлива формула (3).
на замкнутой области (P), то справедлива формула (3).
 Формула (3) называется формулой Грина – Остроградского. Ее можно доказать и для более общего случая: она справедлива и для области, которая ограничена одной или несколькими кусочно-гладкими кривыми.
Формула (3) называется формулой Грина – Остроградского. Ее можно доказать и для более общего случая: она справедлива и для области, которая ограничена одной или несколькими кусочно-гладкими кривыми.
Пример 1. С помощью формулы Грина – Остроградского вычислить криволинейный интеграл:
а) 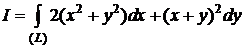 ,
,
б) 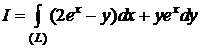 ,
,
где (L) - контур треугольника с вершинами A(1;1), B(2;2), C(1;3).
Δ а)  ,
,  ,
,
 ,
,  .
.
(AB): y=x, (BC): 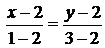 ,
, 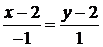 , x- 2=2 -y, y =4 -x.
, x- 2=2 -y, y =4 -x.
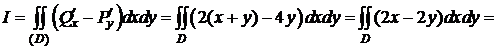


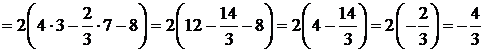 .
.
б) P (x; y)=2 ex-y, Q (x; y)= yex, 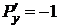 ,
, 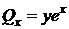 ,
,
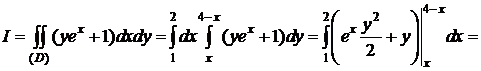
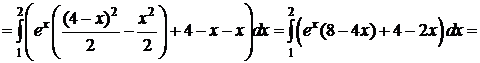


 . D
. D
Пример 2. С помощью формулы Грина вычислить интеграл
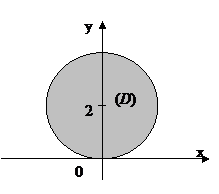
 ,
,  .
.
D (L): x 2+ y 2-4 y +4=4, x 2+(y- 2)2=4,
P (x; y)= ex sin y-y, 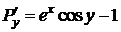 ,
,
Q (x; y)= ex cos y- 1, 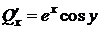 ,
,
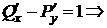
 .
.
Или  . D
. D
6. Вычисление площадей с помощью криволинейного интеграла
Пусть для области 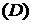 с границей (L) справедлива формула Грина (3):
с границей (L) справедлива формула Грина (3):
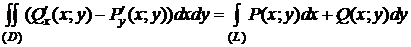 .
.
Полагая в (3) Q (x; y)= x, P (x; y)=0, получим
 . (4)
. (4)
Полагая в (3) Q (x; y)=0, P (x; y)= -y, получим
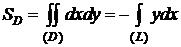 . (5)
. (5)
Складывая (4) и (5) и деля на 2, получим
 . (6)
. (6)
Для вычисления площади 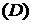 можно использовать любую из формул (4)-(6). Наиболее удобна последняя.
можно использовать любую из формул (4)-(6). Наиболее удобна последняя.
Пример 1. Вычислить с помощью криволинейного интеграла площадь фигуры, ограниченной кардиоидой
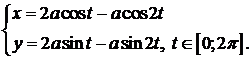
| t | 
| 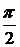
| 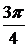
| 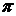
| 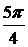
| 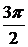
| 
| 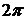
| |
| x | a | 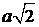
| a | - 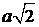
| -3 a | - 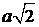
| a | 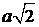
| a |
| y | 
| 2 a | 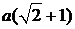
| 
| -2 a | 
|
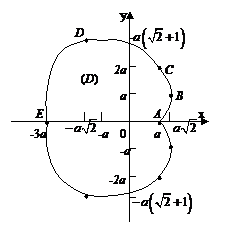
 ,
,
ABCDE: t Î[0; p ],
EA: y =0, dy =0 Þ 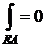 .
.
Следовательно,
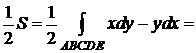
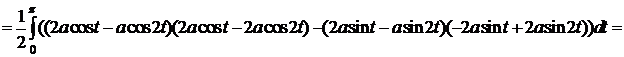
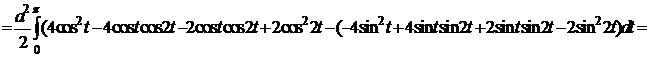
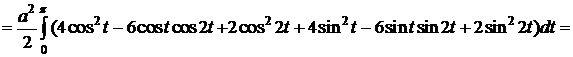
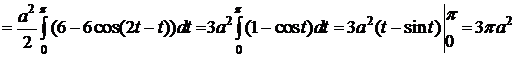 .
.
 .
.
7. Криволинейные интегралы, не зависящие от пути интегрирования
Вначале рассмотрим пример.
Пример.
 а) Вычислить
а) Вычислить  вдоль кривой: 1) y=x, 2) y=x 2, 3) y=x 3.
вдоль кривой: 1) y=x, 2) y=x 2, 3) y=x 3.
D 1)  ;
;
2) 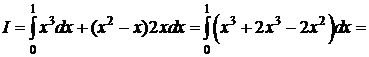
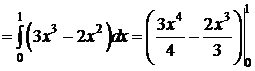
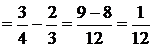 ;
;
3) 
 . D
. D
б) Вычислить 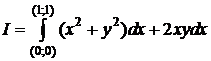 вдоль тех же кривых.
вдоль тех же кривых.
D 1)  ;
;
2) 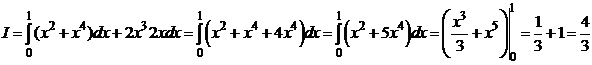 ;
;
3) 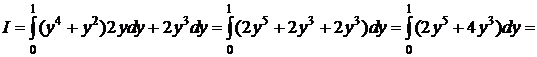
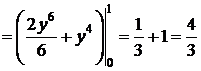 . D
. D
Можно доказать, что величина интеграла в примере б) зависит только от начала и конца пути интегрирования.
Далее будем все рассматриваемые кривые предполагать кусочно-гладкими.
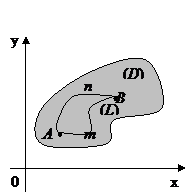
Определение. Область называется связной, если любые две точки области можно соединить ломаной, целиком лежащей в этой области.
Замкнутым контуром будем называть любую замкнутую кривую. Простой замкнутый контур – контур, не имеющий точек самопересечения. Например, на рисунке 3)- не простой замкнутый контур.
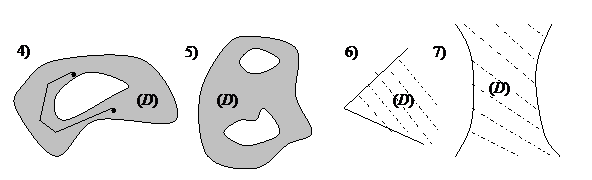
Определение. Связная область (D) называется односвязной, если любой замкнутый контур, лежащий в (D), ограничивает область, также целиком лежащую в (D) (рис. 1,6,7).
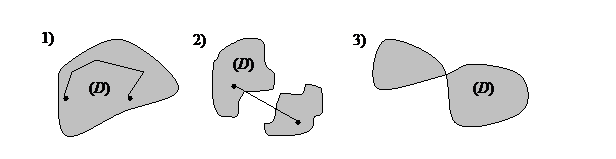
связная область несвязная область несвязная область
 |
связная область связная область связная связная
Иными словами, односвязная область не имеет дырок, даже точечных. Если область конечна, то определение односвязности можно сформулировать короче: область должна быть ограничена единственным замкнутым контуром. Если область неодносвязна, то ее называют многосвязной (рис. 4,5).
 Пусть на области (D) заданы две непрерывные функции P (x; y), Q (x; y). Возьмем любые две точки A, B Î(D) и зафиксируем их. Соединим точки А и В всевозможными кривыми (L)Ì(D). Тогда интеграл
Пусть на области (D) заданы две непрерывные функции P (x; y), Q (x; y). Возьмем любые две точки A, B Î(D) и зафиксируем их. Соединим точки А и В всевозможными кривыми (L)Ì(D). Тогда интеграл
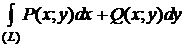 (1)
(1)
будет иметь различные значения в зависимости от 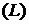 (пример а)).
(пример а)).
Определение. Если при любых фиксированных точках A, B Î(D) значение криволинейного интеграла (1) по любой кривой, лежащей в (D) и соединяющей точки А и В, одно и то же, то говорят, что (1) не зависит от пути интегрирования на области (D). В этом случае значение интеграла (1) определяется только заданием точек А и В.
Условия независимости криволинейного интеграла от пути интегрирования даются следующими теоремами.
 Теорема 1. Для того, чтобы криволинейный интеграл (1) не зависел от пути интегрирования на области (D) необходимо и достаточно, чтобы он был равен нулю на любом замкнутом контуре, лежащем в области (D).
Теорема 1. Для того, чтобы криволинейный интеграл (1) не зависел от пути интегрирования на области (D) необходимо и достаточно, чтобы он был равен нулю на любом замкнутом контуре, лежащем в области (D).
Доказательство.
 1)Необходимость.
1)Необходимость.
Пусть интеграл (1) не зависит от пути интегрирования. Докажем, что он равен нулю по любому замкнутому контуру (L)Ì(D). Выберем (L) = (AmB)  (BnA). Тогда
(BnA). Тогда
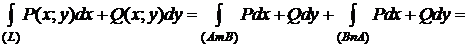
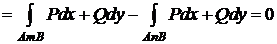 ,
,
так как (1) не зависит от пути интегрирования (то есть 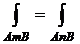 ).
).
2) Достаточность.
Пусть интеграл (1) по любому замкнутому контуру (L) равен 0. Докажем, что (1) не зависит от пути интегрирования в (D). Зафиксируем точки A и B и рассмотрим два пути, соединяющие их: (AnB) и (AmB). Эти два пути образуют замкнутый контур (AmB)  (AnB) = (L).
(AnB) = (L).
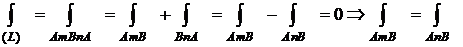 .
. 
Теорема 2. Пусть функции P (x; y) и Q (x; y) непрерывны вместе со своими частными производными  и
и 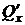 на области (D). Для того, чтобы криволинейный интеграл (1) на области (D) не зависел от пути интегрирования необходимо, а если (D) – односвязная, то и достаточно, чтобы во всех точках (D) выполнялось равенство
на области (D). Для того, чтобы криволинейный интеграл (1) на области (D) не зависел от пути интегрирования необходимо, а если (D) – односвязная, то и достаточно, чтобы во всех точках (D) выполнялось равенство
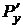 =
= 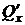 . (2)
. (2)
Доказательство.

 1) Необходимость.
1) Необходимость.
Пусть интеграл (1) на (D) не зависит от пути интегрирования. Докажем, что на (D) верно равенство (2). От противного. Пусть в некоторой точке (x 0; y 0): 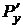 (x 0; y 0)
(x 0; y 0) 
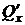 (x 0; y 0). Для определенности пусть
(x 0; y 0). Для определенности пусть 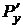 (x 0; y 0) <
(x 0; y 0) < 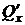 (x 0; y 0). Рассмотрим функцию F (x; y) =
(x 0; y 0). Рассмотрим функцию F (x; y) = 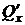 (x; y) -
(x; y) - 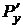 (x; y). F (x; y) непрерывна в точке (x 0; y 0)
(x; y). F (x; y) непрерывна в точке (x 0; y 0) 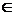 (D) и F (x 0; y 0) > 0. Тогда $ V (x 0; y 0): " (x; y)
(D) и F (x 0; y 0) > 0. Тогда $ V (x 0; y 0): " (x; y) 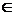 V выполнено F (x; y) > 0. Выберем произвольный простой замкнутой контур (L)
V выполнено F (x; y) > 0. Выберем произвольный простой замкнутой контур (L) 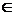 V. Применяя формулу Грина, получим:
V. Применяя формулу Грина, получим:
 . (3)
. (3)
Т.к. F (x; y) > 0, то по свойству двойного интеграла 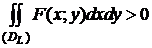 . Тогда из (3) следует
. Тогда из (3) следует 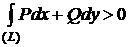 , что противоречит условию (по условию интеграл (1) не зависит от пути интегрирования в (D), следовательно, по теореме1
, что противоречит условию (по условию интеграл (1) не зависит от пути интегрирования в (D), следовательно, по теореме1 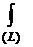 должен быть равен 0.)
должен быть равен 0.)
2) Достаточность.
Пусть на односвязной области (D) выполнено (2): 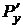 =
= 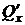 . Докажем, что интеграл (1) не зависит от пути интегрирования на (D). Пусть (L 1) – произвольный контур, лежащий в (D), (D 1) – область, ограниченная этим контуром. Т.к. (D) – односвязная область, то по определению (D 1)
. Докажем, что интеграл (1) не зависит от пути интегрирования на (D). Пусть (L 1) – произвольный контур, лежащий в (D), (D 1) – область, ограниченная этим контуром. Т.к. (D) – односвязная область, то по определению (D 1) 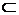 (D). По формуле Грина
(D). По формуле Грина
 .
.
По условию 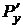 =
= 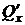 , тогда
, тогда  0
0 
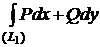 =0, следовательно (по теореме 1), интеграл (1) не зависит от пути интегрирования.
=0, следовательно (по теореме 1), интеграл (1) не зависит от пути интегрирования. 
Пример 1.  , где (L) – произвольный замкнутый контур, лежащий в
, где (L) – произвольный замкнутый контур, лежащий в 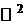 .
.
Δ P (x; y) = 2 xy, Q (x; y) =x 2.
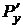 = 2 x,
= 2 x, 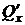 = 2 x,
= 2 x, 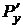 =
= 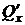 на
на 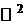 ,
, 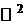 – односвязная область, следовательно, по теореме 2 данный интеграл не зависит от пути интегрирования в
– односвязная область, следовательно, по теореме 2 данный интеграл не зависит от пути интегрирования в 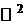 , следовательно, по теореме 1 он равен нулю по любому замкнутому контуру, лежащем в
, следовательно, по теореме 1 он равен нулю по любому замкнутому контуру, лежащем в 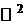 .
.
Ответ: I =0. Δ
Пример 2.  , (L): x 2 +y 2 =a 2 в положительном направлении.
, (L): x 2 +y 2 =a 2 в положительном направлении.
Δ  ,
, 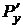 =
= 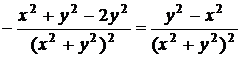 ,
,
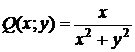 ,
,  =
= 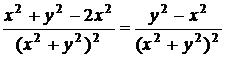 ,
,
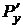 =
= 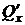 .
.
Параметрические уравнения окружности: 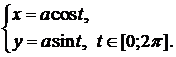
dx=-a sin tdt
Поделиться:
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-29
Нарушение авторских прав и Нарушение персональных данных