Потенциальная энергия упругой деформации (пружины)

Билет № 8

1)

Если у системы несколько осей симметрии, то центр масс лежит на их пересечении.

Уравнение изменения импульса механической системы.

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости: .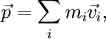

Закон сохранения импульса механической системы.

В замкнутой системе импульс сохраняется.

Другая формулировка: Суммарный импульс замкнутой системы остается постоянным по модулю и направлению, хотя импульс каждого из тел системы может изменяться.

Доказательство:

Рассмотрим механическую систему из N тел, массы и скорости которых соответсвенно равны m1, m2,..., mN; V1, V2,..., VN.

Запишем второй закон Ньютона для каждого из N тел механической системы:

где Fi - равнодействующая внутренних сил i-того тела системы, F - равнодействующая внешних сил i-того тела системы.

Проведем почленное сложение уравнений:

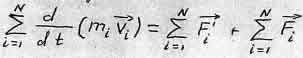(1)

Рассмотрим левую часть полученного выражения.

= =

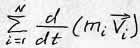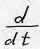
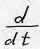
где = представляет собой суммарный импульс всех тел системы, т.е. импульс системы.

Первый член в правой части выражения (1) представляет собой векторную сумму внутренних сил всех тел системы. По третьему закону Ньютона каждой внутренней силе F'mn соответствует равная ей по модулю и противоположная по направлению сила F'nm, поэтому:

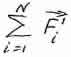=0.

Выражение 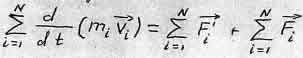преобразуется к виду:

=

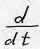
Производная от импульса системы по времени равна сумме внешних сил, действующих на систему.

Если сумма (векторная) внешних сил равна нулю, или внешние силы отсутствуют, то:

, т.е. импульс сохраняется.

 

2)Угловое ускорение: - физическая величина, характеризующая быстроту изменения угловой скорости твердого тела.

Угловое ускорение измеряется в рад/с²

 

Билет 9 Билет №9

1) Потенциальная энергия гравитационного притяжения:

Потенциальная энергия упругих деформаций:

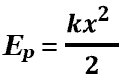
Или:

,

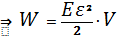где ;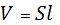

2) Импульсы механической системы – векторная физическая величина, являющаяся мерой механического движения тела.

 

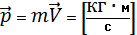
Билет 10

Билет № 10.

1) Момент инерции:

1. Стержня: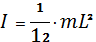

2. Обруча: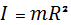

3. Диска: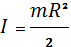

4. Шара (пустого):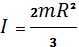

5. Шара (цельного):

Теорема Штейнера: 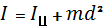, где d - расстояние от центра масс до оси вращения.

2) Момент импульса – вектором момента импульса относительно точки О называется 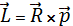, где 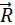– радиус-вектор из точки О.

 

 

Билет 11

Основной закон динамики (второй закон Ньютона) материальной точки имеет вид 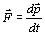, где 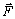– результирующая сила, действующая на материальную точку массы 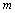, 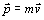– импульс материальной точки.

В случае основной закон динамики принимает вид .

 

 

 

 

 

 

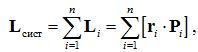2)моментом импульса механической системы (твердого тела) относительно неподвижной точки О называется вектор L _сист, равный геометрической сумме моментов импульса относительно той же точки всех материальных точек системы

где n – число материальных точек системы.

[L_сист] =кг·м/с

Билет 12

 

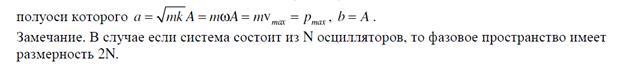
Билет 13

 

 

 

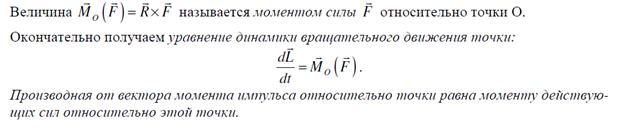
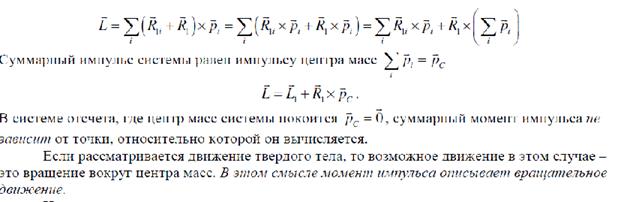
Билет 14

1) Вектор моменты силы – производная от момента импульса.

 

Вектором момента импульса относительно точки О называется вектор 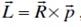, где R – радиус-вектор из точки О, p – вектор импульса точки.

Суммарный момент импульса системы относительно некоторой точки О: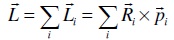

 

Производная от вектора суммарного момента импульса системы равно векторной сумме моментов сил, действующих на систему.

2) Вектор перемещения – «дельта»R за интервал времени(t1, t2) называется вектор, cоединяющий начальное (в момент времени t1) и конечное (в момент t2) положения точки.

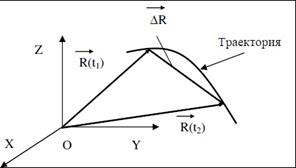
По определению, вектор перемещения равен векторной разности радиус-векторов:

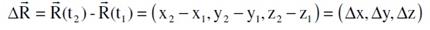
Величиной перемещения называют длина вектора R.

В СИ единицей измерения является метр (м).

 

Билет15

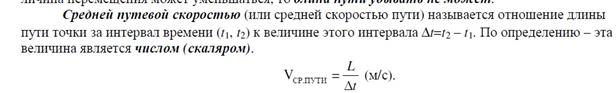
Ускоре́ние — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости 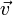точки (тела) при её (его) движении за единицу времени (ускорение учитывает не только изменение величины скорости, но и её направления):

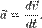
Нормальное ускорение отвечает за изменение скорости по направлению. Вектор нормального ускорения всегда направлен к центру кривизны траектории и перпендикулярно к тангенциальному ускорению.Нормальное ускорение также называют центростремительным

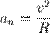
Тангенциальное успорение отвечает за изменение скорости по величине, вектор тангенциального ускорения всегда направлен по касательной к траектории в данной точке.

Величину тангенциального ускорения как проекцию вектора ускорения на касательную к траектории можно выразить так:

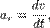
Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.

Моментом инерции твёрдого тела относительно плоскости называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояний от этой точки до плоскости. Единица измерения СИ: кг·м².

 

Билет 16

Консервативные силы.

Консервативной является сила, работа которой зависит только от начального и конечного положения тела в пространстве, но не зависит от пути, по которому двигается тело.

Работа таких сил на замкнутом пути равна 0. 1) сила всемирного тяготения 2) сила тяжести 3) сила кулоновского взаимодействия 4) сила упругости

Силы, действующие на частицу в центральном поле и в стационарном однородном, консервативны.

Поле консервативных сил является частным случаем потенциального силового поля.

Поле называется потенциальным, если его можно описать с помощью ф-ции П(x, y, z, t), градиент которой определяет силу в каждой точке поля.

Функция П называется потенциалом.

Когда потенциал не зависит явно от времени, то потенциальное поле оказывается стационарным.

t = 1/b - время релаксации затухающих колебаний (за t амплитуда уменьшается в e раз).

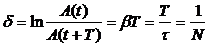- логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания.

 

Билет 17

В зависимости от характера воздействия на колеблющуюся систему различают свободные, вынужденные, автоколебания и параметрические колебания.

Гармонические колебания – колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса.

При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой () смещени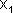й и 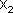, которые запишутся следующими выражениями:

, ,
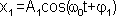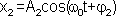Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:
= .
Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз (Рис. 1.2). 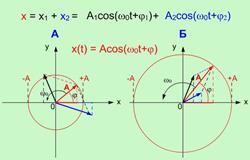На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм. Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний.
Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А 1 и А 2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А 1 и А 2 равен - π или π, то исходные колебания находятся в противофазе и суммарная амплитуда (А = 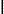А1 -А2 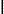) будет минимальна.

Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F

 

 

Билет 18

1.

Механическая энергия консервативной механической системы сохраняется во времени. При отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может никуда исчезнуть.

 

Для замкнутой системы физических тел, например, справедливо равенство

Ek1 + Ep1 = Ek2 + Ep2,

где Ek1, Ep1 — кинетическая и потенциальная энергии системы какого-либо взаимодействия,Ek2, Ep2 — соответствующие энергии после.

2.

Кинетическая энергия измеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки.

При вращательном движении роль массы m выполняет момент инерции I, а вместо линейной скорости v выступает угловая скорость ω, и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид: Tвр=Iω2/2

Билет 19

1. Амплитуда результирующего колебаний, получающегося при сложении двух гармонических колебаний одинакового направления и одинаковой частоты.

1) ₂ - 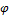₁ = ±2mπ (m = 0, 1, 2,...), тогда A=A₁+A₂, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;

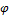2) ₂ - 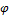₁ = ±(2m+1)π (m = 0, 1, 2,...), тогда A=|A₁–A₂|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.

Векторная диаграмма: гармоническое колебание представляется проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом 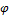, равным начальной фазе, и вращающегося с угловой скоростью W₀ вокруг этой точки.

 

Билет № 19

1. Сложение гармонических колебаний одного направления и равных частот. Векторная диаграмма.

 

Осциллятор – материальная точка или система, совершающая колебательное периодическое движение около положения устойчивого равновесия.

 

2. Объясните, что такое коэффициент трения скольжения. Укажите единицы измерения этой величины в СИ.

Коэффициент трения скольжения — отношение силы трения к нормальной составляющей внешних сил, действующих на поверхности тела.

Единицы измерения – не имеет.

 

 

Билет 20

1. Связь между потенциальной энергией и силой. Потенциальная энергия тяготения и упругих деформаций.

Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой точке потенциального поля соответствует некоторое значение силы F, действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой F и U должна быть связь, с другой стороны, dA = –dU, следовательно Fdr=-dU, отсюда:

Проекции вектора силы на оси координат: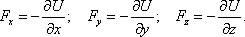

Вектор силы можно записать через проекции: , F = –grad U, где .

Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор направлен в сторону наибыстрейшего уменьшения U.

Потенциальная энергия упругой деформации (пружины)

Найдём работу, совершаемую при деформации упругой пружины.
Сила упругости Fупр = –kx, где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа dA = Fdx = –kxdx.
(Знак минус говорит о том, что работа совершена над пружиной). Тогда 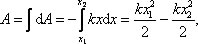, т.е. A = U1 – U2. Причем: U2 = 0, U = U1, тогда .

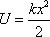На рис. 5.5 показана диаграмма потенциальной энергии пружины.

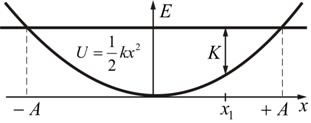
Рис. 5.5
Здесь E = K + U – полная механическая энергия системы, К – кинетическая энергия в точке x1.