Содержание
Введение ……………………………………………………………...………..4
1 Инструкция по работе с учебно-методическими указаниями …….……..5
2 Программа дисциплины ……………………………………………………5
3 Контрольная работа № 6 …………………………………………………...6
4 Задания на контрольную работу……….…………….…………….………9
5 Содержание и оформление контрольной работы ………………………..12
6 Вопросы для подготовки к зачету ………………………………………...12
7 Список рекомендуемой литературы……………………………………….13
Введение
Инженер в области математики должен иметь представление:
- о математике как особом способе познания мира, общности ее понятий и представлений;
- математическом моделировании;
- информации, методах ее хранения, разработки и передачи.
Знать и уметь использовать:
- основные понятия и методы математического анализа, аналитической геометрии, линейной алгебры, теории функций комплексного переменного, теории вероятностей и математической статистики, дискретной математики;
- математические модели простейших систем и процессов в естествознании и технике;
- вероятностные модели для конкретных процессов и проводить расчеты в рамках построенной модели.
Иметь опыт:
- употребления математической символики для выражения количественных и качественных отношений объектов;
- исследования моделей с учетом их иерархической структуры и оценки пределов применимости полученных результатов:
- использования основных приемов обработки экспериментальных данных;
- аналитического и численного решения алгебраических уравнений;
- исследования, аналитического и численного решения обыкновенных дифференциальных уравнений;
|
|
- аналитического и численного решения основных уравнений математической физики;
- программирования и использования возможностей вычислительной техники и программного обеспечения.
Цель курса «Математика»:
- дать студентам необходимую математическую подготовку для изучения общенаучных, общеинженерных и специальных дисциплин;
- привить студентам навыки логического и алгоритмического мышления;
- овладеть методами исследования и решения математических и прикладных задач по специальности;
- выработать умения самостоятельно расширять математические знания и применять их при анализе инженерных задач.
Инструкция по работе с учебно–методическим пособием
В разделе «Программа дисциплины» приведены темы и указывается, что необходимо знать в пределах каждой темы. В конце тем приводятся вопросы для самопроверки и литература из списка рекомендуемой литературы с указанием глав, страниц, где излагается материал темы.
Пример
Литература: [2, гл.2 с. 3-9], 4, с. 143-162],
Где 2 и 4 – порядковые номера литературных источников из списка рекомендуемой литературы.
Вариант контрольного задания выбирается по последней цифре шифра зачётной книжки. Последняя цифра шифра (0) соответствует 10 варианту в контрольном задании. В контрольной работе выполняются номера задач, оканчивающиеся на номер варианта. Например, последняя цифра 4, значит, выполняются задачи 4, 14, 24 и т.д.
Программа дисциплины
Тема 1. Уравнения математической физики.
Вопросы для самоконтроля
|
|
1. Классификация уравнений с частными производными второго порядка.
2. Уравнение теплопроводности.
3. Уравнение колебания струны.
Тема 2 .Элементы теории функций комплексного переменного.
Вопросы для самоконтроля
1. Производная и дифференциал функции комплексного переменного.
2. Аналитическая функция.
3. Необходимые и достаточные условия для аналитичности функции.
Тема 3. Операционное исчисление
Вопросы для самоконтроля
1. Определение преобразования Лапласа. Изображение и оригинал.
2. Свойства изображений и оригиналов.
3. Операционный метод решения дифференциальных уравнений с постоянными коэффициентами и их систем.
Тема 4. Теория вероятностей.
Вопросы для самоконтроля
1. Аксиомы теории вероятности и следствия из них.
2. Классическая вероятность.
3. Условная вероятность. Теоремы сложения и умножения вероятностей.
4. Формула полной вероятности и формула Байеса..
5. Локальная и интегральная теоремы Муавра-Лапласа.
6. Дискретные и непрерывные случайные величины. Их числовые характеристики.
Тема 5. Элементы математической статистики.
Вопросы для самоконтроля
1. Выборка, вычисление выборочной средней.
2. Точечные и интервальные оценки.
3. Доверительные интервалы.
Контрольные работы
Ниже приведены примеры выполнения расчетов.
К заданиям 1-10
Пример. Найти форму струны, определяемой уравнением 
, если 
Решение:
Имеем
т.е.
, или 
К заданиям 11-20
Пример: Представить заданную функцию w=f(z), где z=x+iy, в виде w =u(x,y)+iv(x,y); проверить, является ли она аналитической. Если да, то найти значение ее производной в заданной точке z0.
|
|
w=(iz)3, z0=-1+i
Решение:
Находим
Проверим условия Коши-Римана
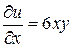
Условия Коши-Римана выполнены. Далее, имеем
К заданиям 21-31
Пример: Разложить функцию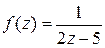 
в ряд Лорана в окрестности точки z0=0 и определить область сходимости этого ряда.
Решение:
Представим данную функцию в виде
В окрестности точки z0=0 выполняется неравенство 
, поэтому дробь 
можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом 
и знаменателем 
Отсюда получаем 
. Это разложение содержит только правильную часть. Из неравенства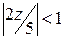 
заключаем, что область сходимости ряда является круг 
.
К заданиям 31-40
Пример: Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
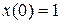
Решение: Перейдём к изображениям. Учитывая что:
и 
исходное уравнение примет вид:
т.е.
преобразуем правую часть и выразим x
Теперь разложим в сумму простых дробей, выражение стоящие в правой части применяя метод неопределённых коэффициентов:
Пусть 
тогда
В результате получим: 
т.е.
С учётом последнего равенства получаем
Ответ:
К заданиям 41-50
Пример:Решить систему уравнений
x(0)=0, y(0)=5
Решение: Переходя к изображениям, имеем
Решив эту систему относительно 
и 
, получаем
и 
.
Для определения воспользуемся второй теоремой разложения и формулой
.
имеем
Таким образом, 
Аналогично находим 
.
Задания на контрольную работу
Контрольная работа №1
Задачи 1-10
Задание 1. Методом Даламбера найти уравнение 
формы однородной бесконечной струны, определяемой волновым уравнением 
, если в начальный момент 
форма струны и скорость точки струны с абсциссой x определяются, соответственно, заданными функциями 
и 
1 
2 
3 
, 
4 
5 
6 
7 
8 
9 
1 0 
Задачи 11-20
Задание 2. Представить заданную функцию 
, где 
, в виде 
; проверить, является ли она аналитической. Если да, то найти значение ее производной в заданной точке 
.
11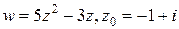 
16 
12 
17 
13 
18 
14 
19 
15 
20 
Задачи 21-30
Задание 3. Разложить функцию 
в ряд Лорана в окрестности точки 
и определить область сходимости этого ряда.
21 
26 
22 
27 
23 
28 
24 
29 
25 
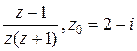30 
Задачи 31-40
Задание 4. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
31 
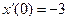
32 
33 
34 
35 
36 
37 
38 
39 
40 
Задачи 41-51
Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
41 
42 
43 
44 
45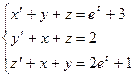 
46 
47 
48 
49 
50 
Содержание и оформление контрольных работ
5.1. Требования к оформлению контрольных работ: контрольные работы выполняются в тетради (12 л.). На обложке необходимо указать № к.р., свой факультет, специальность, шифр зачетной книжки, № варианта, ФИО, в случае электронного варианта работа выполняется в текстовом редакторе Word.
5.2. Требования к структуре контрольной работы: при выполнении работы необходимо приводить основные теоретические моменты, промежуточные математические доказательства, методики, формулы, расчеты.
В конце работы указывается список использованных источников, ставится число и личная подпись.
Вопросы для подготовки к экзамену (зачету)
1. Уравнения математической физики. Основные определения и понятия.
2. Классификация линейных дифференциальных уравнений второго порядка, канонические формы для уравнений с двумя переменными.
3. Начальные и граничные условия. Классификация задач по начальным и граничным условиям.
4. Уравнение колебаний. Задача Коши. Формула Даламбера.
5. Уравнение колебаний конечной струны. Метод Фурье.
6. Уравнение теплопроводности. Задача Коши. Формула Пуассона.
7. Уравнение теплопроводности для стержня конечной длины. Метод Фурье.
8. Основные определения и понятия функции комплексной переменной.
9. Предел, непрерывность функций комплексной переменной. Производная. Условия Коши-Римана.
10. Интегрирование функций комплексной переменной.
11. Аналитические функции. Теорема Коши. Интеграл Коши.
12. Ряды Тейлора и Лорана. Вычеты.
13. Оригинал и его изображение по Лапласу.
14. Свойства преобразования Лапласа.
15. Применение операционного исчисления для решения обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами.
16. Применение операционного исчисления для решения систем обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами.
17. Основные понятия теории вероятности.
18. Случайные события. Алгебра случайных событий.
19. Вероятность случайного события.
20. Основные соотношения между вероятностными событиями.
21. Классическая вероятностная схема.
22. Условные вероятности. Формула умножения вероятности.
23. Формула полной вероятности и формула Байесса.
24. Независимость случайных событий.
25. Формула Бернулли и формула Пуассона.
26. Случайные величины и их классификация. Функции распределения вероятностей.
27. Характеристики случайных величин..
28. Элементы математической статистики. Выборка и ее представление.
29. Оценка параметров распределения по выборке. Точечные и интервальные оценки.
30. Доверительный интервал и его нахождение.
Список рекомендуемой литературы
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для ВТУЗов. Т.2. ‑ М.: Интеграл-Пресс, 2004. – 544 с.
2. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 3: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2004. ‑ 511 с.
3. Мантуров О.В. Курс высшей математики: Ряды. Уравнения математической физики. Теория функций комплексной переменной. Численные методы. Теория вероятностей. - М.: Высш. шк., 1991. – 448 с.
4. Чистяков В.П. Курс теории вероятностей: Учеб. для втузов. ‑ М.: Агар, 1996. – 255 с.
5. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие. ‑ 11-е изд., стер. ‑ М.: Высш. школа, 2005. – 479 с.
6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие. ‑ 10-е изд., стер. ‑ М.: Высш. школа, 2005. – 404 с.
7. Фарлоу С. Уравнения с частными производными для научных работников и инженеров: Пер. с англ. - М.: Мир, 1985. – 384 с.
8. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.2: Учеб. пособие для втузов.-5-е изд., испр.- М.:Высшая школа, 1997. – 416 с.
9. Краснов М.А., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости: Учебное пособие, 2-е изд., перераб. и доп. - М.: Наука, Гл. редакция физико-математической литературы, 1981. – 304 с.
10. Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. - Спб.: «Лань», 1998. – 224 с.
11. Уравнения математической физики. Методическая разработка типовых расчетных заданий для студентов 3 курса энергетических специальностей дневной формы обучения /Кубан. гос. технолог. ун-т. Сост.: И.В. Терещенко, А.С. Трофимов, Н.И. Фомина. Краснодар, 2000, ‑ 23с.
12. Математическая физика. К выводу некоторых уравнений математической физики. Методические указания для студентов 2 курса заочной формы обучения специальностей 0906, 1007, 1004 /Кубан. гос. технолог. ун-т. Сост.: И.В. Терещенко, А.С. Трофимов, Н.И. Фомина. Краснодар, 2000. – 35 с.
13. Математическая физика. Решение задач, приводящих к уравнению теплопроводности и уравнению Лапласа. Методические указания для студентов 2 курса заочной формы обучения специальностей 0906, 1007, 1004. /Кубан. гос. технолог. ун-т. Сост.: И.В. Терещенко, А.С. Трофимов, Н.И. Фомина. Краснодар, 2000. 23 с.