Опорные величины для оценки риска

Оценка и учет риска при принятии решений

Задание.

Для определенной Вами в лабораторной работе №2 матрицы решений выбрать определенные вариантом задания опорные величины для оценки риска и для каждого варианта решения рассчитать возможный и относительный дефект выбора этого варианта решения, определить оптимальный выбор с точки зрения минимального дефекта и с точки зрения, допускающей определенный риск e_доп.

Теоретическая часть

Полное устранение риска при принятии решений зачастую не требуется. Определенная степень риска даже вводится сознательно, так как принятие решения без риска может оказаться невыгодным. Но любой риск при этом должен учитываться по возможности полно (описываться количественно и ограничиваться) и не превышать уровня, при котором результат достигается с достаточной надежностью.

Принятие решения при наличии риска

При оценке риска выбирают опорное для оценки значение Z (например, оптимум по минимаксному критерию Z_MM). Это опорное значение используется для определения степени неоптимальности варианта решения E_i в виде так называемого дефекта варианта решения E_i относительно опорного значения оценочной функции: .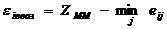

Максимальную разность дефектов при рассмотрении всех возможных вариантов решения E_i, i=1, ..., m, характеризуют как возможный риск:

.

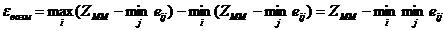Возможный риск независимо от информации о параметрах, имеющейся по результатам выборки, а также от числа реализаций процесса принятия решения представляет собой максимально возможную величину нереализуемой полезности решения.

В некоторых случаях имеет смысл выйти за рамки строгого следования минимаксному критерию, если принимающий решение готов пойти на некоторый риск, определяемый величиной . Для некоторых внешних условий, имеющих большую вероятность реализации, могут получиться варианты решения, которые дают заметный выигрыш по сравнению с оптимальным опорным значением варианта решения (например, оптимальным решением по ММ-критерию). С целью оценки конкурентоспособности таких решений для каждого варианта E_i вводят специальную величину, равную сумме минимального результата , j = 1, ..., n, и эффекта риска: 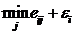, где .

Максимальный риск при рассмотрении всех вариантов решения E_i, i = 1, ..., m, равен . Оценочная функция при этом принимает вид: , где V(a)_i - один из доверительных факторов, h_j - частота (или, если известна, вероятность) возникновения внешнего условия F_j.

Множество всех вариантов решения, обеспечивающих максимум величины m_i :

.

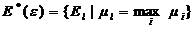Опорные величины для оценки риска

Риском считают реализацию случая, когда вариант решения E_i при внешнем условии F_j дает результат меньше ожидаемого. Такую ожидаемую величину и принимают в качестве опорной для оценки риска. Опорные величины разделяют на зависящие и не зависящие от внешних факторов.

Не зависящей от внешних факторов опорной величиной e_z может быть любая вещественная величина из диапазона .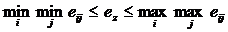

Величина 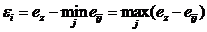называется возможным дефектом выбора варианта решения E_i. Так как отрицательные значения e_i не могут считаться дефектом, то будем рассматривать величину в качестве характеристики варианта решения E_i. Вариант решения E_i будет иметь дефект, когда , и будет свободен от дефекта, когда .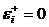

В качестве значений для независящих от внешних факторов опорных величин оценки риска используют значения известных критериев принятия решения (например, минимаксного критерия).

Опорную величину e_z, зависящую от внешних факторов, представляют в виде функции от всех m×n значений результатов решения e_ij: , где i = 1, ..., m, j = 1, ..., n. Тогда дефект, возможный при выборе варианта решения E_i, определяется как .

Выбор оптимального варианта дает минимальный дефект .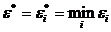

Относительный риск при выборе соответствующего варианта решения E_i определяется как разность между дефектом e_i варианта решения E_i и минимальным дефектом e^* : .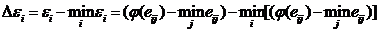

Опорные величины могут быть определены для каждого из n внешних состояний F₁, ..., F_n отдельно с помощью функции m переменных: , имеющей смысл в диапазоне .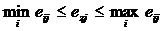

Возможным дефектом выбранного варианта решения E_i или оценкой риска, сопутствующего такому решению, называется величина 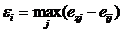, у которой учитываются только положительные значения .

В качестве зависимых от внешних факторов опорных величин выбираются, например, граничные значения диапазона определения опорной величины:

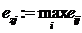и , а также среднее значение .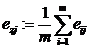

Оптимальный выбор варианта решения дает минимальный дефект .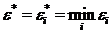

Относительный риск выбора варианта решения E_i:

.

Варианты задания

В столбце 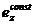задан критерий выбора, определяющий опорную величину, не зависящую от внешних факторов;

В столбце 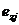- определяется способ вычисления опорной величины, зависящей от внешних факторов, следующим образом:

max - означает вычисление по формуле ,

min - по формуле ,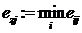

среднее - ;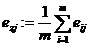

В столбце e_доп задан уровень допустимого риска в процентах от максимально возможного.

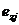
Номер варианта	Вид доверительного фактора	a			eдоп %
	эмпирический	0,05	MM	min
	прогностический	0,05	S	max
	эмпирический	0,1	BL	среднее
	прогностический	0,1	G	min
	эмпирический	0,2	HL	max
	прогностический	0,2	HW	среднее
	эмпирический	0,3	BL(MM)	min
	прогностический	0,3	P	max
	эмпирический	0,001	MM	среднее
	прогностический	0,001	S	min
	эмпирический	0,005	BL	max
	прогностический	0,005	G	среднее
	эмпирический	0,01	HL	min
	прогностический	0,01	HW	max
	эмпирический	0,02	BL(MM)	среднее
	прогностический	0,02	P	min
	эмпирический	0,025	MM	max
	прогностический	0,025	S	среднее
	эмпирический	0,03	BL	min
	прогностический	0,03	G	max