Первый алгоритм метода
Пусть требуется решить систему линейных алгебраических уравнений
 (1)
(1)
с положительно определенной матрицей A порядка n.
Рассмотрим функционал
 , (2)
, (2)
представляющий многочлен второго порядка относительно x1, x2, …, xn. Обозначим через 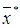 решение системы (1), т.е.
решение системы (1), т.е.  . В силу симметричности и положительной определенности матрицы, имеем:
. В силу симметричности и положительной определенности матрицы, имеем:

При этом знак равенства возможен лишь при  . Таким образом, задача решения уравнения (1) сводится к задаче отыскания вектора
. Таким образом, задача решения уравнения (1) сводится к задаче отыскания вектора  , обращающего в минимум функционал (2).
, обращающего в минимум функционал (2).
Для отыскания такого вектора применим следующий метод.
Пусть  – произвольный начальный вектор, а
– произвольный начальный вектор, а
 (4)
(4)
– вектор невязок системы. Покажем, что вектор невязок  имеет направление нормали к поверхности
имеет направление нормали к поверхности  в точке
в точке  . В самом деле, направление нормали совпадает с направлением быстрейшего изменения функции
. В самом деле, направление нормали совпадает с направлением быстрейшего изменения функции  в точке
в точке  . Это направление мы найдем, если найдем среди векторов
. Это направление мы найдем, если найдем среди векторов  , для которых
, для которых  , такой вектор, что
, такой вектор, что

имеет наибольшее значение. Но

Но среди векторов  постоянный длины
постоянный длины  достигает максимального значения, если
достигает максимального значения, если  имеет направление вектора
имеет направление вектора  или ему противоположное. Утверждение доказано. Будем двигаться из точки
или ему противоположное. Утверждение доказано. Будем двигаться из точки  в направлении вектора
в направлении вектора  до тех пор, пока функция
до тех пор, пока функция  достигает минимального значения. Это будет при
достигает минимального значения. Это будет при  , т.е. при
, т.е. при
 . (5)
. (5)
Вектор
 (6)
(6)
и принимаем за новое приближение к решению.
В методе сопряженных градиентов следующее приближение  находится так. Через точку
находится так. Через точку  проведем гиперплоскость (n-1) – го измерения
проведем гиперплоскость (n-1) – го измерения
 (7)
(7)
и через 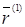 обозначим новую невязку системы
обозначим новую невязку системы
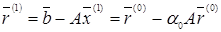 . (8)
. (8)
Вектор 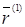 направлен по нормали к поверхности
направлен по нормали к поверхности  в точке
в точке  , а вектор
, а вектор 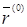 параллелен касательной плоскости в этой точке. Поэтому
параллелен касательной плоскости в этой точке. Поэтому
 . (9)
. (9)
Гиперплоскость (7) проходит через точку  , так как
, так как
 .
.
При любом  вектор
вектор  параллелен некоторой нормальной плоскости к поверхности
параллелен некоторой нормальной плоскости к поверхности  в точке
в точке  . Найдем среди них тот, который лежит в гиперплоскости (7), т.е. ортогонален к
. Найдем среди них тот, который лежит в гиперплоскости (7), т.е. ортогонален к  . Из условия ортогональности имеем:
. Из условия ортогональности имеем:
 ,
,
или
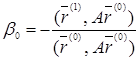 . (10)
. (10)
Вектор
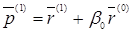 (11)
(11)
имеет направление нормали к сечению поверхности  гиперплоскости (7) в точке
гиперплоскости (7) в точке  . Будем двигаться из точки
. Будем двигаться из точки  в направлении вектора
в направлении вектора  до тех пор, пока функция
до тех пор, пока функция  достигнет минимума. Это будет при
достигнет минимума. Это будет при
 . (12)
. (12)
Вектор

примем за новое приближение к решению 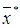 системы. Вектор невязок
системы. Вектор невязок
 (13)
(13)
имеет направление нормали к поверхности  в точке
в точке  . Покажем, что он будет ортогонален к
. Покажем, что он будет ортогонален к 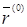 и
и  . В самом деле, используя (9), (11), (12), (13), имеем:
. В самом деле, используя (9), (11), (12), (13), имеем:

Рассмотрим гиперплоскость (n-2) – х измерений
 , (14)
, (14)
проходящую через точку  . Эта гиперплоскость содержит и
. Эта гиперплоскость содержит и  , так как мы ранее видели, что
, так как мы ранее видели, что  , а
, а
 .
.
Вектор  при любом
при любом  параллелен гиперплоскости (7), так как
параллелен гиперплоскости (7), так как
 .
.
Подберем  так, чтобы он был параллелен и гиперплоскости (14), т.е. потребуем ортогональности к вектору
так, чтобы он был параллелен и гиперплоскости (14), т.е. потребуем ортогональности к вектору  . Будем иметь:
. Будем иметь:
 ,
,
или
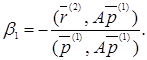 (15)
(15)
Вектор
 (16)
(16)
будет иметь направление нормали к сечению поверхности  гиперплоскостью (14) в точке
гиперплоскостью (14) в точке  . Из точки
. Из точки  сместимся в направлении этого вектора так, чтобы функция
сместимся в направлении этого вектора так, чтобы функция  достигла минимального значения. Это будет при
достигла минимального значения. Это будет при
 , (17)
, (17)
 (18)
(18)
примем за новое приближение к  . Новый вектор невязок будет:
. Новый вектор невязок будет:
 . (19)
. (19)
Продолжая процесс, получим последовательности векторов  ,
,  ,
,  , определяемые рекуррентными соотношениями:
, определяемые рекуррентными соотношениями:
 (20)
(20)
Для этих векторов имеют место следующие соотношения:
 (21)
(21)
 (22)
(22)
В самом деле, в силу самого построения при i¹j

Далее, при i>j

Если i=j+1, то правая часть равна нулю, в силу определения  , если же i>j+1, то
, если же i>j+1, то  , по доказанному, и
, по доказанному, и
 .
.
Продолжая понижение индекса у вектора  , через несколько шагов придем к скалярному произведению
, через несколько шагов придем к скалярному произведению  (по определению
(по определению  ). Таким образом, соотношения (21) доказаны. Для доказательства (22), в силу равноправия индексов i и j, предположим, что i>j. Тогда
). Таким образом, соотношения (21) доказаны. Для доказательства (22), в силу равноправия индексов i и j, предположим, что i>j. Тогда
 .
.
Так как в n-мерном векторном пространства не может быть более n взаимно ортогональных векторов, то на некотором шаге  получим
получим 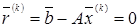 , т.е.
, т.е.  будет решением системы (1).
будет решением системы (1).
На рис. 1 показана геометрическая картина нашего построения при n=3.

Рис. 1
Второй алгоритм метода
Приведем другой алгоритм метода. Будем обозначать последовательные приближения к решению через  и введем обозначения:
и введем обозначения:
 . (23)
. (23)
Первые два приближения  и
и  возьмем так, чтобы
возьмем так, чтобы
 . (24)
. (24)
Предположим, что уже известно приближение  (i³1), вычислены
(i³1), вычислены  и справедливо равенство
и справедливо равенство
 . (25)
. (25)
Будем искать минимум функционала (2) на множестве векторов
 . (26)
. (26)
Приравнивая к нулю частные производные от  по
по  и
и  для определения
для определения  и
и  , получим систему:
, получим систему:
 (27)
(27)
или, учитывая (25),
 (28)
(28)
Обозначим через  решение этой системы:
решение этой системы:
 (29)
(29)
и за (i+1) – е приближение к решению примем:
 (30)
(30)
Из системы (27) следует, что
 , (31)
, (31)
а так как

то из (31) следует:
 (32)
(32)
Докажем, что если
 (33)
(33)
то при всех i
 (34)
(34)
что будет доказывать и сходимость, и конечность второго алгоритма.
В самом деле, при условиях (33)

и

т.е. условие (24) выполнено. Предположим, что уже доказаны равенства
 (35)
(35)
и докажем равенство

При предположении (35)  и, следовательно,
и, следовательно,

Но из соотношений (20) имеем:

т.е.

Докажем коллинеарность векторов
 и
и  (36)
(36)
Из (20) и (29) имеем:

а это и доказывает коллинеарность векторов (36).
Вектор  дает минимум функционала в плоскости, проходящей через
дает минимум функционала в плоскости, проходящей через  и натянутой на векторы
и натянутой на векторы  и
и  , а мы показали, что этот минимум лежит на прямой, проходящей через
, а мы показали, что этот минимум лежит на прямой, проходящей через  в направлении вектора
в направлении вектора  . Но на этой прямой минимум функционала достигается на векторе
. Но на этой прямой минимум функционала достигается на векторе  . Это и означает, что
. Это и означает, что 
Это и доказывает справедливость (34) при всех i.
На первый взгляд кажется, что первый алгоритм лучше, так как на каждом шаге он требует лишь одного умножения матрицы А на вектор  , а во втором алгоритме требуется два умножения матрицы А на вектор
, а во втором алгоритме требуется два умножения матрицы А на вектор  и
и  , но опыт показал, что применение первого алгоритма приводит к быстрому накоплению ошибок округления, так что для матриц большого порядка возможно существенное отклонение от точного решения. Второй алгоритм менее чувствителен к ошибкам округления и поэтому требует меньшего количество шагов для получения хорошего приближенного решения.
, но опыт показал, что применение первого алгоритма приводит к быстрому накоплению ошибок округления, так что для матриц большого порядка возможно существенное отклонение от точного решения. Второй алгоритм менее чувствителен к ошибкам округления и поэтому требует меньшего количество шагов для получения хорошего приближенного решения.
Метод сопряженных градиентов целесообразно использовать для решения систем уравнений, в которых матрица А имеет много нулевых элементов. При решении системы по этому методу элементы матрицы участвуют в арифметических операциях лишь при умножении матрицы на вектор, а умножение матрицы на вектор можно организовать так, чтобы в арифметических операциях участвовали только ненулевые элементы.
Заключение
В данной работе были рассмотрены метод ортогонализации и метод сопряженных градиентов, а также представлена программа на языке программирования С++, реализующая метод ортогонализации на ЭВМ, и ее результаты работы.
Список литературы
1. Березин И.С. и Жидков Н.П. Методы вычислений. т. 1. М.: «Наука», 1965. 633c.
2. Воеводин В.В. Численные методы алгебры (теория и алгоритмы). М.: «Наука», 1966.
3. Подбельский В.В. и Фомин С.С. Программирование на языке Си. М.: «Финансы и статистика», 2000. 599 с.
4. Калиткин Н.Н. Численные методы. М.: «Наука», 1978. 512 с.