Задания для самостоятельного решения. 1. Вычислить интеграл .

1. Вычислить интеграл .

Ответ. .

2. Расставить пределы интегрирования в двойном интеграле, если задана область интегрирования D:

а) D: ;

б) D: ;

в) D: .

Ответ. а) = ;

б)

;

в) = .

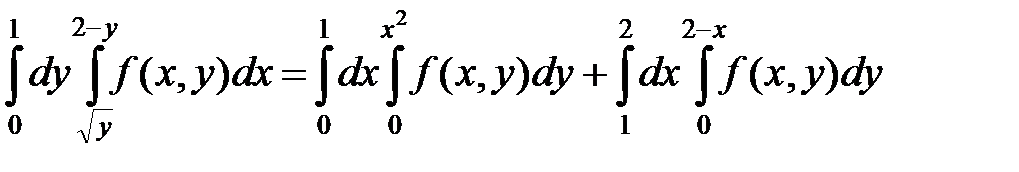3. Изменить порядок интегрирования в повторных интегралах:

а) ;

б) .

Ответ. а) ; б) .

4. Вычислить двойные интегралы:

 

а) , если D: , , ;

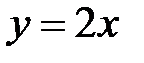б) , если D: , , .

Ответ. а) 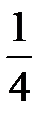; б) .

 

7.2. Вычисление тройного интеграла
в декартовых координатах

Область будем называть правильной в направлении оси Oz, если:

1) любая прямая, параллельная оси Oz и проходящая через внутреннюю точку области V, пересекает ее границу ровно в двух точках;

2) проекцией области V на плоскость Oxy является правильная область S (рис. 7.12).

x

y

z

0

1

2

S

V

Рис. 7.12. Правильная область в направлении оси Oz

Аналогично определяется область, правильная в направлении осей Ox и Oy.

При вычислении тройного интеграла

будем считать, что область V правильная в направлении оси Oz, а . «Снизу» область V ограничивает поверхность , а «сверху» – . Проекцию S области V на плоскость Oxy в направлении оси Oy ограничивают кривые и (рис. 7.13).

В декартовых прямоугольных координатах элемент объёма записывается в виде

Получим формулу для вычисления тройного интеграла в декартовых координатах:

= .

 

 

x

y

z

0

S

a

b

1

2

 

Рис. 7.13. Вычисление тройного интеграла

 

Итак,

(7.4)

Интеграл, стоящий в правой части формулы (7.4), называется трехкратным интегралом.

Интегрирование по области V, правильной в направлении оси Ox или Oy, выполняется аналогично.

Сформулируйте самостоятельно правило вычисления тройного интеграла.

 

Пример 1. Вычислить интеграл .

Решение

=

.

z

x

y

0

1

2

2

Рис. 7.14. Область, ограниченная конусом и плоскостями

Пример 2. Вычислить тройной интеграл

,

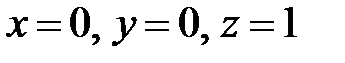
где V – область, расположенная в первом октанте, ограниченная конусом и плоскостями 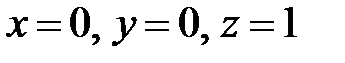(рис. 7.14).

Решение

Используя (7.4), имеем

=

=

 

z

х

у

у = 1 - х

z = 1 - х- y

Рис. 7.15. Область, ограниченная плоскостями

Пример 3. Вычислить

,

если V − область, ограниченная плоскостями .

Решение

Построим область, ограниченную плоскостями (рис. 7.15).

 

 

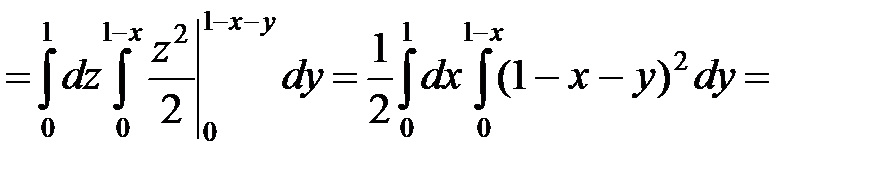
Задания для самостоятельного решения

1. Подумайте, при каком условии все пределы интегрирования в (7.4) будут постоянными величинами.

2. Запишите формулу вычисления тройного интеграла в случае области V, правильной в направлении оси Oy.

3. Вычислите интеграл . Ответ. .

4. Вычислите тройной интеграл , если V – область, ограниченная поверхностями . Ответ. .

7.3. Замена переменных в кратных интегралах

7.3.1. Общая формула замены переменных

Рассмотрим в Е³ три семейства поверхностей

(7.5)

Поверхности называют координатными поверхностями, а линии их пересечения – координатными линиями.

Тогда все точки пространства можно задать тройкой чисел − криволинейными координатами точки. А соотношение (7.5) можно считать формулами преобразования координат. Элемент объёма в этой системе координат тоже криволинейный, и уже нельзя считать, что он равен произведению трех измерений

Если соотношения (7.5) разрешить относительно x, y, z

то получим отображение области V пространства Oxyz на область V₁ пространства (рис. 7.16). При этом взаимная однозначность отображений гарантируется условием

. (7.6)

z

x

y

 

Рис. 7.16. Преобразование координат (x, y, z) в ()

 

Определитель в (7.6) называется функциональным определителем или Якобианом6 [1]. Можно показать, что коэффициент искажения элементарного объёма равен модулю Якобиана, т. е.

Отсюда для тройного интеграла имеем

Для двойного интеграла формулы будут выглядеть проще:

1) формулы преобразования

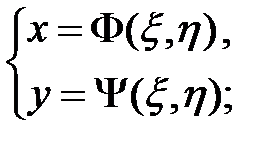
2) Якобиан

;

3) формула замены переменных в двойном интеграле

.

7.3.2. Вычисление двойного интеграла в полярных координатах

Положение точки М на плоскости можно определить, задав величины:

1) расстояние r от этой точки до начала координат 0;

2) угол между радиусом-вектором и осью Ox (рис. 7.17).

у

r

М (х,у) М (r,θ)

х

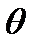
Рис. 7.17. Задание точки на плоскости

При этом считают, что .

Упорядоченная пара чисел (r, называется полярными координатами точки М. Связь с декартовыми координатами осуществляется при помощи формул

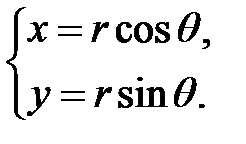
Якобиан

.

Тогда двойной интеграл в полярных координатах

.

Пример 1. Вычислить

Решение

Воспользуемся формулами перехода от декартовых координат к полярным

Так как , то область D – это верхний полукруг радиуса , т. е. изменяется от 0 до . Тогда

 

Пример 2. Переходя к полярным координатам, вычислить двойной интеграл

y

x

2a aa

Рис. 7.18. Окружность с центром в точке (a; 0) радиуса a

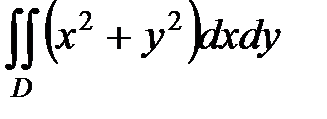, где D – окружность .

Решение

Преобразуем уравнение окружности

.

Это окружность с центром в точке (a; 0) радиуса a (рис. 7.18). Запишем уравнение окружности в полярных координатах

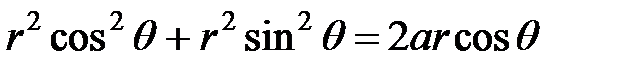, т.е. .

Причем изменяется в пределах от до , а r – от 0 до . Тогда

=

.

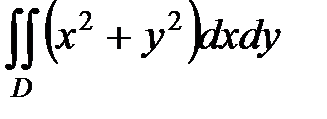Пример 3. Перейти в двойном интеграле к полярным координатам и расставить пределы интегрирования, если

.

=3

r= 1

Рис. 7.19. Область, ограниченная линиями

Решение

Область D изображена на рис. 7.19. Перейдем к полярным координатам

.

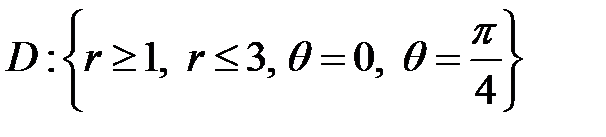Тогда

.

 

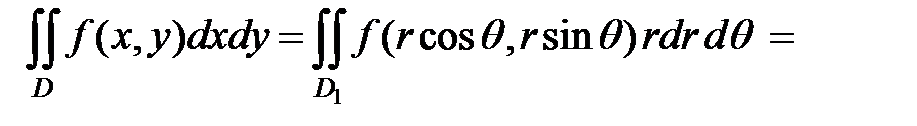
Пример 4. Вычислить интеграл

Решение

Для решения перейдем к обобщённым полярным координатам

При этом область S преобразуется в область , коэффициент искажения элемента площади будет равен , где

Поэтому

7.3.3. Вычисление тройного интеграла
в цилиндрических координатах

Положение любой точки М в пространстве можно определить, задав три величины:

1) расстояние r от этой точки до оси Oz;

2) угол θ между координатной плоскостью Oxz и плоскостью, проходящей через точку М и ось Oz;

3) расстояние z от точки М до координатной плоскости Oxy (рис. 7.20).

4) При этом предполагается, что

x

z

y

0

z

r

Рис. 7.20. Задание цилиндрических координат

Упорядоченная тройка чисел ( называется цилиндрическими координатами точки М, которые связаны с декартовыми координатами соотношениями:

Цилиндрическая система координат является ортогональной (ортогональны касательные плоскости к координатным поверхностям Координатными поверхностями здесь являются поверхности:

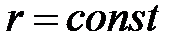· – цилиндрическая поверхность;

· – плоскости, проходящие через ось Oz;

· – плоскости, перпендикулярные оси Oz.

Якобиан отображения в цилиндрическую систему имеет вид

.

Тогда запись тройного интеграла в цилиндрических координатах

 

Пример 1. Перейти в тройном интеграле к цилиндрическим координатам и расставить пределы интегрирования, если

.

Решение

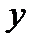
Рис. 7.22. Проекция тела на плоскость XOY

Область V − это часть цилиндра, ограниченного плоскостями (рис. 7.21). Проекцией на плоскость XOY будет часть окружности, ограниченной прямыми и (рис. 7.22).

y = x

z

x

Рис. 7.21. Часть цилиндра, ограниченного плоскостями

 

Уравнение цилиндра в цилиндрических координатах примет вид или . Следовательно, в области V координаты 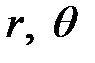и изменяются так: , , . Поэтому

= .

 

Пример 2. Вычислить тройной интеграл , где V – область, ограниченная поверхностями и .

Решение

z

х

у

или

Рис. 7.23. Область, ограниченная поверхностями и

Построим область, ограниченную поверхностями и (рис. 7.23).

 

7.3.4. вычисление тройного интеграла
в сферической системе координат

Положение точки М в пространстве можно определить, задав три величины:

1) расстояние r от этой точки до начала координат 0;

2) угол между координатной плоскостью Oxz и плоскостью, проходящей через точку М и ось Oz;

3) угол между радиусом-вектором и осью Oz (рис. 7.24).

При этом считают, что

Упорядоченная тройка чисел (r, называется сферическими координатами точки М. Связь с декартовыми координатами осуществляется при помощи формул

Сферические координаты тоже являются ортогональными. Координатными поверхностями здесь являются

· − сфера радиуса r;

· − плоскость, проходящая через ось Oz;

· − коническая поверхность с углом при вершине и с осью, совпадающей с Oz.

x

z

y

0

М

r

Рис. 7.24. Задание сферических координат

 

Якобиан отображения из декартовой в сферическую систему координат

 

 

Поэтому тройной интеграл в сферических координатах записывают в виде

 

Пример 1. Перейти в тройном интеграле к сферическим координатам и расставить пределы интегрирования

.

Решение

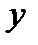
Рис. 7.25. Часть шара, лежащая вне конуса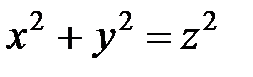

x

z

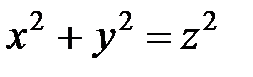Область V – это часть шара, ограниченная (вне) конусом (рис. 7.25). Уравнение сферы 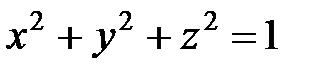в сферических координатах примет вид

или . Следовательно, в области V координаты и изменяются так: , , . Поэтому

= .

 

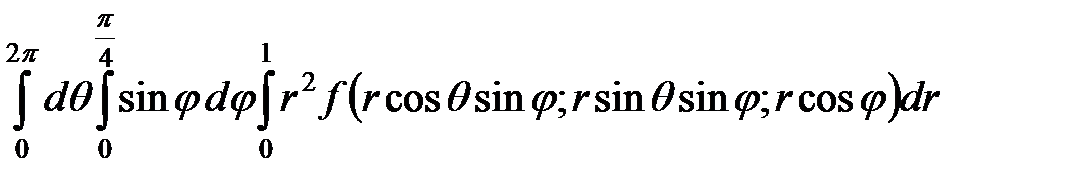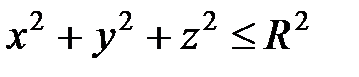Пример 2. Вычислить , если V – полушар и .

Решение

Переходим к сферическим координатам

Задания для самостоятельного решения

1. Подумайте, как запишется при аналогичной замене переменных двойной интеграл и коэффициент искажения элемента площади dS.

2. Перейдя к полярным координатам, вычислить , где область D – круг радиуса R = 1 с центром в начале координат. Ответ. .

3. Вычислить , где D − правая половина кольца между окружностями и 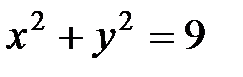. Ответ. .

4. Перейти в тройном интеграле к цилиндрическим координатам r, , z или сферическим координатам , , r и расставить пределы интегрирования:

 

а) ;

 

б) .

Ответ. а) ;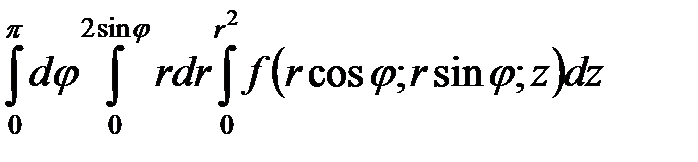

б) .

 

5. Вычислить тройной интеграл , если область V ограничена данными поверхностями:

 

а) ;

 

б) ;

 

в) .

Ответ. а) 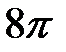; б) ; в) .

6. Переходя к сферическим координатам, вычислить тройной интеграл где V − шар радиуса R. Ответ. .

7.4. Механические приложения кратных интегралов

Пусть в пространстве R³ задано тело T с элементом объема dV (рис. 7.26). Тогда масса этого элемента может быть вычислена по формуле

,

где 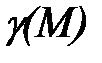– функция плотности. Тогда вся масса тела

.

 

z

x

y

x

z

y

T

M

dV

 

Рис. 7.26. Тело T в пространстве R³

 

Элементарный статический момент относительно плоскости хOу

.

Момент всего тела относительно плоскости х 0 у

.

Аналогично находятся моменты относительно других плоскостей:

,

.

Из механики известны формулы для вычисления координат центра тяжести тела

где m – масса тела; – статические моменты относительно плоскостей координат. Тогда

.

Аналогично вычисляются и .

Моменты инерции относительно осей координат соответственно равны:

,

,

.

 

Пример 1. Найти координаты центра тяжести тела, ограниченного плоскостями .

Решение

Найдем массу рассматриваемого тела

.

Тогда

;

;

.

 

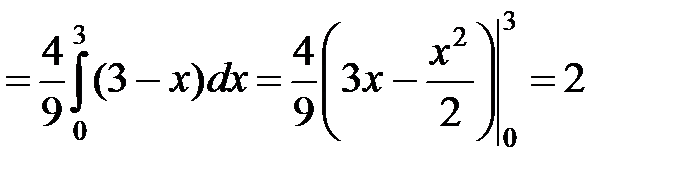Пример 2. Вычислить момент инерции фигуры, ограниченной кардиоидой , относительно оси Oх.

Решение

Перейдя к полярным координатам в формуле и полагая , получим

.

 

Задания для самостоятельного решения

1. Найти массу дуги окружности , ), если ее линейная плотность равна y. Ответ. 2.

2. Найти массу фигуры, ограниченной линиями , 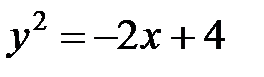. Ответ. 8.

3. Определить координаты центра тяжести фигуры, ограниченной линиями , , 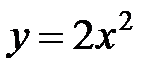, . Ответ. .

4. Найти массу куба 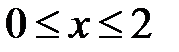, , , если плотность тела . Ответ. 24.

5. Найти координаты центра тяжести тела, ограниченного поверхностями 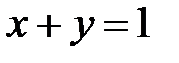, , 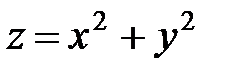, , . Ответ. .

 

Контрольные вопросы

по теме «Вычисление кратных интегралов»

 

1. Выясните геометрический смысл следующих двойных интегралов:

а) если

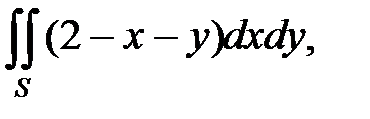б) если

2. Подумайте, при каком условии пределы интегрирования в формулах

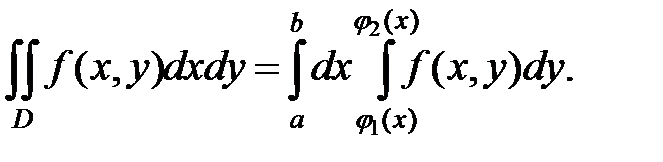
будут постоянными величинами.

3. Подумайте, при каком условии пределы интегрирования в формулах

,

будут постоянными величинами.

4. Подумайте, при каком условии пределы интегрирования в формуле

будут постоянными величинами.

5. Запишите формулу вычисления интеграла

в случае области V, правильной в направлении оси Oх, Оу.

6. Запишите координаты центра тяжести пластины, стержня.

 

 

 

[1] Якоби К. (1804-1851) – немецкий математик.