Проверочный расчет редуктора

 

Проверочный расчет зубьев шестерни на изгиб

 

Определим коэффициент формы зуба шестерни для эквивалентного числа зубьев при δ₁ = 36,2º

 

z_1э = z₁ / cos δ₁ = 73 / cos 36,2 = 90,5

 

По таблице для z_1э = 90,5, находим у_1э =.

 

Определим окружную скорость

 

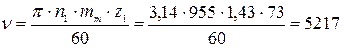мм/с = 5,22 м/с

 

Для 8 степени точности и υ = 5,22 < 10 м/с, k_ua = 1,35, k_uβ = 1, k_uυ = 1,4.

 

Находим поправочный коэффициент

 

k_u = k_ua ∙ k_uβ ∙ k_uυ = 1,35∙1∙1,14 = 1,89

 

Определим действительное число циклов

 

N₁ = 60∙n₁∙h = 60∙955∙40000 = 2,3∙10⁹ > 4∙10⁶,

 

поэтому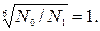

 

Определим допускаемое напряжение

 

[σ_u] = (1,8∙НВ / 1,75) ∙ 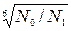= (1,8∙250 / 1,75) ∙ 1 = 257 Н/мм².

 

Делаем проверку прочности зубьев шестерни на изгиб

 

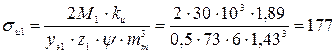Н/мм².

 

Запас прочности составляет [σ_u] / σ_u1 = 257 / 177 = 1,45 раза.

 

Проверочный расчет зубьев шестерни на контактную прочность

 

Находим поправочный коэффициент

 

k_u = k_ua ∙ k_uβ ∙ k_uυ = 1∙1∙1,2 = 1,2

 

Находим коэффициент контактных напряжений

 

С_н⁰ = (НВ – 100) / = (250 – 100) / 100 = 1,5 Н/мм²

 

Находим действительное число циклов перемены напряжений.

 

N = 60∙n₂∙h = 60∙694,5∙40000 = 1,7∙10⁹

 

т.к. N = 1,7∙10⁹ > N₀, то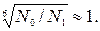

 

Находим допустимый коэффициент контактных напряжений

 

[C_н] = С_н⁰ ∙ 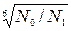= 1,5∙1 = 1,5 Н/мм²

 

Произведем проверочный расчет

 

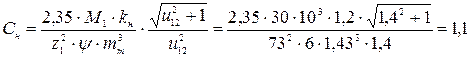< [C_н] = 1,5 Н/мм²

 

Запас прочности составляет [C_н] / С_н = 1,5 / 1,1 = 1,36 раза.

 

Проверочный расчет вала

 

Определим расстояние L₁, L₂, L₃ между опорными точками вала

 

L₃ = 0,5∙L_В2 + L_у2 + а = 0,5∙28 + 24 + 13 = 51 мм

 

где расстояние а находим по формуле

 

мм

 

L₂ = L_c2 + L_п2 –а – b = 89 + 25 – 13 – 9 = 92 мм

 

L₁ = В + L_Б2 –а – b = 89 + 28 – 13 – 9 = 95 мм

 

Строим эпюру крутящих моментов, если М_к = М₂ = 40,4 кН∙мм или М_к ≈ 41 кН∙мм

 

 

 

Рис. 1. Эпюра крутящих моментов

 

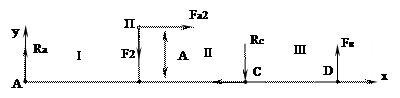
Разрабатываем расчетную схему

 

Вал изображаем как балку AD на двух опорах А и С. К балке приложены внешние силы: F_t, F_r2 и F_a2 в полюсе зацепления П, который жестко связан с балкой и составляет с ней единое целое, и тяговая сила F_в винтовой передачи в точке D. В опорах А и С будут возникать реакции. Радиальные реакции подшипников прикладывают к оси вала. Для радиально-упорных подшипников расстояние а между точкой приложения С и торцом подшипника определяется по формуле:

 

a = 0,5[B + 0,5(d+D)∙tg α] = 0,5[16 + 0,5(30 + 62)∙tg 12] = 13

 

Осевая реакция А прикладывается к подшипнику, на который давит сила F_a2 в точке С. Реакция А = F_a2. Складываем геометрически силы F_t и F_r2

 

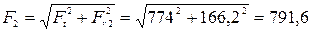Н

 

где F_t = 2∙M₂ / d_m1 = 2∙40,4∙013 / 104,4 = 774 Н

F_r2 = F_t ∙ tg α ∙ sin δ₁ = 774 ∙ tg 20 ∙ sin 36,2 = 166,2 Н

F_а2 = F_t ∙ tg α ∙ cos δ₁ = 774 ∙ tg 20 ∙ cos 36,2 = 227,4 Н

 

Полученную силу F₂ прикладываем в полюсе П. В полюсе П прикладываем и осевую точку F_а2.

Для определения радиальной реакции R_А составляем уравнение равновесия моментов от внешних сил, приложенных к балке. Равновесие рассматриваем относительно точки С, чтобы избавиться от реакции R_А.

 

∑М_с = F₂∙L₂ – F_a2∙r_m2 + F_в∙L₃ - R_A∙(L₁ + L₂) = 0,

 

откуда найдем искомую реакцию

 

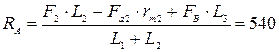Н = 0,54 кН.

 

Находим реакцию R_C, спроектировав силы на ось Y.

 

∑Y = R_A – F₂ + R_C + F_в = 0,

 

откуда

R_C = – R_A + F₂ – F_в = – 540 + 791,6 – 1250 = – 998 H ≈ – 1 кН

 

Спроектируем силы но ось Х

 

∑Х = F_а2 – А = 0,

 

 

откуда найдем осевую реакцию А опоры С

 

А = F_а2 = 227,4 Н.

 

 

 

	В

 

Рис. 2. Расчетная схема

 

6.3.4. Строим эпюру изгибающих моментов

 

1) Изгибающий момент на участке I

 

M_u1 = R_a∙x₁,

 

т.к. 0 ≤ x₁ ≤ L₁, то в точке А M_u1 = 0, а в точке В M_u1 = R_a∙L₁ = 540∙95 = 51300 Н∙мм ≈ ≈ 51 кН∙мм.

 

2) В точке В приложен сосредоточенный момент

 

m = F_a2∙r_m2 = 227,4∙84,7 = 19295 Н∙мм ≈ 19,3 кН∙мм.

 

В этой точке изгибающий момент M_u1 от первого участка скачком возрастает на величину m, т.е.

 

M_u2 = M_u1 + m = 51300 +19295 = 70595 Н∙мм ≈ 70,6 кН∙мм.

 

3) Изгибающий момент на участке III

 

M_u3 = F_в∙x₃,

 

т.к. 0 ≤ x₃ ≤ L₃, то в точке D M_u3 = 0, а в точке В M_u3 = F_в∙L₃ = 1250∙51 = 63750 Н∙мм ≈ ≈ 64 кН∙мм.

 

Mu2

Откладываем на эпюре контрольные точки в масштабе μ = 3,17 кН/мм и строим эпюру.

 

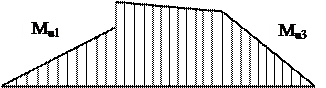Рис. 3. Эпюры изгибающих моментов

 

6.3.5. Намечаем опасные сечения

 

В соответствии с эпюрами изгибающих и крутящих моментов и размерами валов намечаем опасные сечения I-I и II-II. В этих сечениях моменты достигают максимальных значений и имеются концентраторы напряжений. В этих сечениях необходимо проверить вал на сопротивление усталости.

Проверку будем делать двумя методами: сопоставлением эквивалентного напряжения допускаемому, т.е.

 

σ_э = М_э / W ≤ [σ_-1]

 

и сопоставлением расчетного коэффициента запаса прочности допускаемому, т.е.

 

s = s_σ∙s_τ / .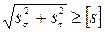

 

6.3.6. Определяем эквивалентные моменты в сечениях I-I и II-II

 

В сечении I-I по формуле

 

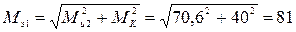кН∙мм

 

В сечении II-II по той же формуле

 

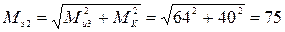кН∙мм

 

6.3.7. Находим осевые моменты сопротивления

 

В сечении I-I по таблице для диаметра d_ш2 = 32 мм W_х1 = 2730 мм³.

 

В сечении II-II по формуле

 

W_х2 = π∙d_п³ / 32 = 3,14∙30³ / 32 = 2650 мм³.

 

6.3.8. Определим комплексный коэффициент концентрации

 

В сечении I-I

 

ε = 0,88 – масштабный коэффициент для диаметра d_ш1 = 32 мм;

β = 1 – коэффициент, учитывающий шероховатость поверхности;

k_σ = 2,8 – коэффициент концентраций напряжений;

[n] = 2,1 – коэффициент запаса прочности;

комплексный коэффициент

 

k = ε ∙β / k_σ∙[n] = 0,88∙1 / 2,8∙2,1 = 0,15.

 

В сечении II-II

 

ε = 0,88 – масштабный коэффициент для диаметра d_ш1 = 32 мм;

β = 1 – коэффициент, учитывающий шероховатость поверхности;

k_σ = 2,1 – коэффициент концентраций напряжений;

[n] = 2,1 – коэффициент запаса прочности;

комплексный коэффициент

 

k = ε ∙β / k_σ∙[n] = 0,88∙1 / 2,1∙2,1 = 0,2.

 

6.3.9. Определим допускаемое напряжение от изгиба с кручением

 

[σ_-1] = k∙σ_-1,

 

где = 380 Н/мм² – предельное напряжение при симметричном цикле для стали 45

 

В сечении I-I

 

[σ_-1] = 0,15∙380 = 57 Н/мм²

 

В сечении II-II

 

[σ_-1] = 0,2∙380 = 76 Н/мм²

 

6.3.10. Проверяем прочность вала

 

В сечении I-I

 

σ_э1 = М_э1 / W_х1 = 81000 / 2730 =29,7 Н/мм² < [σ_-1] = 57 Н/мм²

 

В сечении II-II

 

σ_э2 = М_э2 / W_х2 = 75000 / 2650 = 28,3 Н/мм² < [σ_-1] = 76 Н/мм²

 

В обоих сечениях прочность удовлетворительна

 

6.3.11. Определяем полярные моменты сопротивления

 

В сечении I-I по таблице для диаметра d_ш2 = 32 мм W_р1 = 5940 мм³.

 

В сечении II-II по формуле

 

W_р2 = π∙d_п³ / 16 = 3,14∙30³ / 16 = 5300 мм³.

 

6.3.12. Определяем амплитуды нормальных напряжений при симметричном

цикле

 

В сечении I-I

 

σ_а1 = М_u1 / W_р1 = 70600 / 5940 =13,4 Н/мм²

 

В сечении II-II

 

σ_а2 = М_u2 / W_р2 = 64000 / 5300 = 12,1 Н/мм²

 

6.3.13. Определяем амплитуды нормальных напряжений при отнулевом цикле

 

В сечении I-I

 

τ_а1 = τ_max / 2 = М_к / 2∙W_р1 = = 40000 / 2∙5940 = 3,4 Н/мм²

 

В сечении II-II

 

τ_а2 = τ_max / 2 = М_к / 2∙W_р2 = 40000 / 2∙5300 = 3,8 Н/мм²

 

6.3.14. Коэффициент концентраций напряжений

 

В сечении I-I

 

k_υ = 1 – коэффициент влияния поверхностного уплотнения;

k_υd = 3,46 для диаметра d_ш2 = 32 мм и σ_в = 800 Н/мм² – коэффициент, учитывающий концентрацию напряжений и влияние диаметра сечения;

k_F = 1 – коэффициент влияния шероховатости поверхности

коэффициент концентрации нормальных напряжений

 

k_σ1 = (k_υd + k_F – 1) / k_υ = (3,46 + 1 – 1) / 1 = 3,46

 

k_υd = 2,48 для диаметра d_ш2 = 32 мм и σ_в = 800 Н/мм² – коэффициент, учитывающий концентрацию напряжений и влияние диаметра сечения;

коэффициент концентрации касательных напряжений

 

k_τ1 = (k_υd + k_F – 1) / k_υ = (2,48 + 1 – 1) / 1 = 2,48

 

В сечении II-II

 

k_υ = 1 – коэффициент влияния поверхностного уплотнения;

k_υd = 3,43 для диаметра d_п2 = 30 мм и σ_в = 800 Н/мм² – коэффициент, учитывающий концентрацию напряжений и влияние диаметра сечения;

k_F = 1 – коэффициент влияния шероховатости поверхности

коэффициент концентрации нормальных напряжений

k_σ2 = (k_υd + k_F – 1) / k_υ = (3,43 + 1 – 1) / 1 = 3,43

 

k_υd = 2,46 для диаметра d_п2 = 30 мм и σ_в = 800 Н/мм² – коэффициент, учитывающий концентрацию напряжений и влияние диаметра сечения;

коэффициент концентрации касательных напряжений

 

k_τ2 = (k_υd + k_F – 1) / k_υ = (2,46 + 1 – 1) / 1 = 2,46

 

6.3.15. Определяем коэффициенты запаса прочности по нормальным и касательным напряжениям

 

В сечении I-I

 

s_σ1 = σ_-1 / σ_a1 ∙ k_σ1 = 260 / 13,4 ∙ 3,46 = 5,6

 

где σ_-1 = 260 Н/мм²

 

s_τ1 = τ_-1 / τ_a1 ∙ k_σ1 = 150 / 3,4 ∙ 2,48 = 17,8

 

где τ_-1 = 150 Н/мм²

 

В сечении II-II

 

s_σ2 = σ_-1 / σ_a2 ∙ k_σ2 = 260 / 12,1 ∙ 3,43 = 6,3

 

s_τ2 = τ_-1 / τ_a2 ∙ k_σ2 = 150 / 3,8 ∙ 2,46 = 16

 

6.3.16. Проверяем условие прочности вала

 

В сечении I-I

 

> [s] = 2,1,

 

В сечении II-II

 

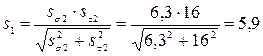> [s] = 2,1.

 

6.3.17. Определим действительные запасы прочности вала

 

Метод эквивалентного напряжения:

В сечении I-I

 

n₁ = [σ_-1]₁ / σ_э1 = 57 / 29,7 = 1,9,

 

В сечении II-II

 

n₁ = [σ_-1]₁ / σ_э2 = 76 / 28,3 = 2,7.

 

Метод расчетного коэффициента запаса прочности:

В сечении I-I

 

n₁ = s₁ / [s] = 5,3 / 2,1 = 2,5,

 

В сечении II-II

 

n₂ = s₂ / [s] = 5,9 / 2,1 = 2,8.

 

Если взять среднее значение допускаемого коэффициента запаса прочности

[s]_ср = (1,3 + 2,1) / 2 = 1,7, то получим:

 

В сечении I-I

 

n₁ = s₁ / [s]_ср = 5,3 / 1,7 = 3,1,

 

В сечении II-II

 

n₂ = s₂ / [s]_ср = 5,9 / 1,7 = 3,5.

 

Простым сравнением можно прийти к выводу, что оба метода дают близкие по точности результаты и могут применяться для проверочных расчетов вала.

 

Проверочный расчет подшипников

 

Определим отношение

 

А / С₀ = 227,4 / 12000 = 0,019,

 

согласно которому находим методом интерполяции коэффициент е = 0,34.

 

6.4.2. Подшипник в опоре А нагружен только радиальной силой R_А, а в опоре С радиальной силой R_С и осевой – А. Т.к. R_А < R_С, то расчету подлежит подшипник в опоре С, учитывая, что этот подшипник нагружен еще осевой силой. Для опоры С определяем отношение А / R_С = 227,4 / 998 = 0,23 < е = 0,34. В этом случае Х = 1,

Y = 0.

 

6.4.3. Определяем эквивалентную нагрузку подшипника С

 

Q_С = R_С ∙ k_Б ∙ k_Т = 988∙1,4∙1 = 1383 Н ≈ 1,4 кН.

 

6.4.4. Находим номинальную долговечность более нагруженного подшипника

 

L = a∙(C / Q_С)^m = 0,7∙(22 / 1,4)³ = 2716 ч.

 

6.4.5. Рассчитываем базовую долговечность

 

L_h = 10⁶∙L / 60n = 10⁶∙2716 / 60∙694,5 = 65200 > [L_h] = 10000ч,

 

что больше требуемой долговечности.

 

Заключение

 

В данной курсовой работе был произведен расчет конического редуктора. Был произведен подбор электродвигателя для данного редуктора, рассчитаны геометрические и кинематические параметры механизма. Произведен силовой расчет механизма. Также произведены расчеты основных размеров зубьев и корпуса редуктора.

Над полученным редуктором был произведен проверочный расчет. Конические зубчатые колеса были проверены на изгиб и на контактную прочность. Также были рассчитаны на прочность валы и подшипники.

Проверочных расчеты показали, что полученный редуктор обладает большой прочностью.

Также в курсовой работе были выполнены графические работы.

 

 

Список используемой литературы

 

1. Дунаев П.Ф., Леликов О.П. Детали машин. Курсовое проектирование. М.: Высшая школа, 1990.

2. Решетов Д.Н. Детали машин: Учебник для ВУЗов М.: Высшая школа, 1982.

3. Руппель А.И. Основы механики: Программа, методические указания и контрольные задания. Омск: Изд-во СибАДИ, 2001.

4. Руппель А.И. Краткий курс механики: Учебное пособие. Омск: Изд-во

СибАДИ, 2003.

5. Цехнович Л.И. Атлас конструкций редукторов. Киев: Высшая школа, 1990.