Учимся решать физические задачи
Относительность движения
Нельзя наблюдать и определить
движение тела, имеющего конечную
величину, не определяя сначала,
какое движение имеет каждая его
маленькая частичка или точка.
Л. ЭЙЛЕР
Расчет средней скорости переменного движения
В предыдущих номерах журнала уже разбирались некоторые методы и подходы к решению задач по кинематике. Но вступительные экзамены в высшие учебные заведения показали, что задачи на расчет средней скорости неравномерного движения по-прежнему решаются неверно очень многими учащимися. Затруднения вызывают и задачи, в которых решение значительно упрощается переходом в удобную систему отсчета. Поэтому мы еще раз возвращаемся к вопросам кинематики и предлагаем учащимся 9-11 классов внимательно отнестись к предложенным темам..
Итак, движения разделяются:
¨ по характеру траектории – на прямолинейное и криволинейное;
¨ по наличию ускорения – на равномерное, переменное и равнопеременное.
 Равномерное прямолинейное движение – это движение с постоянной скоростью, то есть V = const, a = 0. Обратите внимание, что скорость постоянна и по модулю и по направлению.
Равномерное прямолинейное движение – это движение с постоянной скоростью, то есть V = const, a = 0. Обратите внимание, что скорость постоянна и по модулю и по направлению.
Переменное движение может быть прямолинейным и криволинейным. Одной из характеристик прямолинейного переменного движения является средняя путевая скорость, которую часто называют просто средней скоростью движения. Для определения средней скорости движения мы истинное сложное движение мысленно заменяем равномерным движением, при котором тот же путь проходится за то же время.
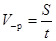 , где S – весь пройденный путь, t – все время движения.
, где S – весь пройденный путь, t – все время движения.
Обратите внимание, что в физике вводятся два различных понятия средней скорости: векторная средняя скорость, вычисляемая по вектору перемещения тела за определенное время движения Vср = S /t, и скалярная средняя скорость, определяемая длиной пути вдоль траектории, которую мы и называем путевой скоростью. По модулю эти скорости не совпадают, поэтому при решении задач желательно уточнять, о какой средней скорости ведется речь. В приведенных ниже примерах мы будем иметь в виду путевую среднюю скорость. Но иногда в задачах движение задается графиком скорости. Вот тогда уточнение того, о какой средней скорости идет речь, обязательно.
Обратите внимание на еще один момент в вычислении средней скорости неравномерного движения.
Только в том случае, когда тело движется прямолинейно с постоянным ускорением а, возможно применение формулы Vср = (V1 + V2)/2. Объясняется это тем, 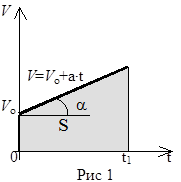 что на графике скорости прямолинейное движение с постоянным ускорением (равнопеременное движение) (рис. 1) может быть представлено линейной зависимостью скорости от времени V = V0 + at
что на графике скорости прямолинейное движение с постоянным ускорением (равнопеременное движение) (рис. 1) может быть представлено линейной зависимостью скорости от времени V = V0 + at
Так как площадь под графиком скорости численно равна длине пути S за промежуток времени от 0 до t1, то для равноускоренного движения по формуле площади трапеции находим S = (Vо+V)·t1/2. Отсюда сравнением с формулой расчета длины пути S=Vср t1 получаем формулу для расчета средней скорости прямолинейного равнопеременного движения Vср = (V0 + V)/2 или Vср = (V1 + V2)/2, где V1 и V2 соответственно скорости в начале и в конце прямолинейного участка движения.
То есть мы фактически заменили данное движение равномерным со скоростью Vср и площадью под линией графика, равной пройденному пути S (рис. 2) 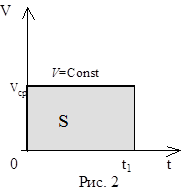
Если же не выполняется хотя бы одно из оговоренных условий: либо движение не прямолинейное, либо скорость зависит от времени не линейно (то есть движение не равнопеременное), применять выведенную выше формулу расчета средней скорости Vср = (V1 + V2)/2 нельзя!
В таком случае необходимо пользоваться общей формулой расчета средней скорости Vср = åS/åt,
где åS – весь пройденный телом путь, åS = S1 + S2 + S3+ S4 + …,
åt – все время движения, включая остановки; åt = t1+ t2+ t3+ t4+…
Среднюю скорость можно определять и по графику зависимости пути от времени (рис 3)
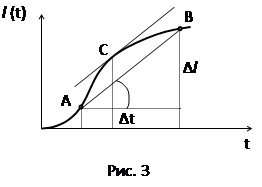 Средняя скорость, равная Vср = Δl / Δt, на этом графике определяется тангенсом угла наклона прямой, соединяющей начальную и конечную точки рассматриваемого участка движения, к оси времени. По этому графику легко можно судить об изменении средней скорости в зависимости от выбора интервала времени. Кроме того, можно определить тот момент времени, когда мгновенная скорость будет по модулю равна средней скорости на заданном участке движения. Для этого нужно параллельным переносом полученного отрезка АВ до касания с линией графика найти точку касания С. Ее координаты и будут соответствовать искомому моменту времени и пройденному к этому моменту времени пути.
Средняя скорость, равная Vср = Δl / Δt, на этом графике определяется тангенсом угла наклона прямой, соединяющей начальную и конечную точки рассматриваемого участка движения, к оси времени. По этому графику легко можно судить об изменении средней скорости в зависимости от выбора интервала времени. Кроме того, можно определить тот момент времени, когда мгновенная скорость будет по модулю равна средней скорости на заданном участке движения. Для этого нужно параллельным переносом полученного отрезка АВ до касания с линией графика найти точку касания С. Ее координаты и будут соответствовать искомому моменту времени и пройденному к этому моменту времени пути.
Задача 1. Первую четверть пути автомобиль двигался со скоростью 30 км/ч, вторую четверть - со скоростью 40 км/ч, а оставшийся путь - со скоростью 80 км/ч. Определить среднюю скорость движения автомобиля на всем пути.
| Дано: S1=1/4 S S2=1/4 S S3=1/2 S V 1=30 км/ч V 2=40 км/ч V 3=80 км/ч | Решение.

|
| V ср =? | Средняя скорость движения равна V ср= 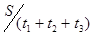 . .
|
Здесь t1 = 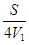 ; t2 =
; t2 =  ; t3 =
; t3 = 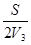 .
.
Получаем (t1 + t2 + t3) = 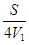 +
+  +
+ 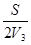 =
=  .
.
Тогда V ср= 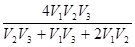 ; V ср=
; V ср= 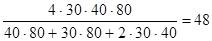 км/ч.
км/ч.
Ответ: средняя скорость движения автомобиля 48 км/ч.
Примечание. Еще раз обратите внимание на расчет средней скорости движения. При неравномерном движении ни в коем случае нельзя рассчитывать среднюю скорость как среднюю арифметическую скорость. Решая подобную задачу, учащиеся часто допускают ошибку, рассчитывая среднюю скорость как 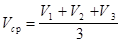 , что совершенно не допустимо!
, что совершенно не допустимо!
Задача 2. Автомобиль двигался по ровной дороге 1 мин со скоростью 90 км/ч, а затем 2 мин на подъеме со скоростью 60 км/ч и под уклон 0,5 мин со скоростью 120 км/ч. Определить среднюю скорость движения автомобиля за это время.
| Дано: t1=1=1/60 ч V 1=90 км/ч t2=2 мин=1/30 ч V 2=60 км/ч t3=0,5 мин=1/120 ч V 3=120 км/ч | Решение.Средняя скорость движения автомобиля равна
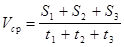 , где S1= V 1*t1; S2= V 2*t2; S3= V 3*t3.
Получаем , где S1= V 1*t1; S2= V 2*t2; S3= V 3*t3.
Получаем 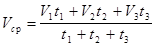 . Подставив данные, получаем
V ср=77 км/ч. . Подставив данные, получаем
V ср=77 км/ч.
|
| V ср -? | Ответ: средняя скорость движения автомобиля 77 км/ч. |
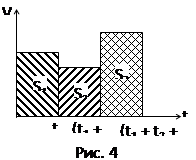 Примечание. 1.Эту задачу можно решать и графически с помощью графика скорости. Для этого необходимо построить в одной системе координат (V, t) графики скорости для каждого интервала времени, затем рассчитать весь пройденный путь как площадь под общим графиком за весь промежуток времени (рис. 4).
Примечание. 1.Эту задачу можно решать и графически с помощью графика скорости. Для этого необходимо построить в одной системе координат (V, t) графики скорости для каждого интервала времени, затем рассчитать весь пройденный путь как площадь под общим графиком за весь промежуток времени (рис. 4).
Средняя скорость может быть найдена отношением всего пройденного пути ко всему промежутку времени 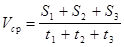 .
.
Задача 3. Велосипедист проехал первую половину пути со скоростью 12 км/ч, а второю половину пути – со скоростью 20 км/ч. Определить среднюю скорость движения велосипедиста.
| Дано: S1=S2=1/2 S V 1=12 км/ч V 1=20 км/ч | Решение. Средняя скорость движения велосипедиста равна
V ср=  , где t1= , где t1= 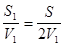 , t2= , t2= 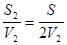 . Тогда (t1+t2)= . Тогда (t1+t2)= 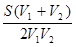 . .
|
| V ср-? | 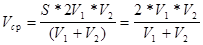 ; ; 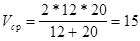 км/ч. км/ч.
|
Ответ: средняя скорость движения велосипедиста 15 км/ч.
Задача 4. Первую половину времени велосипедист двигался со скоростью 12 км/ч, а вторую половину времени – со скоростью 20 км/ч. Определить среднюю скорость велосипедиста за все время движения.
| Дано: t1=t2=1/2 t V 1=12 км/ч V 1=20 км/ч | Решение. Средняя скорость движения велосипедиста равна 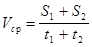 , где , где 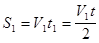 ; ; 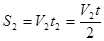 ; t=t1+t2. Тогда S1+S2= ; t=t1+t2. Тогда S1+S2= 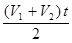
|
| V ср-? | 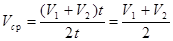 ; V ср=16 км/ч. ; V ср=16 км/ч.
|
Ответ: средняя скорость движения велосипедиста 16 км/ч.
Примечание. Обратите внимание на разницу в условиях задачи № 3 и № 4 и разные значения средней скорости. При этом подход к решению и в том и в другом случаях одинаков.