Для описания точек геометрических объектов с помощью чисел и написания уравнений задают систему координат. Существуют различные системы координат: декартова, полярная, криволинейная и другие. Будем рассматривать наиболее употребительную — декартову систему координат на плоскости.
 |
Декартова система координат может быть прямоугольной и косоугольной. В дальнейшем будем рассматривать декартову прямоугольную систему. На плоскости это две взаимно перпендикулярные числовые оси (Рис. 1 Декартова система координат на плоскости).
Рис. 1 Декартова система координат на плоскости
Декартовыми координатами точки на плоскости называется упорядоченная пара чисел, являющихся проекциями точки на оси координат.
Запись: М(х;у), где х — первая координата, абсцисса, у —вторая координата, ордината.
 |
Декартова прямоугольная система координат в пространстве — это три взаимно перпендикулярные числовые оси (Рис. 2. Декартова система координат в пространстве).
Рис. 2. Декартова система координат в пространстве
Декартовыми координатами точки в пространстве называется упорядоченная тройка чисел, являющихся проекциями точки на оси координат.
Запись: М(х; у; z), где х — абсцисса, у — ордината, z — аппликата.
|
Уравнением линии на плоскости 0xy называются уравнения F(х; у) = 0 или y = f(x), которым удовлетворяют координаты x и y любой точки, лежащей на линии и не удовлетворяют координаты всякой точки не лежащей на ней.
Если дано уравнение, то можно сказать, что линия, определенная уравнением в некоторой системе координат, это геометрическое место точек (ГМТ), координаты которых удовлетворяют уравнению.
|
|
Уравнение прямой на плоскости в декартовых координатах может записываться по-разному, в зависимости от условий.
1. Уравнение прямой с угловым коэффициентом.
 |
Здесь: k = tg α — угловой коэффициент прямой, α — угол наклона прямой к оси х, b — ордината точки пересечения прямой с осью у (Рис. 3 Прямая в декартовых координатах).
Рис. 3 Прямая в декартовых координатах
2. Уравнение прямой, проходящей через данную точку (х1; у1) в данном направлении (с данным углом наклона к оси х).
3. Уравнение прямой, проходящей через две данные точки (х1; у1) и (х2; у2).

4. Уравнение прямой «в отрезках» (Рис. 4 Прямая, отсекающая на осях отрезки а и b).

 |
Рис. 4 Прямая, отсекающая на осях отрезки а и b
5. Общее уравнение прямой: Ax+By+C=0
В MS Excel 2010 для построения прямых, а также кривых и поверхностей, производится с помощью диаграмм.
 |
Пример 1. Построить график функции (Рис. 5)
на отрезке [-5;5] с шагом 0,5
6. Определим функцию f(x). Для этого в ячейки А1:А21 необходимо ввести значение аргумента при помощи автозаполнения, в данном случае с шагом 0,5. В ячейку В1 вводится значение функции, вычисляемое по формуле =(A1^2*(A1+3))^(1/3). Ячейки В2:В21 заполняются копированием формулы из ячейки В1 (Для изменения названия столбцов войдите в Меню Файл - Параметры - Формулы и снимите галку с Стиль ссылок R1C1)
7. Далее выделим диапазон А1:В21 и построим диаграмму, отображающую график функции. Чтобы создать базовую диаграмму, нужно выбрать нужный тип диаграммы на вкладке Вставка.
8. Для построения графика функции лучше выбрать точечную диаграмму с гладкими кривыми.
|
|
9. Чтобы график получился выразительным, можно определить промежуток изменения аргумента, выделить оси координат, нанести на них соответствующие деления, сделать подписи на осях и вывести заголовок.
Для редактирования подписи делений горизонтальной оси:
· Выделите область диаграммы.
· Перейдите на вкладку Макет и на панели Текущий фрагмент в списке Область диаграммы выберите Горизонтальная ось (категорий).
· Ниже выберите Формат выделенного.
· Установите Параметры оси: минимальное значение – (-5); максимальное – (5); цена основных делений – (0,5); Тип линии: ширина – (1,5); Цвет линии: черный.
· С помощью контекстного меню добавьте основные линии сетки.
Проведите аналогичные действия для форматирования вертикальной оси.
10. С помощью инструментов на панели Подписи вкладки Макет введите название диаграммы и отключите отображение легенды (Рис. 5)
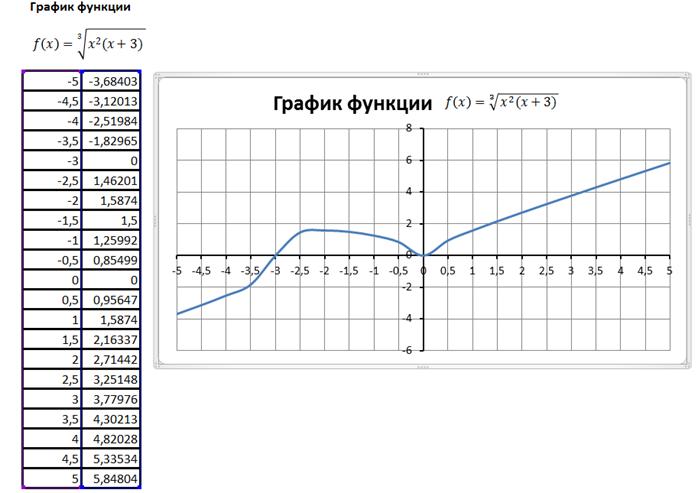
Рис. 5
Пример 2.Построить график функции

При построении этого графика следует обратить внимание на область определения функции. В данном случае функция не существует при обращении знаменателя в ноль.

Следовательно, при определении значений аргумента следует помнить, что при х=-2 функция не определена. На рис. 6. видно, что значение аргумента задано в два этапа, не включая (-2) с шагом 0,2(
Рис. 6).
Рис. 6
Пример 3Построить график функции

|
Здесь подкоренное выражение не должно быть отрицательным:

Определение значения аргумента следует провести в два этапа. Например, от -5 до -1, а затем от 1 до 5,с шагом 0,1.
Пример 4Построить график функции:

|
При построении этого графика следует использовать функцию ЕСЛИ. Например, в ячейке А1 (Рис. 7) находится начальное значение аргумента, тогда в ячейку В1 необходимо ввести формулу:
|
|
=ЕСЛИ(A1<0;1+A1;ЕСЛИ(A1>=1;A1^2;EXP(A1))).
 Рис. 7
Рис. 7
Пример 5Изобразите линию, заданную неявно уравнением
 .
.
Заметим, что заданная уравнением f(x,y)=0 функция описывает кривую линию под названием эллипс.
В связи с тем, что линия задана неявно, для ее построения необходимо разрешить заданное уравнение относительно переменной y:


После проведенных преобразований можно увидеть, что линию f(x,y) можно изобразить, построив графики двух функций в одной графической области.

Перед построением определим область допустимых значений функций f 1 (x) и f 2 (x).
Поскольку эти функции содержат в числителе выражение под знаком квадратного корня, то обязательным условием их существования будет выполнение следующего неравенства:

Теперь перейдем к построению графика.
Для этого в диапазон А3:А43 введем значения аргумента (от -2 до 2 с шагом 0,1).
В ячейку В3 введем формулу для вычисления значений функции f 1 (x):
=КОРЕНЬ(20-5*$A3^2)/2.
А в ячейку С3 для вычисления значений функции f 2 (x):
= - КОРЕНЬ(20-5*$A3^2)/2.
Далее скопируем эти формулы до В43 и С43 соответственно.
Затем выделим диапазон А3:С43 и построим графики функций f 1 (x) и f 2 (x) в одной графической области (Рис. 8)

Рис. 8
ВАРИАНТЫЗАДАНИЙ
ЗАДАНИЕ 1. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) |
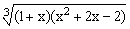
| 
| 
| |||

| 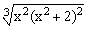
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||
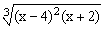
| 
| 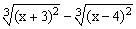
| |||

| 
| 
| |||

| 
| 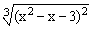
|
ЗАДАНИЕ 2. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) |
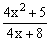
| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 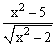
| |||

| 
| 
| |||

| 
| 
|
ЗАДАНИЕ 3. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) |

| 
| 
| |||

| 
| 
| |||

| 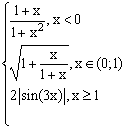
| 
| |||

| 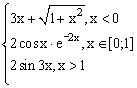
| 
| |||

| 
| 
| |||
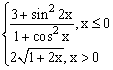
| 
| 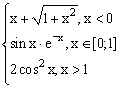
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
|
ЗАДАНИЕ 4. Изобразите линии заданные неявно уравнением f(x,y)=0.
| № | f(x) | № | f(x) | № | f(x) |
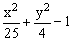
| 
| 
| |||

| 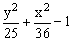
| 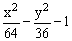
| |||
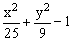
| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
|