Гиперболический параболоид

Глава 1.

Определение декартовой системы координат.

Декартова система координат в пространстве определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенныечерез начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1). Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов , , , , , отличен от нуля.

Типы поверхностей второго порядка

Цилиндрические поверхности

Поверхность называется цилиндрической поверхностью с образующей , если для любой точки этой поверхности прямая, проходящая через эту точку параллельно образующей , целиком принадлежит поверхности .

Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность имеет уравнение , то — цилиндрическая поверхность с образующей, параллельной оси .

Кривая, задаваемая уравнением в плоскости , называется направляющей цилиндрической поверхности.

Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.

Эллиптический цилиндр:	Параболический цилиндр:	Гиперболический цилиндр:
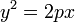
Пара совпавших прямых:	Пара совпавших плоскостей:	Пара пересекающихся плоскостей:

Конические поверхности

Коническая поверхность.

4

Поверхность называется конической поверхностью с вершиной в точке , если для любой точки этой поверхности прямая, проходящая через и , целиком принадлежит этой поверхности.

Функция называется однородной порядка , если выполняется следующее:

Теорема (об уравнении конической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность задана уравнением , где — однородная функция, то — коническая поверхность с вершиной в начале координат.

Если поверхность задана функцией , являющейся однородным алгебраическим многочленом второго порядка, то называется конической поверхностью второго порядка.

§ Каноническое уравнение конуса второго порядка имеет вид:

Поверхности вращения

Поверхность называется поверхностью вращения вокруг оси , если для любой точки этой поверхности окружность, проходящая через эту точку в плоскости с центром в и радиусом , целиком принадлежит этой поверхности.

Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность задана уравнением , то — поверхность вращения вокруг оси .

Эллипсоид:	Однополостной гиперболоид:	Двуполостной гиперболоид:	Эллиптический параболоид:

В случае, если , перечисленные выше поверхности являются поверхностями вращения.

Гиперболический параболоид

Гиперболический параболоид.

Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

Уравнение гиперболического параболоида:

При сечении гиперболического параболоида плоскостью поверхность порождает гиперболу.

При сечении гиперболического параболоида плоскостью или поверхность порождает параболу.