КОНЕЧНОЗНАЧНЫЕ СИНГУЛЯРНЫЕ ФУНКЦИИ
Функция Хевисайда
При изучении распространения сигнала по проводам Оливер Хевисайд в конце XIX века ввел функцию включения
 (3.1)
(3.1)


На рисунках функция  включается в точке
включается в точке  , где
, где  . При
. При  функция
функция  , при
, при 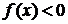 функция
функция  . Из рисунков получаем
. Из рисунков получаем
 . (3.2)
. (3.2)
Из нормировки дельта-функции следует
 ,
,
тогда
 ,
,
 , (3.3)
, (3.3)
где использовано дифференцирование интеграла по пределу
если  , то
, то  ;
;
если  , то
, то  .
.
Из (3.1) получаем
 ,
,
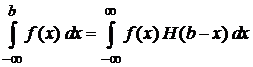 . (3.4)
. (3.4)
С учетом (3.4) находим свертку
 .
.
Меняем знак аргумента функции  и используем (3.4)
и используем (3.4)
 .
.
Дифференцируем последние соотношения
 ,
,
 . (3.5)
. (3.5)
Функция знака аргумента
От лат. sīgnum – «знак»
 (3.11)
(3.11)

Свойства
Функция нечетная
 ,
,
 . (3.12)
. (3.12)
Выполняется
 ,
,
кроме точки  .
.
Связь с функцией Хевисайда и дельта-функцией
Графически получаем
 , (3.13)
, (3.13)
откуда
 . (3.13а)
. (3.13а)
Графически находим
 , (3.13б)
, (3.13б)
тогда с учетом (3.3)
 ,
,
 ,
,
получаем
 . (3.14)
. (3.14)
Фурье-образ
Используем (1.1)
 ,
,
где для сходимости интегралов при  введено
введено
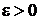 ,
,  .
.
Используем
 ,
,
 ,
,
получаем фурье-образ функции знака
 . (3.19)
. (3.19)
Из (3.19) и (3.13), (2.35) в виде
 ,
,
 ,
,
получаем фурье-образ функции Хевисайда
 . (3.20)
. (3.20)
Используем теорему Фурье о парах функций:
если  ,
,
то  .
.
С учетом (3.19) полагаем
 ,
,  ,
,
тогда
 .
.
Используем (3.12) и (3.13а)
 ,
,
 ,
,
получаем
 . (3.21)
. (3.21)
Прямоугольная функция
Прямоугольная функция  симметричная, имеет единичную ширину, и скачок единичной величины при
симметричная, имеет единичную ширину, и скачок единичной величины при  :
:
 (3.27)
(3.27)

Произвольная прямоугольная функция

имеет ширину b и высоту h. Она симметрична относительно точки c, как показано на рисунке.

Координату  оси симметрии находим из условия на аргумент функции
оси симметрии находим из условия на аргумент функции
 ,
,
получаем
 .
.
Координаты  точек скачка находим из условий на аргумент функции
точек скачка находим из условий на аргумент функции
 ,
,
получаем
 .
.
Ширина функции
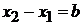 .
.
Свойства
Функция четная
 ,
,
имеет значения 0 или 1, тогда
 ,
,
 ,
,  (3.28)
(3.28)
Связи с другими функциями
Используя графики функций, самостоятельно доказать:
 ,
,
 ,
,
 ,
,
 . (3.29)
. (3.29)
Выполняется
 .
.
Доказательство
Сравниваем положения точек скачка функций. Для 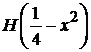 находим
находим
 ,
,  .
.
Результат совпадает со скачками  . При
. При  обе функции равны единице. При
обе функции равны единице. При 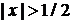 обе функции равны нулю.
обе функции равны нулю.
Фурье-образ
Используем (1.1) и (3.27)
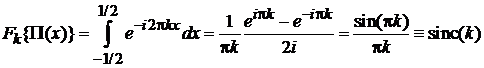 ,
,
получаем
 . (3.31)
. (3.31)
Используя (3.31) и (1.1), (1.2) доказать самостоятельно
 , (3.32)
, (3.32)
 . (3.33)
. (3.33)
Функция sink
Название от термина «синус»
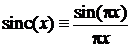 . (3.35)
. (3.35)
Согласно (3.31) является Фурье-образом прямоугольной функции
 .
.
Оптическое преобразование Фурье, осуществляемое тонкой линзой, как описано на одной из первых лекциях, применяем к функции  . Она моделирует щель шириной 1, через которую идет световая волна, как показано на рисунке. Функция
. Она моделирует щель шириной 1, через которую идет световая волна, как показано на рисунке. Функция  описывает амплитуду дифрагированной волны на щели единичной ширины.
описывает амплитуду дифрагированной волны на щели единичной ширины.

Дифракция на щели
Для щели шириной A получаем
 , (3.35а)
, (3.35а)
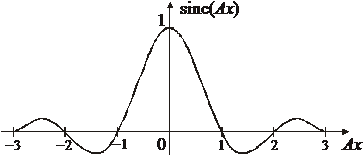
Чем шире щель, тем ближе к началу координат нули функции sink, и наоборот, в соответствии с теоремой Фурье о частотной полосе.
Функция четная
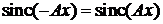 .
.
Нули функции при
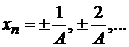
Выполняется
 ,
, 
Из (3.35) с учетом «замечательного предела» получаем
 . (3.36)
. (3.36)
Числовой расчет дает положения и величины экстремумов
| | x| | 1,43 | 2,46 | 3,47 | |

| –0,22 | 0,13 | –0,09 |
Фурье-образ
Спектр  является прямоугольной функцией, равной единице в полосе
является прямоугольной функцией, равной единице в полосе  и нулю вне этой полосы
и нулю вне этой полосы
 . (3.41а)
. (3.41а)
Доказательство
Используем теорему Фурье о парах функций:
если  ,
,
то  .
.
Полагаем
 ,
,
используя (3.31)
 ,
,
берем
 .
.
Учитываем
 ,
,
и получаем (3.41а).
Доказать самостоятельно
 . (3.41б)
. (3.41б)
При  из (3.41б) следует, что функция
из (3.41б) следует, что функция 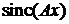 имеетспектр равный единице в полосе
имеетспектр равный единице в полосе  , и нулевой вне этой полосы.
, и нулевой вне этой полосы.
Из (3.41б) при 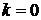 получаем
получаем
 ,
,
 . (3.38)
. (3.38)
Площадь под кривой  равна единице.
равна единице.
Из (3.32)
 ,
,
при 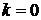 находим
находим
 . (3.37)
. (3.37)
Усреднение функции
Среднее  по интервалу Т около точки x равно сумме значений функции в указанном интервале, деленное на ширину интервала.
по интервалу Т около точки x равно сумме значений функции в указанном интервале, деленное на ширину интервала.
Усреднение определяется в виде
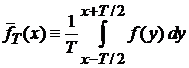 . (3.42)
. (3.42)
Используем (3.27)

находим

Получена прямоугольная функция величиной 1 в интервале шириной T с центром в точке a. Вне этого интервала функция равна нулю. При  получаем интервал интегрирования в (3.42), тогда
получаем интервал интегрирования в (3.42), тогда
 .
.
Последний интеграл является сверткой, тогда
 . (3.42а)
. (3.42а)
Усреднение функции по интервалу шириной Т является сверткой этой функции с прямоугольной функцией шириной Т.
Фурье-образ усредненной функции
При усреднении функции по интервалу Т ее Фурье-образ модулируется функцией 
 . (3.42б)
. (3.42б)
Чем меньше интервал усреднения, тем сильнее меняется спектр при удалении от точки 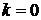 .
.
Доказательство
Используем (3.42а)
 .
.
По теореме Фурье о свертке (1.24)
 ,
,
с учетом (3.32)
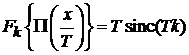
получаем (3.42б).
Треугольная функция
Обозначается буквой Λ – «лямбда» греческого алфавита
 (3.43)
(3.43)
Площадь под графиком функции равна единице
 .
.
