Понятие числовой функции

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ и фун-ия

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f (x), x Î N,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f (n)или y 1, y 2,…, y_n,…. Значения y 1, y 2, y 3,…называют соответственно первым, вторым, третьим, … членами последовательности.

Например, для функции y = n 2_\shad \shad0можно записать:

y 1 = 1² = 1;/// y 2 = 2² = 4;/// y 3 = 3² = 9;… y_n = n 2;…

Способы задания последовательностей. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.

1. Последовательность задана аналитически, если задана формула ее n -го члена:

y_n = f (n).

Пример. y_n = 2 n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательныйспособ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….

Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.

3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n -й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n -й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.

Пример 1. y 1 = 3; y_n = y_n –1 + 4, если n = 2, 3, 4,….

Здесь y 1 = 3; y 2 = 3 + 4 = 7; y 3 = 7 + 4 = 11; ….

Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: y_n = 4 n – 1.

Пример 2. y 1 = 1; y 2 = 1; y_n = y_n –2 + y_n –1, если n = 3, 4,….

Здесь: y 1 = 1; y 2 = 1; y 3 = 1 + 1 = 2; y 4 = 1 + 2 = 3; y 5 = 2 + 3 = 5; y 6 = 3 + 5 = 8;

Понятие числовой функции

Пусть задано числовое множество Если каждому числу поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция:

y = f (x),

Множество D называется областью определения функции и обозначается D (f (x)). Множество, состоящее из всех элементов f (x), где 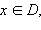называется областью значений функции и обозначается E (f (x)).

Число x часто называют аргументом функции или независимой переменной, а число y – зависимой переменной или, собственно, функцией переменной x. Число соответствующее значению называют значением функции в точке 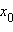и обозначают или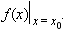

Для того чтобы задать функцию f, нужно указать:

1) ее область определения D (f (x));

2) указать правило f, по которому каждому значению ставится в соответствие некоторое значение y = f (x).

2)Предел числовой последовательности.
Предел также является одним из основных понятий математики. Если данная функция y =f (x) при определённом изменении x приближается к некоторой постоянной величине c, то последняя называется пределом функции f (x). Точный смысл понятия «предел функции» имеет лишь при указании закона изменения x и наличия точного понятия близости элемента y к величине c. С пределом связаны основные понятия математического анализа: непрерывность, производная,дифференциал, интеграл. Одним из простейших случаев предела функции является предел числовой последовательности.

Предел числовой последовательности. Пусть дана числовая последовательность – функция f, ставящая каждому натуральному числу n из множества натуральных чисел N в соответствие определенный элемент y из множества действительных чисел R, который обозначим как

Действительное число c называется пределом последовательности , если для любого действительного числа ε > 0 существует такое число N, что для всех натуральных n >N выполняется неравенство , при этом пишут . Здесь указано, что n берутся достаточно большими, а близость y к c определяется модулем их разности.

Предел функции. Пусть функция f ставит каждому числу x из некоторого подмножества действительных чисел R в соответствие действительное число y =f (x). Действительное число b называется пределом функции f в точке a из R (при x стремящемся к a), если для любого действительного числа ε > 0 существует такое действительное число δ > 0, что для любого такого числа x, что 0 < | x –a | < δ, выполняется неравенство | f (x) –b | < ε, при этом пишут Отметим, что в определении требуется, чтобы функция f была определена для чисел x, близких к a.