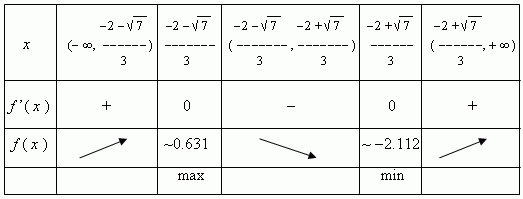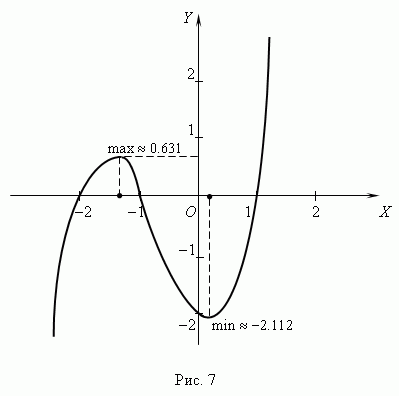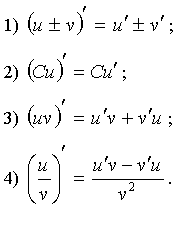
20. Геометрический смысл производных.
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.
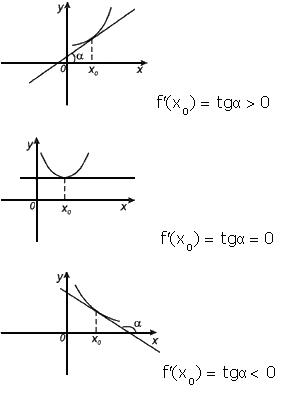
Рассмотрим график функции y = f (x):
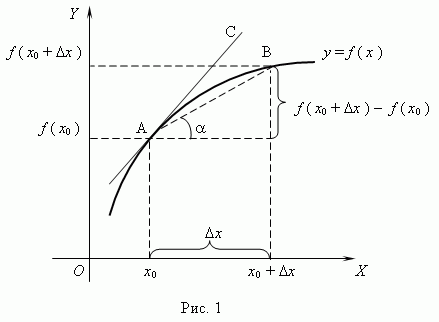
Из рис.1 видно, что для любых двух точек A и B графика функции: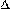 
xf (x 0+ 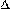x)− f (x 0)= tg 
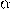, где 
- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то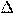 
x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует:производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
21. Производная сложной функции.
"Двухслойная" сложная функция записывается в виде
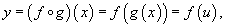где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция  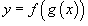также дифференцируема по x и ее производная равна
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".
|
| Пример 1 |
Найти производную функции  .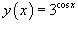
Решение.
Поскольку 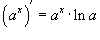 , то по правилу производной сложной функции получаем
|
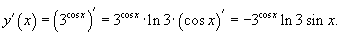
22. Дифференцируемая функция. Дифференциал
Пусть функция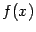 
задана в некоторой област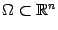и 
, и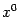 
-- внутренняя точка этой области. Пусть 
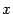-- произвольная точка этой же области 
. Разность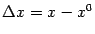 
называется приращением аргумента ; 
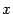, где 
. Разность значений функции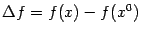 
называется приращением, или полным приращением функции 
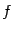в точке 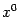, соответствующим приращению аргумента 
; 
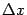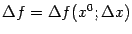-- это функция от точки 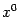и приращения .
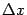Предположим, что приращение функции можно представить в виде
| (7.2) |
где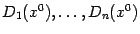 
-- некоторые числа. Подчеркнём, что эти числа не зависят от 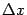, но могут измениться, если сменить точку 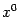. Относительно величины 
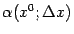мы предположим, что это функция, при базе 
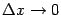являющаяся величиной большего порядка малости, чем 
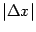. Это означает, если вспомнить определение бесконечно малой величины большего порядка малости относительно другой бесконечно малой, что
Заметим, что сумма всех слагаемых левой части (7.2), кроме последнего, -- это линейная функция от приращения аргумента 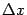, если точка 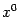фиксирована. Условие большей малости последнего слагаемого (7.2) относительно 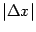означает, что эта линейная функция -- главная часть приращения функции.
Определение 7.11 Если указанное представление (7.2) имеет место, то функцию 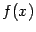называют дифференцируемой в точке 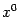, а линейную относительно 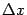функцию
то есть главную линейную часть приращения функции, -- дифференциалом функции 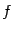в точке .
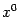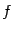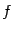Если функция является дифференцируемой в любой точке открытой области , то функцию называют дифференцируемой в области .
Таким образом, приращение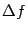 
дифференцируемой функции можно представить в виде суммы дифференциала 
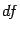, то есть линейной части приращения, и остатка 
, который имеет более высокий порядок малости, чем приращение :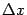
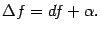
23. Теорема о дифференцируемости функции
Теорема. Для того, чтобы функция f (x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она имела производную в этой точке. При этом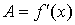 
, 
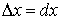и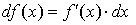 
.
Геометрический смысл дифференциала изображен на рис. 3.5. Заметьте, что производная есть отношение дифференциала функции к дифференциалу независимой переменной:
.
Это – самая обычная дробь.
Рис. 3.5 Геометрический смысл дифференциала.
24. Теоритический смысл дифференциала
25. Св-ва дифференциалов.
Выражение производной через дифференциалы:
где индекс "х" при y' показывает, что производная берется по аргументу х. В то же время дифференциалы dy и dx можно брать по любому аргументу.
Выражение дифференциала через производную:
Используя его, можно записать свойства дифференциалов, используя свойства производной.
1. Постоянный множитель можно вынести за знак дифференциала:
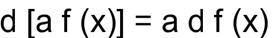
2. дифференциал алгебраической суммы функций равен алгебраической сумме дифференциалов этих функций
3. дифференциал произведения
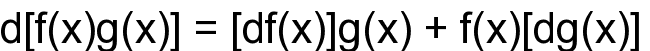
4. дифференциал дроби (дифференциал частного)
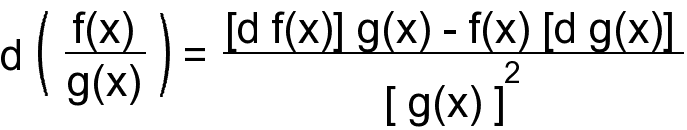
5. дифференциал сложной функции
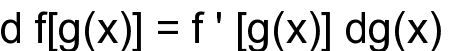
где d g(x), в свою очередь, можно дифференцировать дальше.
26. Производные и дифференциалы высших порядков.
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,
f" (x) = (f' (x)) '.
Если дифференцируема (n - 1)-я производная функции f, то ее n -й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n) (x) = (f(n-1) (x)) ', n ϵ N, f(0) (x) = f (x).
Число n называется порядком производной.
Дифференциалом n -го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf (x) = d (dn -1 f (x)), d 0 f (x) = f (x), n ϵ N.
Если x - независимая переменная, то
dx = const и d 2 x = d 3 x =... = dnx = 0.
В этом случае справедлива формула
dnf (x) = f (n)(x)(dx) n.
Производные n -го порядка от основных элементарных функций
Справедливы формулы
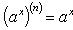
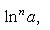
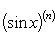
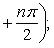
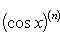
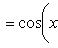
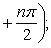
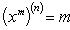
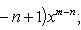
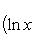
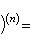
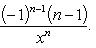
Формула Лейбница
Если u и v - n -кратно дифференцируемые функции, то
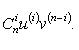
Производные n -го порядка вектор-функции, комплекснозначной и матричной функций
Если компоненты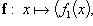 
n -кратно дифференцируемы, то 
.
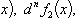
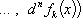Аналогично для комплекснозначной функции f и матричной функции A имеем формулы:
f (n)(x) = u (n)(x) + iv (n)(x); dnf (x) = dnu (x) + idnv (x);
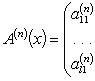
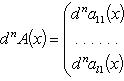
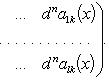
27. Применение производных для исследования функций.
План исследования функции. Для построения графика функции нужно:
1) найти область определения и область значений функции,
2) установить, является ли функция чётной или нечётной,
3) определить, является ли функция периодической или нет,
4) найти нули функции и её значения при x = 0,
5) найти интервалы знакопостоянства,
6) найти интервалы монотонности,
7) найти точки экстремума и значения функции в этих точках,
8) проанализировать поведение функции вблизи “особых” точек
и при больших значениях модуля x.
П р и м е р. Исследуйте функцию f (x) = x 3 + 2 x 2 - x - 2 и постройте график.
Р е ш е н и е. Исследуем функцию по вышеприведенной схеме.
1) область определения x 
R (x – любое действительное число);
область значений y R, так как f (x) – многочлен нечётной
степени;
2) функция f (x) не является ни чётной, ни нечётной
(поясните, пожалуйста);
3) f (x) – непериодическая функция (докажите это сами);
4) график функции пересекается с осью Y в точке (0, – 2),
так как f (0) = - 2; чтобы найти нули функции нужно
решить уравнение: x 3 + 2 x 2 - x - 2 = 0, один из корней
которого (x = 1) очевиден. Другие корни находятся
(если они есть!) из решения квадратного уравнения:
x 2 + 3 x + 2 = 0, которое получено делением многочлена
x 3 + 2 x 2 - x - 2 на двучлен (x – 1). Легко проверить,
что два других корня: x 2 = -2 и x 3 = -1. Таким образом,
нулями функции являются: -2, -1 и 1.
5) Это значит, что числовая ось делится этими корнями на
четыре интервала знакопостоянства, внутри которых
функция сохраняет свой знак:
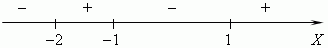
Этот результат может быть получен разложением
многочлена на множители:
x 3 + 2 x 2 - x - 2 = (x + 2) (x + 1 (x – 1)
и оценкой знака произведения методом интервалов
(см. раздел «Неравенства» в главе «Алгебра»).
6) Производная f’ (x) = 3 x 2 + 4 x -1 не имеет точек, в которых
она не существует, поэтому её область определения R (все
действительные числа); нули f’ (x) – это корни уравнения:
3 x 2 + 4 x - 1 = 0.
Полученные результаты сведены в таблицу:
