| §1 Матрицы | |||||
| 1. Матрица, элементы матрицы | Прямоугольная таблица, составленная из  чисел, называется матрицейиз чисел, называется матрицейиз  строк и строк и  столбцов размера столбцов размера 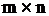 . Для обозначения матрицы применяются круглые скобки и прописные буквы А, В, С..... Числа . Для обозначения матрицы применяются круглые скобки и прописные буквы А, В, С..... Числа 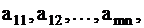 составляющие матрицу, называются ее элементами. Горизонтальные ряды матрицы называются строками матрицы, вертикальные - столбцами. составляющие матрицу, называются ее элементами. Горизонтальные ряды матрицы называются строками матрицы, вертикальные - столбцами.
|  А=
А=  – матрица размера – матрица размера 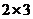 .
1, 2, 3 – элементы первой строки. 3,5 – элементы третьего столбца. Элемент .
1, 2, 3 – элементы первой строки. 3,5 – элементы третьего столбца. Элемент  =3. =3.
| |||
| 2. Симметрическая матрица | Если amn = anm, то матрица называется симметрической |  - симметрическая матрица - симметрическая матрица
| |||
| 3. Квадратная матрица. Главная и побочная диагонали квадратной матрицы. | Матрица, у которой число строк равно числу ее столбцов называется квадратной матрицей. При этом число ее строк (столбцов) называется порядком матрицы.
В квадратной матрице числа  образуют главную диагональ матрицы, а числа образуют главную диагональ матрицы, а числа  побочную диагональ. побочную диагональ.
| 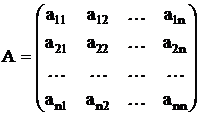 Матрица
Матрица  есть квадратная матрица третьего порядка. 1,0,7 – элементы главной диагонали. есть квадратная матрица третьего порядка. 1,0,7 – элементы главной диагонали.
| |||
| 4. Диагональная матрица | Квадратная матрица, у которой все числа, не стоящие на главной диагонали, равны нулю, называется диагональной матрицей. | Квадратная матрица вида  называется диагональнойматрицей. называется диагональнойматрицей.
 – диагональная матрица второго порядка. – диагональная матрица второго порядка.
| |||
| 5. Единичная матрица | Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Единичную матрицу обозначают прописной буквой Е | Матрица вида  , называется единичной матрицей. , называется единичной матрицей.
| |||
| 6. Матрица-строка, матрица-столбец. | Матрица, состоящая только из одной строки, называется матрицей-строкой, состоящая только из одного столбца матрицей - столбцом. | Матрица А=(2 0 5 4) есть матрица – строка.
В =  – матрица – столбец. – матрица – столбец.
| |||
| 7. Транспониро- ванная матрица | Матрица  называется транспонированнойпо отношению к матрице А, если столбцы (строки) матрицы называется транспонированнойпо отношению к матрице А, если столбцы (строки) матрицы  являются соответствующими строчками (столбцами) матрицы являются соответствующими строчками (столбцами) матрицы  . .
|  ; ; 
| |||
| 8. Равенство матриц | Две матрицы А и В называются равными(A=B), если они имеют одинаковые размеры и равные соответствующие элементы. | Если  и и  , то , то 

| |||
| 9. Сумма матриц | Пусть даны матрицы  и и  , имеющие одинаковые размеры , имеющие одинаковые размеры  .
Суммой матриц А и В называется матрица .
Суммой матриц А и В называется матрица  тех же размеров тех же размеров  , что и заданные матрицы, элементы которой , что и заданные матрицы, элементы которой 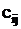 определяются правилом определяются правилом 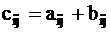 для всех для всех  .
Сумма матриц подчиняется переместительному и сочетательному законам, т.е. .
Сумма матриц подчиняется переместительному и сочетательному законам, т.е.  и и 
| Задача.
Если  то то
 Задача.
Даны матрицы
Задача.
Даны матрицы  ; ;  , найти 2А + В.
Решение. , найти 2А + В.
Решение.
 , , 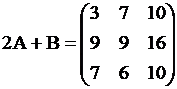 . .
| |||
| 10. Умножение матрицы на число | Произведением матрицы  размеров размеров  на число на число 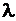 называется матрица называется матрица  тех же размеров, что и матрица А, элементы, которой определяются правилом тех же размеров, что и матрица А, элементы, которой определяются правилом  для всех для всех 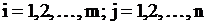 .
Умножение матрицы на число подчиняется закону .
Умножение матрицы на число подчиняется закону  , где , где 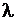 и и  числа. числа.
| Задача.
Если 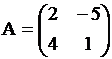 и и  , то , то 
| |||
| 11. Умножение матриц | Произведением матрицы А размеров  на матрицу В размеров на матрицу В размеров  называется матрица называется матрица  размеров размеров  , элементы , элементы  которой определяются по формуле (1.4) для всех которой определяются по формуле (1.4) для всех  и всех и всех  . .
| Задача.
Даны 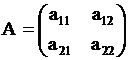 и и  Так как число столбцов матрицы А равно числу строк матрицы В, то произведение
Так как число столбцов матрицы А равно числу строк матрицы В, то произведение  определено и определено и
 .
Задача.
Даны .
Задача.
Даны  , ,  .
Решение.
Матрица А имеет два столбца, В - две строки; следовательно, .
Решение.
Матрица А имеет два столбца, В - две строки; следовательно,  определено. определено.
 . .
| |||
| §2 Определители | |||||
| 12. Понятие определителя. Определитель второго порядка. | Определитель –это число, которое по специальным правилам вычисляется для каждой квадратной матрицы.
Определителем второго порядка, соответствующим заданной матрице А, называется число равное  Для обозначения определителя используются вертикальные черточки и прописная буква
Для обозначения определителя используются вертикальные черточки и прописная буква 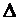 . .
| 

| |||
| 13. Определитель третьего порядка | Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число

 Элементы
Элементы  образуют главную диагональ определителя, а элементы образуют главную диагональ определителя, а элементы  побочную диагональ. побочную диагональ.
| Задача.
Вычислить определитель матрицы  Решение.
Решение.

 . .
| |||
| 14. Минор | Минором  элемента элемента  , где , где  определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием  й строки и й строки и  го столбца. го столбца.
|  Задача.
Дано:
Задача.
Дано:  . Найти . Найти 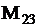 .
Решение. .
Решение.
 .
Ответ. – 2. .
Ответ. – 2.
| |||
| 15. Алгебраическое дополнение | Алгебраическим дополнением  элемента элемента  , где , где  , называется минор , называется минор  этого элемента, взятый со знаком этого элемента, взятый со знаком  . .  где где  . .
|  Задача.
Дано:
Задача.
Дано:  . Найти . Найти  .
Решение. .
Решение.
 .
Ответ. 2. .
Ответ. 2.
| |||
16.Определители
 го порядка го порядка
| Определитель 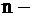 го порядка, соответствующий квадратной матрице А, обозначается символом го порядка, соответствующий квадратной матрице А, обозначается символом
 и определяется как число
и определяется как число
 где
где  есть миноры соответствующих элементов есть миноры соответствующих элементов  т.е. определители т.е. определители  го порядка, полученные из данного вычеркиванием его первой строки и соответственно первого, второго,..., го порядка, полученные из данного вычеркиванием его первой строки и соответственно первого, второго,...,  го его столбцов. го его столбцов.
| Пример. Вычислить определитель  . .
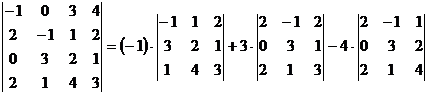 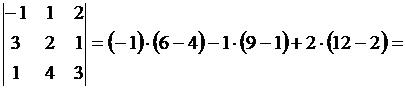
 . .
 . .

 .
Значение определителя: .
Значение определителя:  . .
| |||
| 17. Понятие вырожденной и невырожденной матрицы | Обозначим через 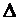 определитель матрицы определитель матрицы  и вычислим его. Тогда, если и вычислим его. Тогда, если  , то матрицу , то матрицу  называют неособенной (невырожденной) матрицей, если же называют неособенной (невырожденной) матрицей, если же  , то особенной (вырожденной) матрицей. , то особенной (вырожденной) матрицей.
|  . .

 .
Так как .
Так как  , то матрица , то матрица  невырожденная. невырожденная.
| |||
| 18. Обратная матрица | Квадратная матрица  порядка порядка  называется обратной матрицей для данной матрицы называется обратной матрицей для данной матрицы  , если , если
 где
где  единичная матрица.
Всякая неособенная матрица единичная матрица.
Всякая неособенная матрица  имеет обратную матрицу имеет обратную матрицу  , определяемую формулой , определяемую формулой
 ,
где ,
где  есть алгебраические дополнения соответствующих элементов есть алгебраические дополнения соответствующих элементов  матрицы матрицы  . .
| Задача.
Дана матрица  , найти , найти  .
Решение.
det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, .
Решение.
det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом,  . .
| |||
| 19. Ранг матрицы | Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается  или или  . Очевидно, что . Очевидно, что  , где , где  меньшее из чисел меньшее из чисел  и и  . Минор, порядок которого определяет ранг матрицы, называется базисным. . Минор, порядок которого определяет ранг матрицы, называется базисным.
| Задача.
Дана матрица  . Определить ее ранг. Решение.
Имеем . Определить ее ранг. Решение.
Имеем 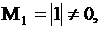  , ,  .
Минор четвертого порядка составить нельзя.
Ответ. .
Минор четвертого порядка составить нельзя.
Ответ. 
| |||
| 20. Определение ранга матрицы методом элементарных преобразований | Простейший способ определения ранга матрицы состоит в приведении ее к ступенчатому виду при помощи последовательности элементарных преобразований. К ним относятся: - умножение строки на произвольное число, отличное от нуля; - прибавление к некоторой строке любой другой строки, умноженной на одно и тоже число; - вычеркивание нулевой строки. | Задача.
Найти ранг матрицы  .
Решение.
После вычитания первой строки из остальных получаем эквивалентную матрицу, а из последней умноженную на 2, .
Решение.
После вычитания первой строки из остальных получаем эквивалентную матрицу, а из последней умноженную на 2,  .
Поскольку три строки промежуточной матрицы были пропорциональны, то из них можно получить две ненулевые строки, которые мы отбросили. Ясно, что .
Поскольку три строки промежуточной матрицы были пропорциональны, то из них можно получить две ненулевые строки, которые мы отбросили. Ясно, что  т.к. т.к. 
| |||
| 21. Совместная и несовместная система линейных уравнений. Определенная и неопределенная система линейных уравнений. Теорема Кронекера – Капелли. | Система, имеющая хотя бы одно решение, называется совместной, имеющая только одно решение определенной, имеющая более одного решения - неопределенной,не имеющая ни одного решения - несовместной. Теорема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений. | Задача.
Определить совместность системы линейных уравнений:


 Ранг A = 2
Ранг A = 2
 Ранг
Ранг  . Система несовместна. . Система несовместна.
| |||
| 22. Решение системы линейных уравнений по формулам Крамера | Теорема. Система из n уравнений с n неизвестными
 в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di /D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di /D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.

 ; ;
 ; ;
 ; ;
 ; ;
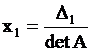 ; ; 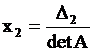 ; ;  . .
| Задача.
Решить по формулам Крамера систему уравнений
 Решение.
Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель
Решение.
Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель 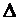 этой системы. этой системы.
 Так как
Так как  ,то решение можно найти по формулам Крамера: ,то решение можно найти по формулам Крамера:
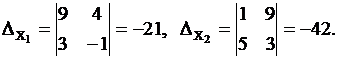 Тогда Тогда
 Ответ. {1;2}.
Ответ. {1;2}.
| |||
| 23. Решение систем линейных уравнений матричным методом |  Задача.
Решить матричным способом систему уравнений
Задача.
Решить матричным способом систему уравнений
 Решение.
Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель
Решение.
Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель 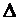 этой системы: этой системы:  . Так как . Так как  , то система может быть решена матричным способом. Составим матрицы , то система может быть решена матричным способом. Составим матрицы 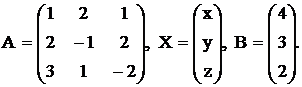 Так как определитель системы Так как определитель системы  , то матрица , то матрица  имеет обратную матрицу имеет обратную матрицу  , где , где  Вычислим алгебраические дополнения Вычислим алгебраические дополнения  всех элементов всех элементов
 Тогда
Тогда  . .
| ||||
| 24. Решение систем линейных уравнений методом Гаусса. | Метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
 Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения;
2) умножим на а31 и вычтем из третье и т.д.
Получим:
Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения;
2) умножим на а31 и вычтем из третье и т.д.
Получим:
 ,
где ,
где  , j = 2, 3, …, n+1. , j = 2, 3, …, n+1.
 , i = 2, 3, …, n;
j = 2, 3, …, n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д. , i = 2, 3, …, n;
j = 2, 3, …, n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
| Задача.
Решить систему методом Гаусса.
 Решение.
Составим расширенную матрицу системы.
Решение.
Составим расширенную матрицу системы.
 Таким образом, исходная система может быть представлена в виде:
Таким образом, исходная система может быть представлена в виде:
 ,
откуда получаем: z = 3; y = 2; x = 1. ,
откуда получаем: z = 3; y = 2; x = 1.
| |||
| 25. Вектор. Координаты вектора. | Вектором называется направленный отрезок. Пусть точка  есть начало вектора, а точка есть начало вектора, а точка  его конец, тогда этот вектор обозначается символом его конец, тогда этот вектор обозначается символом  и изображается с помощью стрелки.
Если заданы 2 точки в пространстве и изображается с помощью стрелки.
Если заданы 2 точки в пространстве  и и  , то , то  . .
|  Задача.
Дано: Задача.
Дано:  , , 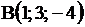 . Найти координаты вектора . Найти координаты вектора  .
Решение. .
Решение.
 , ,
 .
Ответ. .
Ответ.  . .
| |||
| 26. Модуль вектора | Расстояние между началом и концом вектора называется длиной вектораили его модулем. Модуль вектора обозначается символами  Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве  , ,  , то , то  .
Если .
Если  , то , то  . .
| Задача.
Дано:  , , 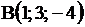 . Найти . Найти  .
Решение. .
Решение.
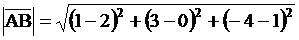 , ,
 , ,
 .
Ответ. .
Ответ.  . .
| |||
| 27. Нулевой вектор | Вектор, начало которого совпадает с его концом, называется нулевым и обозначается  . Нулевой вектор не имеет определенного направления и его . Нулевой вектор не имеет определенного направления и его  . .
| 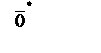 

| |||
| 28. Понятие коллинеарных векторов | Векторы, расположенные на одной прямой или параллельных прямых, называются коллинеарными.
Пусть векторы  и и  заданы в координатной форме: заданы в координатной форме: 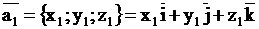 , ,

 . .  -условие коллинеарности двух векторов -условие коллинеарности двух векторов
| Задача.
При каких  и и  векторы векторы  и и 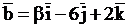 коллинеарны?
Решение.
Так как коллинеарны?
Решение.
Так как  , то , то  .
Отсюда находим, что .
Отсюда находим, что  ; ;  . .
| |||
| 29. Понятие компланарных векторов | Векторы, расположенные на одной плоскости или на параллельных плоскостях, называются компланарными. | 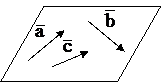 векторы
векторы  , ,  , ,  - компланарные. - компланарные.
| |||
| 30. Понятие равенства векторов | Два вектора  и и  называются равными, если они коллинеарны, одинаково направлены и имеют одинаковую длину. Равенство векторов записывается в виде называются равными, если они коллинеарны, одинаково направлены и имеют одинаковую длину. Равенство векторов записывается в виде  . В координатной форме: . В координатной форме:
 , если , если  . .
|  


| |||
| 31. Противопо- ложный вектор | Вектор 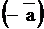 называется противоположным вектором для вектора называется противоположным вектором для вектора  , если он ему коллинеарен, имеет одинаковую с , если он ему коллинеарен, имеет одинаковую с  длину, но направлен в противоположную сторону. Векторы длину, но направлен в противоположную сторону. Векторы  и и  называются взаимно-противоположными векторами. называются взаимно-противоположными векторами.
| 
 
| |||
| 32. Единичный вектор | Вектор, длина которого равна единице, называется единичным вектором и обозначается символом  . .
| Задача.
(Координаты единичного вектора).
Определить координаты единичного вектора  , если , если  .
Решение. .
Решение.
 
 ,
следовательно, ,
следовательно,
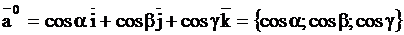 . .
| |||
| 33. Сумма векторов | Суммой векторов  и и  называется третий вектор называется третий вектор  , начало которого совпадает с началом вектора , начало которого совпадает с началом вектора  , а конец – с концом вектора , а конец – с концом вектора  , при условии, что начало вектора , при условии, что начало вектора  приложено к концу вектора приложено к концу вектора  .
Пусть векторы .
Пусть векторы  и и  заданы в координатной форме: заданы в координатной форме:
 Сумма векторов:
Сумма векторов:  . .
|
Задача. Дано: Решение.
Ответ.
| |||
| 34. Разность векторов | Разностью векторов  и и  называется такой вектор называется такой вектор  , что , что  .
Разность векторов в координатной форме: .
Разность векторов в координатной форме:

|  Задача.
Дано: Задача.
Дано:  , ,  . Найти . Найти  .
Решение. .
Решение.
 , ,
 .
Ответ. .
Ответ.  . .
| |||
| 35. Деление отрезка в данном отношении | Если точка  делит отрезок делит отрезок  , где , где 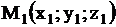 , ,  в отношении в отношении 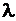 , т.е. , т.е.  , то ее координаты находятся по формулам , то ее координаты находятся по формулам
 , , 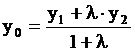 , ,
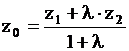 .
В частности, при .
В частности, при 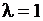 точка точка  делит отрезок пополам делит отрезок пополам  , ,  , ,  . .
| Задача.
Даны точки  и и  . На прямой . На прямой 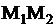 найти точку найти точку  , делящую отрезок , делящую отрезок 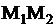 в отношении в отношении  .
Решение. .
Решение.
 , ,
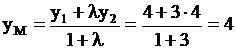 , ,
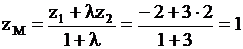 .
Следовательно, искомая точка .
Следовательно, искомая точка  .
Ответ. .
Ответ.  . .
| |||
| 36. Проекция вектора на ось |
Проекция вектора  на ось на ось  равна модулю вектора равна модулю вектора  , умноженному на косинус угла , умноженному на косинус угла  между вектором и осью: между вектором и осью:
| Задача.
Вычислить проекцию вектора  на направление вектора на направление вектора  .
Решение. .
Решение.

 , ,  Следовательно,
Следовательно,  .
Ответ. .
Ответ.  . .
| |||
| 37. Скалярное произведение векторов | Скалярным произведениемвекторов  и и  называется число, равное произведению длин этих сторон на косинус угла между ними. называется число, равное произведению длин этих сторон на косинус угла между ними.
 Свойства скалярного произведения:
1)
Свойства скалярного произведения:
1)  ;
2) ;
2)  , если , если  или или  , или , или  .
3) .
3)  ;
4) ;
4)  ;
5) ;
5)  , ,  .
Если рассматривать векторы .
Если рассматривать векторы  ; ;  в декартовой прямоугольной системе координат, то в декартовой прямоугольной системе координат, то  . .
| Задача.
Найти скалярное произведение  , если , если  Решение.
Решение.

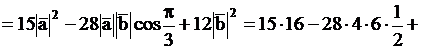
 .
Ответ. 336. .
Ответ. 336.
| |||
| 38. Определение угла между векторами. Геометрический смысл скалярного произведения векторов. | Так как  , то , то

| Задача.
Даны вершины треугольника  и и  . Определить внутренний угол треугольника при вершине . Определить внутренний угол треугольника при вершине  . .
 Решение.
Построим векторы
Решение.
Построим векторы  и и  . Имеем . Имеем  . Тогда . Тогда

 Ответ.
Ответ. 
| |||
| 39.Ортогональность векторов | Если  то то  или или
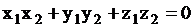 .
Условие называется условием перпендикулярности двух векторов .
Условие называется условием перпендикулярности двух векторов
| Задача.
При каком m векторы  и и  перпендикулярны.
Решение. перпендикулярны.
Решение.
 ; ; 
 .
Ответ. .
Ответ. 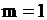 . .
| |||
| 40. Направляющие косинусы вектора | Обозначим через  углы, между вектором углы, между вектором  и осями координат и осями координат  . Тогда из прямоугольных треугольников . Тогда из прямоугольных треугольников 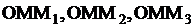 получим получим
 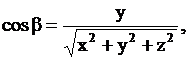
  . .
| Задача.
Вектор  задан координатами своих концов: задан координатами своих концов:  и и  . Найти проекции вектора . Найти проекции вектора  на координатные оси и его направляющие косинусы.
Решение.
Находим проекции вектора на координатные оси и его направляющие косинусы.
Решение.
Находим проекции вектора  на координатные оси: на координатные оси:  , ,
 , ,  , а модуль вектора , а модуль вектора  . Вычислим направляющие косинусы: . Вычислим направляющие косинусы:
 ; ;  ; ;  .
Ответ. .
Ответ.  ; ;  ; ;  . .
| |||
| 41. Физический смысл скалярного произведения векторов | Задача.
Вычислить работу по перемещению материальной точки вдоль отрезка, из точки  в точку в точку  под действием постоянной по величине и направлению силы под действием постоянной по величине и направлению силы 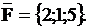 Решение.
Из курса физики известно, что работа
Решение.
Из курса физики известно, что работа  , совершаемая при указанных в примере условиях, находится по формуле , совершаемая при указанных в примере условиях, находится по формуле 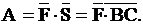 Так как Так как  , то , то
 Ответ. 5.
Ответ. 5.
| ||||
| 42. Векторное произведение векторов | Векторным произведениемвекторов  и и  называется вектор называется вектор  , удовлетворяющий следующим условиям: 1) , удовлетворяющий следующим условиям: 1)  , где , где  - угол между векторами - угол между векторами  и и  ; 2) вектор ; 2) вектор  ортогонален векторам ортогонален векторам  и и
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2018-03-19 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |

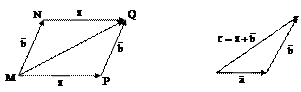
 .
. ,
, .
. .
.
 .
.