Нейронные сети (NN - Neural Networks) широко используются для решения разнообразных задач. Среди развивающихся областей применения NN - обработка аналоговых и цифровых сигналов, синтез и идентификация электронных цепей и систем. Основы теории и технологии применения NN широко представлены в пакете MATLAB. В этой связи особо следует отметить последнюю версию пакета - MATLAB 6.1, где впервые представлен GUI (Graphical User Interface - графический интерфейс пользователя) для тулбокса NNT. Примерами применения технологии нейронных сетей для цифровой обработки сигналов являются: фильтрация, оценка параметров, детектирование, идентификация систем, распознавание образов, реконструкция сигналов, анализ временных рядов и сжатие. Упомянутые виды обработки применимы к разнообразным видам сигналов: звуковым, видео, речевым, изображения, передачи сообщений, геофизическим, локационным, медицинских измерений (кардиограммы, энцефаллограммы, пульс) и другим.
Обработка сигналов в технологиях NN выполняется с помощью либо NN без памяти, либо NN c памятью. И в том и другом случаях ключевым элементом является NN без памяти. Подобная роль определяется тем обстоятельством, что при использовании нейронов с определёнными функциями активации (передаточными характеристиками) NN является универсальным аппроксиматором. Последнее означает, что в заданном диапазоне изменения входных переменных NN может с заданной точностью воспроизводить (моделировать) произвольную непрерывную функцию этих переменных.
Графический интерфейс пользователя NNTool позволяет выбирать структуры NN из обширного перечня и предоставляет множество алгоритмов обучения для каждого типа сети.
NN Tool пакета MATLAB, выполнять следующие действия при обработке данных:
|
|
- назначение графических управляющих элементов;
- подготовка данных;
- создание нейронной сети;
- обучение сети;
- прогон сети и др.
| КП – 2068280 – 080801– 12 - 2011 | ||||||||||
| Изм. | Лист | № документа | Подпись | Дата | ||||||
| Разработал | Фролова А.Ю. | Проектная часть | Литера | Лист | Листов | |||||
| Проверила | У | |||||||||
| Консультант | ТГТУ,0908 | |||||||||
| Утвердил | ||||||||||
3.Проектная часть
3.1 Применение сети обобщённой регрессии для решения задачи аппроксимации функции.
Демонстрационный пример demogrn1 в среде ПС MATLAB 6 иллюстрирует применение сети GRNN для решения задачи аппроксимации функции.
Приложение использует команду NEWGRNN для создания сети обобщённой регрессии, которая аппроксимирует функцию, заданную с помощью определенных точек;
|
Рис.1 Интерфейс пользователя
На рисунке 2 показан процесс формирования функции, которую мы хотим получить в результате аппроксимации, заданной обучающим множеством из 8 точек.
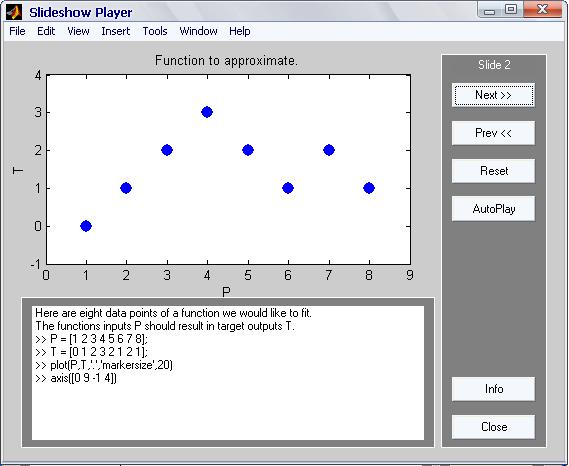
Рисунок 2.
Для того чтобы найти функцию, которая проходит через заданные на предыдущем слайде точки, необходимо применить сеть GRNN. На рисунке 3 представлены точки аппроксимации. Мы используем GRNN сеть для создания сети обобщённой регрессии. Мы используем параметр SPREAD на уровне чуть менее единицы. Расстояние между входными значениями, по сути, даёт функцию, которая подбирает значения максимально близкие к требуемым. Меньший разброс даст нам более точные результаты, но при этом мы потеряем плавность графика функции.
|
|
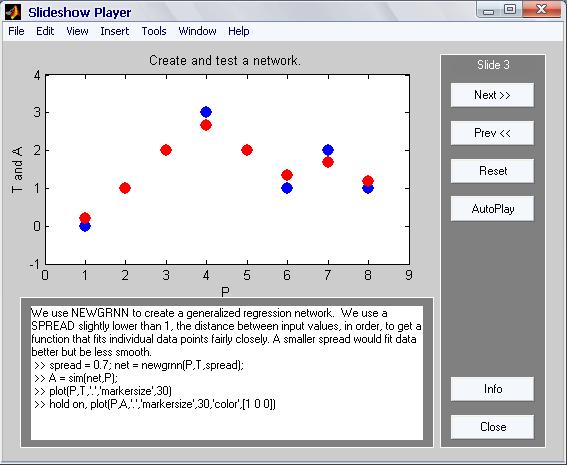
Рисунок 3.
После нажатия кнопки <next> переходим к следующему слайду (рис.4), на котором определяется новая точка ввода, аппроксимируемой функции (P=3.5)
Идея аппроксимации заключается в том, что при задании вектора входа каждый нейрон радиального базисного слоя выдаст значение в соответствии с тем, как близок вектор входа к вектору весов каждого нейрона.
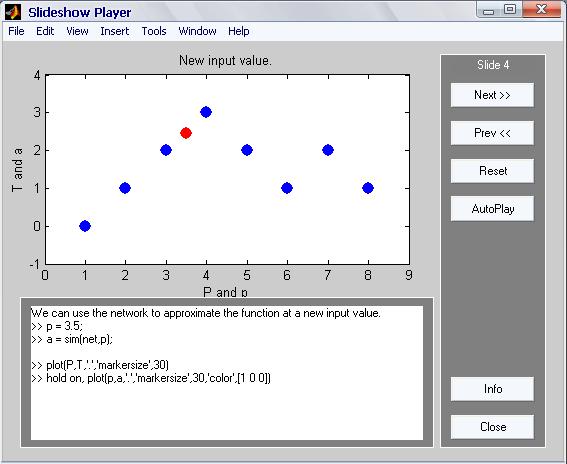
Рисунок 4.
На следующем слайде (рис.5) представлен отклик сети, симулированной в среде MATLAB. Отклик сети реализован по множеству данных, отражающих функцию, которую они представляют.
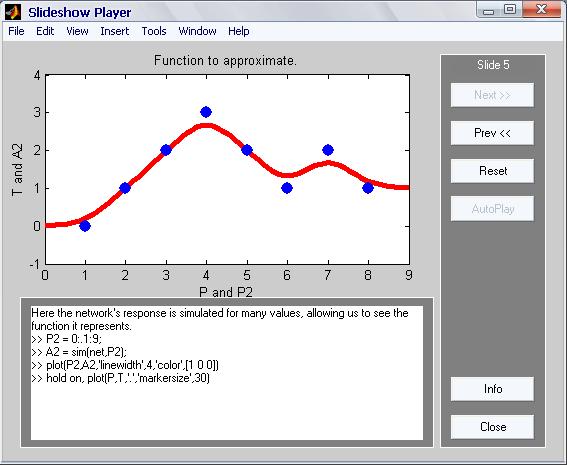
Рисунок 5.
Сформированная сеть GRNN использует всего 8 нейронов в скрытом слое и весьма успешно решает задачу аппроксимации и экстраполяции нелинейной зависимости, восстанавливаемой по экспериментальным точкам.
Итак, сеть GRNN использует, как и радиальная сеть, восемь нейронов.
Недостаток заключается в том, что погрешности ненулевые в отличие от радиальных сетей с нулевой ошибкой.
Достоинство в том, что скорость обучения очень высокая, так как обучение сводится только к присвоению значений весов.