Способы задания автоматов

Лекция 3.

Конечные детерминированные автоматы

Понятие конечного детерминированного автомата

Автоматы можно рассматривать как механизмы, состоящие из:

• блока управления, который может пребывать в различных состояниях (S внутренний алфавит);
• входного канала;
• выходного канала.

Входной канал считывает входные сигналы (Х) из внешней среды. Выходной канал выдает выходные сигналы (Y) во внешнюю среду. Работа автомата протекает в дискретные такты времени t =1,2,3,…. По команде 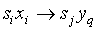в некотором такте времени 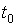блок управления установлен в состоянии 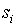и входной канал воспринимает 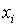, тогда в этом же такте 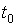в выходной канал выдается символ 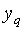, а к следующему такту 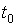+1 блок управления перейдет в состояние .

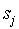Определение. К.Д.А. называется система 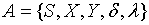, где 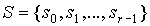- алфавит состояний, 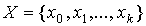– входной алфавит, 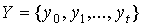– выходной алфавит. Множества S, X, Y – конечные.

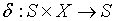– функция переходов,

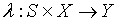– функция выходов.

Если в автомате выделено одно состояние, называемое начальным (обычно 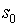), то автомат называется инициальным.

Способы задания автоматов

1. Таблица переходов–выходов.

S \ X		…		…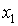
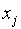
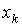
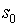
M
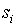
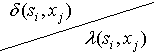
M

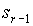
1. С помощью орграфов. Вершины граф означают состояния, а дуги – переходы между ними. Из каждой вершина исходит k дуг. Из вершины 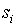проводится дуга в вершину 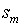в том и только в том случае, когда 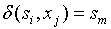для некоторого .
   
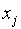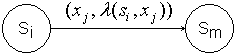
   Этой дуге приписывается пометка :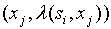

Начальное состояние в инициальном автомате помечается символом 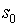. Описанный таким образом орграф с пометками называется диаграммой Мура.

1. С помощью канонических уравнений:

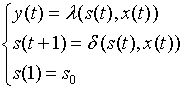
в момент t =1 автомат находится в начальном состоянии 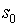. В каждый момент t =1,2,3,… дискретного времени автомат, находясь в некотором состоянии s (t) из множества S, под действием входного сигнала 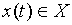выдает выходной сигнал 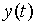из множества Y, согласно функции выходов l, а затем меняет свое состояние на s (t +1) согласно функции переходов d.

Для определения множества состояний автомата необходимо уяснить содержательный смысл и назначение понятия состояния.

После преобразования входного сигнала 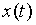в выходной 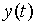его значение к следующему такту времени теряется. Иначе говоря, в любой тактовый момент t в устройстве нет информации о сигналах в предыдущие моменты, то есть о значениях 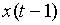, , 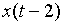,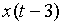…. Поэтому, если при вычислении значения функции переходов и выходов по формуле необходима информация об этих тактовых моментах, то ее нужно каким-либо образом "запомнить". В этом и состоит содержательное назначение состояний. Состояния – это вспомогательные объекты, которые подбираются таким образом, чтобы в совокупности с входным значением 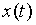однозначно определить выходное значение 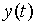. Обычно состояния кодируют ту информацию, которая поступила до момента t.

Пример. Построить таблицу переходов–выходов К.Д.А, реализующего функцию:

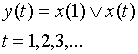
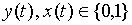
Чтобы на любом, отличном от первого, такте иметь информацию о 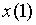, введем два следующих состояния:

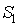={"на первом такте поступил 0"};

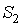={"на первом такте поступила 1"}.

И 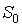–начальное состояние.

Построим таблицу переходов–выходов:

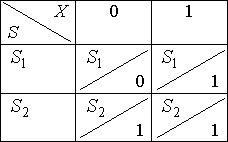
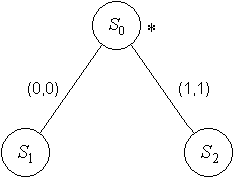
Для 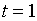нарисуем диаграмму Мура:

И дополним таблицу переходов–выходов: