Методические указания и контрольные задания
Для студентов – заочников по курсу
«Электротехника и электроника »
Контрольная работа №1
Тверь
| ОДОБРЕНА Цикловой /предметной/ комиссией «__»______________2014 г. Протокол № ___ Председатель цикловой /предметной/ комиссии ___________ В.А. Савельев | Методические указания и варианты заданий составлены в соответствии с рабочими программами по специальностям: 15.02.08 «Технология машиностроения», 22.02.06 «Сварочное производство», 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта». |
Разработчик: Баранов В.В., преподаватель
Рецензенты:
Бычкова Т.Г., преподаватель ГБОУ СПО «Тверской колледж имени А.Н.Коняева»
Никифорова Л.Н., преподаватель ГБОУ СПО «Тверской технологический колледж»
Введение
Весь курс «Электротехника и электроника» состоит из двух разделов: «Электротехника» и «Электроника». Данные методические указания разработаны для выполнения практических работ и решения задач студентами по разделу «Электротехника», так же возможно применение разработки при выполнение контрольных работ студентами заочной формы обучения.
Контрольные работы выполняются самостоятельно и отправляются в колледж в установленные сроки.
Изучение дисциплины завершается экзаменом (зачетом), к которому допускаются только студенты, выполнившие контрольную работу на положительную оценку.
При выполнении контрольных работ необходимо соблюдать следующие основные требования:
- работы выполняются на листах формата А4 печатным шрифтом, допускается выполнение в тетради; четко и аккуратно, с достаточными интервалами между строчками;
- при решение задач необходимо приводить используемые формулы и законы с расшифровкой символов;
- обязателен список используемой литературы и интернет источников;
- схемы и чертежи выполняются с помощью компьютера или карандашом;
- тексты условий задач переписываются обязательно;
- рекомендуется сначала решить задачу в общем виде, а затем, после подстановки данных числовых значений вычислить результат.
Содержание контрольной работы определяется преподавателем и может содержать решение задач и ответы на вопросы задания.
Литература
Основные источники:
- Немцов М.В. Электротехника и электроника: учебник для студ. образоват. учреждений сред. проф. образования. -М: Издательский центр «Академия», 2013
- Сиднеев Ю.Г. Электротехника с основами электроники: учебное пособие / Ростов н/Д: «Феникс», 2013
Дополнительные источники:
1. Данилов И.А., Иванов П.М. Общая электротехника с основами электроники: Учебное пособие для студ. неэлектротехн. спец. средних специальных учебных заведений. –М.: Высшая школа, 2005
2. Контрольные материалы по электротехнике и электронике: учебное пособие для учреждений среднего проф. образования.- М.: Издательский центр «Академия», 2011
Интернет-источники:
- Министерство образования тверской области: https://www.edu-tver.ru/
- https://electrono.ru /
- https://bourabai.kz
- https://elektrop2.ucoz.org
- https://elektro-tex.ru/
Пример 1.
Задача по теме 1.2 Электрические цепи постоянного тока (Л1 § 2.1-2.9; Л2 § 2.1-2.14):
Задача 1. Для схемы, изображенной на рис.1.1, заданы величины всех сопротивлений резисторов (R5 = 4 Ом) и напряжение UАВ= 80 В. Определить токи в каждом сопротивлении и напряжения на каждом резисторе. Решение проверить с помощью закона Кирхгофа и баланса мощностей.
Рис.1.1
Решение:
1. Сначала найдем суммарные сопротивления частей схемы:
R2,3= R2· R3/R2+R3 = 10 ·15/10+15 = 6 Ом;
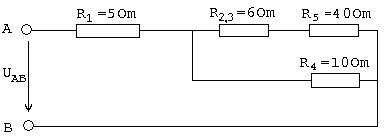
Рис.1.2
теперь вычислим:
R2,3,5= R2,3+ R5 = 6+4 = 10 Ом;
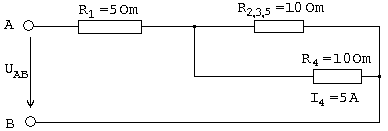
Рис.1.3
Общее сопротивление следующего разветвления:
R2,3,4,5 = R2,3,5·R4/ R2,3,5+R4 = 10·10/ 10 +10 = 5 Ом.
Рис.1.4
Эквивалентное сопротивление цепи:
RAB = R1+ R2,3,4,5 = 5+ 5= 10 Ом.
Рис.1.5
2. Обозначаем стрелками токи, проходящие через каждое сопротивление (см. рис. 1.1). Общий ток цепи:
I =I1 = UAB/ RAB = 80/ 10 = 8 A.
Напряжение на первом резисторе:
U1 = I1·R1 = 8·5 = 40 B.
Напряжения ветвей:
U4 = U2,3,5 = UAB - U1; U4 = U2,3,5 = 80 – 40 = 40 В.
Токи разветвления:
I4 = U4/ R4 = 40/ 10 = 4 A.
По первому закону Кирхгофа:
I = I4+I5; I5= I – I4 = 8 – 4= 4 А.
U5 = I5·R5 = 4·4 = 16 B.
Напряжения ветвей:
U2 = U3 = U2,3,5 – U5 ; U2 = U3 = 40 – 16 = 24 В.
I2 = U2/ R2 = 24/15 = 1,6 A;
I3 = U3/ R3 = 24/10 = 2,4 A.
3.Проверяем соблюдение первого закона Кирхгофа:
I1 = I2+I3+I4; 8 = 1,6 +2,4 +4
Проверяем правильность решения задачи с помощью баланса мощностей:
PAB = P1+P2+P3+P4+P5
или
UAB·I1 = I21R1+I22R2+I23R3+I24 R4+I25R5;
80·8 = 82·5+1,62·15+2,42·10+42·10+42·4;
640= 320+38,4+57,6+160+64.
Таким образом, задача решена верно.
Ответ: RAB =10 Ом; I =8 A.
Задачи по теме 1.4 Однофазные электрические цепи переменного тока (Л1 § 4.1-4.15; Л2§ 4.1-4.11):
Задача 2. Активное сопротивление катушки RК = 6 Ом, индуктивное XL = 10 Ом. Последовательно с катушкой включено активное сопротивление R = 2 Ом и конденсатор сопротивлением XC = 4 Ом (рис.2.а). К цепи приложено напряжение U = 50 В (действующее значение). Определить: полное сопротивление цепи; силу тока; коэффициент мощности; активную, реактивную и полную мощности; напряжения на каждом сопротивлении. Начертить в масштабе векторную диаграмму цепи.
Решение:
1. Определяем полное сопротивление цепи:
Z =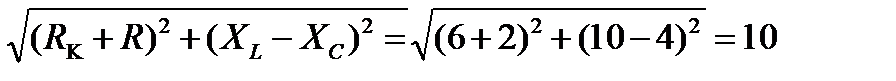 
Ом. 
2. Определяем силу тока в цепи:
I= U/z = 50/10 = 5 A.
3. Определяем коэффициент мощность цепи:
Sin φ = (ΧL-XC)/z = (10-4)/10 = 0,6;
по таблицам Брадиса находим φ = 36 
50´. Угол сдвига фаз φ находим по синусу во избежании потери знака угла (косинус является четной функцией).
4. Определяем активную мощность цепи:
P = I2· (RK+R) = 52· (6+2) = 200 Вт
или
P = U·I·cоsφ = 50·5·0¸8 = 200 (Вт).
Здесь cоs φ = (RK+R)/z = (6+2)/10 = 0,8.
5. Определяем реактивную мощность цепи:
Q = I2· (XL- X ̀C) = 52· (10- 4) = 150 вар
или
Q = U·I· sinφ = 50·5·0¸6 = 150 вар.
6. Определяем полную мощность цепи:
S = 
В·А
или
S = U·I = 50·5 = 250 В·А.
7. Определяем падения напряжения на сопротивлениях цепи:
URк = I·Rк =5·6 = 30 B;
UL = I·XL = 5·10 = 50 B;
UR = I·R = 5·2 = 10 B;
UC = I·XC = 5·4 = 20 B.
8. Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: μI =5/5=1,0 А/см (в 1 см – 1,0 А) и масштабом по напряжению μU =50/5=10 В/см (в 1 см – 10 В). Построение векторной диаграммы (рис. 2.б) начинаем с вектора тока, который откладываем по горизонтали в масштабе 
Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях URк и UR:
Из конца вектора UR откладываем в сторону опережения вектора тока на 90º вектор падения напряжения UL на индуктивном сопротивлении длиной 
. Из конца вектора UL откладываем в сторону отставания от вектора тока на 90º вектор падения напряжения на конденсаторе UC длиной 
Геометрическая сумма векторов URк, UR, UL и UC равна полному напряжению U, приложенному к цепи.
Ответ: z = 10 Ом; I = 5 Ом; sin φ = 0,6; Р = 200 Вт; Q = 150 вар; S = 250 В·А;
URк = 30 В;, UL = 50 В; UR = 10 В; UC = 20 В.
Задача 3. Катушка с активным сопротивлением R1 = 6 ОМ и индуктивным XL = 8 Ом соединена параллельно с конденсатором, емкостное сопротивление которого XC2 = 10 Ом (см. рис. 3.а). Определить: токи в ветвях и в неразветвленной части цепи; активные и реактивные мощности ветвей и в неразветвленной части цепи; активные и реактивные мощности ветвей и всей цепи; полную мощность цепи; углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму цепи. К цепи приложено напряжение U = 100 В.
Решение. 1. Определяем токи в ветвях:
I1 = 
= 
= 10 А;
I2 = U/X C2 = 100/10 = 10 А.
2. Углы сдвига фаз в ветвях находим по синусам углов во избежание потери знака угла:
sinφ1 = 
следовательно: φ1 = 53˚10.́
Так, как φ1 >0, то напряжение опережает ток;
sіnφ2 = -XC2/z2 = -10/10 = -1,0; φ2 =-90º, т.е. напряжение отстает от тока, так как φ2 <0.
По таблицам Брадиса находим cosφ1 = cos 53º10' = 0,6; cos φ2 = 0.
3.Определяем активные составляющие токов в ветвях:
Iа1 = I1·cos φ1 = 10·0¸6 = 6 A;
Ip1 = I1· sin φ1 = 10·0,8 = 8 A;
Ia2 = 0; Ip2 =10(-1¸0) = -10 A.
4. Определяем ток в неразветвленной части цепи:
I = 
5. Определяем коэффициент мощности всей цепи:
cos φ = 
6. Определяем активные и реактивные мощности ветвей и всей цепи:
P1 =U·I1·cosφ1 = 100·10·0,6 = 600 Bт;
P2 = 0; P = P1+P2 = 600 Вт;
Q1 = U·I1· sin φ1 = 100·10·0,8 = 800 вар;
Q2 = U·I·sin φ2 = 100·10(-1¸0) = -1000 вар
Q = Q1+Q2 = 800+(-1000) = -200 вар.
Внимание! Реактивная мощность ветви с емкостью отрицательная, так как φ2<0.
7. Определяем полную мощность цепи:
S = 
B·A.
Ток в неразветвленной части цепи можно определить значительно проще, без разложения токов на составляющие, зная полную мощность цепи и напряжение:
I = S/U = 633/100 = 6,33 A.
8. Для построения векторной диаграммы задаемся масштабом по току: μI =10/4=2,5 А/см (в 1 см – 2,5 А) и масштабом по напряжению: μU =100/4=25 В/см (в 1 см – 25 В).
Построение начинаем с вектора напряжения U (рис. 3.б). Под углом φ1 к нему (в сторону отставания) откладываем в масштабе вектор тока I1 , под углом φ2 (в сторону опережения) - вектор тока I2. Геометрическая сумма этих токов равна току в неразветвленной части цепи. На диаграмме показаны также проекции векторов токов на вектор напряжения (активная составляющая Iа1) и вектор, перпендикулярный ему (реактивные составляющие Ip1 и Ip2). При отсутствии конденсатора реактивная мощность первой ветви не компенсировалась и ток в цепи увеличивается до I = I1 = 10 A.
Ответ: I1 = 10 A; I2 = 10 A; I = 6,33 A; P = 600 B; Q =-200 вар;
S = 633 B·A; φ1 = 53º10'; φ2 = -90º.
Задачи по теме 1.6. Трехфазные электрические цепи (Л1 § 6.1-6.5; Л2 § 5.1-5.4).
Задача 4. В трехфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу А – конденсатор с емкостным сопротивлением XA = 10 Ом; в фазу В – активное сопротивление RB = 8Ом и индуктивное XВ = 6 Ом, в фазу С – активное сопротивление RС = 5 Ом. Линейное напряжение сети Uном = 380 В. Определить фазные токи, начертить в масштабе векторную диаграмму цепи и найти графически ток в нулевом проводе. Схема цепи рис. 4.а.
Решение:
1. Определяем фазные напряжения установки:
UA = UB = UC = Uном / 
= 380/ 
= 220 В.
2. Находим фазные токи:
IA = UA/ xА = 220/10 = 22 (А); IВ = UВ/ zB = 220/10 = 22 А.
Здесь zB = 
= 10 Ом;
IC = UC/ RC = 220/55 = 44 A.
Для построения векторной диаграммы выбираем масштабы по току: μI =10/1=10 А/см (1 см – 10 А) и по напряжению: μU =100/1=100 В/см (1 см – 100 В). Построение диаграммы начинаем с векторов фазных напряжений UA, UВ и UC, располагая их под углом 120º друг относительно друга (рис.4.б). Ток IA опережает напряжение UA на угол 90º; ток IВ отстает от напряжения UB на угол φВ, который определяется из выражения:
cosφВ = 
φВ = 36º50´.
Ток IC совпадает с напряжением UC. Ток в нулевом проводе равен геометрической сумме трех фазных токов. Измеряя длину вектора тока I0, которая оказалась равной 6,8 см; находим ток I0 = μI ·6,8 =10 А/см·6,8 см =
68 А.
Задача 5. В трехфазную сеть включили треугольником несимметричную нагрузку (рис.5.а): в фазу АВ – конденсатор с емкостным сопротивлением XAB = 10 Ом; в фазу ВС – катушку с активным сопротивлением RBC = 4 Ом и индуктивным XBC = 3 Ом; в фазу СА – активное сопротивление RCА = 10 Ом. Линейное напряжение сети Uном = 220 В. Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовые значения линейных токов.
Решение:
1. Определяем фазные токи и углы сдвига фаз:
IAB = Uном/ХАВ = 220/10 = 22 А; угол φAB = -90º;
IBС= Uном/ZBC = Uном/ 
;
cosφВС = RBC/ ZBC = 4/5 = 0,8; где ZBC = 
(Ом).
Отсюда угол φВС = 36º50´.
IСA = Uном/ RCА = 220/10 = 22 А; φСА = 0.
Для построения векторной диаграммы выбираем масштаб по току: μI =44/4,4 =10 А/см (1 см – 10 А), по напряжению μU =220/2,75=80 В/см (1 см - 80 В). Затем в принятом масштабе откладываем векторы фазных (они же линейные) напряжений UАВ, UВС, UСА под углом 120º друг относительно друга (рис.5.б). Под углом φАВ =-90º к вектору напряжения UАВ откладываем вектор тока IAB; в фазе ВС вектор тока IBС должен отставать от вектора напряжения UВС на угол φВС = 36º50´, а в фазе СА вектор тока IСA совпадает с вектором напряжения UСА. Затем строим векторы линейных токов на основании известных
уравнений:
IA= IAB- IСA= IAB+ (- IСA);
IB= IBС+ (- IAB);
IС = IСA+ (- IBС).
Измеряя длины векторов линейных токов (Li -см) и пользуясь принятым масштабом, находим значения линейных токов:
IA = μI · LА = 11 А;
IB = μI · LВ = 57 А;
IС = μI · LС = 47 А.
Ответ: IAB = 22 А; IBС = 44 А; IСA = 22 А; IA =11 А; IB = 57 А; IС = 47 А;
φAB = -90º; φВС = 36º50´; φСА = 0; IA = 11 А; IB = 57 А; IС = 47 А.
Задания для контрольной работы
Задача 1. Расчет электрических цепей с использованием законов Кирхгофа.
Резисторы заданного сопротивления (R 1…) соединены по схеме рис.6 и подключены к источнику постоянного напряжения U (тока I). Индекс тока или напряжения совпадает с индексом резистора по которому проходит этот ток или действует напряжение. Например: через резистор R3 проходит ток I3 и на нем действует напряжение U3 Определить общее сопротивление, ток в цепи I (напряжения U приложенное к цепи), силы тока и напряжения на каждом резисторе. Данные своего варианта принять по табл.1 и рис.6.
Указание: смотреть решение типовой задачи №1.
Табл.1
| Номер варианта | Схемы на рис.2 | Напряжение U, В | Сила тока I,А | Сопротивления резисторов,Ом | |||||
| R 1 | R 2 | R 3 | R 4 | R 5 | R 6 | ||||
| А | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| Б | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| В | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| Г | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - |
Схема А Схема Б
Схема В Схема Г
Рис.6 Схемы соединения резисторов
Задача 2. Расчет цепи переменного тока с последовательным соединением элементов.
Цепь переменного тока рис.7 содержит различные элементы (резисторы, индуктивности, емкости), включенные последовательно. Начертить схему цепи и определить следующие величины, относящиеся к данной цепи, если они не заданы в табл. 2: полное сопротивление z; напряжение U, приложенное к цепи; ток I; угол сдвига фаз (по величине и знаку); активную P, реактивную Q и полную S мощность цепи. Начертить в масштабе векторную диаграмму цепи и пояснить ее построение. Напряжение, приложенное к цепи, считать неизменным. Данные своего варианта принять по табл.2 и рис.7.
Примечание: индексы буквенных обозначений следует понимать так: QL1 – реактивная мощность в первом индуктивном сопротивлении, QC1 - то же, но в емкостном сопротивлении, PR1 – активная мощность в первом активном сопротивлении, UR1, UL1, UC1 – падения напряжения соответственно в первом активном, индуктивном, емкостном сопротивлениях.
Указание: смотреть решение типовой задачи №2.
Рис.7 Схема последовательного соединения резисторов
Рис.8Схема цепи переменного тока с двумя параллельными ветвями
Табл.2
| Номер варианта | R1 Ом | R2 Ом | XL1 Ом | XL2 Ом | XC1 Ом | XC2 Ом | Дополнительный параметр |
| - | - | U = 40 В | |||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | I = 5 А | |||||
| - | - | ||||||
| - | - | ||||||
| - | |||||||
| - | - | ||||||
| - | - | U = 90 В | |||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | |||||||
| - | I = 6 А | ||||||
| - | |||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | U = 120 В | |||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | I = 4 А | |||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - |
Задача 3. Расчет цепи переменного тока с параллельными ветвями.
Цепь переменного тока рис.8 содержит различные элементы (резисторы, индуктивности, емкости), расположенных на двух параллельных ветвях. Начертить схему цепи и определить следующие величины, относящиеся к данной цепи: токи в ветвях и в неразветвленной части цепи; активные и реактивные мощности ветвей и в неразветвленной части цепи; активные и реактивные мощности ветвей и всей цепи; полную мощность цепи; углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму цепи. К цепи приложено напряжение U. Данные своего варианта принять по табл.3 и рис.8.
Указание: смотреть решение типовой задачи №3.
Табл.3
| Номер варианта | R1 Ом | R2 Ом | XL1 Ом | XL2 Ом | XC1 Ом | XC2 Ом | Напряжение U, В |
| - | |||||||
| - | |||||||
| - | |||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | |||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
| - |
Задача 4. Расчет четырехпроводной трехфазной цепи с включенной звездой нагрузкой.
В трехфазную четырехпроводную сеть с линейным напряжением U ном включили звездой разные по характеру сопротивления (рис.9). Определить линейные токи и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовое значение тока в нулевом проводе. Данные своего варианта принять по табл.4 и рис.9.
Указание: смотреть решение типовой задачи №4.
Табл.4
| Номер варианта | RА Ом | RВ Ом | RС Ом | XА1 Ом | XВ1 Ом | XC1 Ом | XА2 Ом | XВ2 Ом | XC2 Ом | Напряжение Uном, В |
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | - | ||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | - | ||||||
| - | - | - | ||||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | ||||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | ||||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - | - | ||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | - |
Задача 5. Расчет трехпроводной трехфазной цепи с включенной треугольником нагрузкой.
В трехфазную трехпроводную сеть с линейным напряжением U ном включили треугольником разные по характеру сопротивления (рис.10). Определить фазные токи и начертить в масштабе векторную диаграмму цепи. Из векторной диаграммы определить числовые значения линейных токов. Данные своего варианта принять по табл.5 и рис.10.
Указание: смотреть решение типовой задачи №5.
Табл.5
| Номер варианта | RАВ Ом | RВС Ом | RСА Ом | XАВ1 Ом | X ВС1 Ом | XСА1 Ом | XАВ2 Ом | X ВС 2 Ом | XСА2 Ом | Напряжение Uном, В | ||||
| - | - | - | - | |||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | - | ||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | - | ||||||||||
| - | - | - | ||||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | |||||||||||
| - | - | - | ||||||||||||
| - | - | - | - | |||||||||||
| - | - | - | - | |||||||||||
-
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-29 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |