Методические советы по выполнению задания

Задачи 1–10 по теме «Статистические ряды распределения и их характеристики».

Ряд распределения – это ряд чисел, в котором значение изучаемого признака (варианты), расположены в определенном порядке: либо в порядке возрастания, либо убывания. Наряду с вариантами ряд распределения включает и частоты – величины, показывающие сколько раз каждая варианта встречается в данной совокупности. Сумма частот равна объему совокупности. Таким образом, ряд распределения состоит из вариант (х) и частот (т).

В зависимости от прерывности или непрерывности варьирующего признака ряды распределения удобно представлять в виде двух разновидностей: дискретного и вариационного (интервального). Дискретный ряд представляет собой ряд прерывных чисел. Например, распределение семей по числу членов (табл. I). При непрерывной вариации распределение признака называется интервальным. Частоты относятся ко всему интервалу. Примером интервального ряда может служить распределение совхозов области по проценту выполнения плана (табл. II).

Табл. I Табл. II

Распределение семей по числу членов		Распределение 365 совхозов по проценту выполнения плана
Число членов	Число семей (частоты)	Накопленные частоты	Процент выполнения плана	Число совхозов (частоты)	Накопленные частоты
			95–100 100–105 105–110 110–115 115–120 120–125 125–130 130 и выше
Итого			Итого

В зависимости от вида ряда распределения по разному можно изобразить их графически. Если ряд дискретный – строится полигон распределения. Величина признака откладывается на оси абсцисс, частоты – на оси ординат. Вершины ординат соединяются прямыми линиями. Гистограмма распределения отличается о полигона тем, что на оси абсцисс берутся не точки, а отрезки, изображающие интервал, т.е. гистограмма строится на основе вариационного (интервального) ряда. По накопленным частотам строится кумулятивная кривая (кумулята).

Для определения средней арифметической надо сложить все варианты и полученную сумму разделить на число единиц, входящих в совокупность (объем совокупности). Средняя арифметическая бывает простая и взвешенная. Простая средняя используется тогда, когда каждая варианта встречается лишь один раз. Если каждая варианта встречается несколько раз, то следует подсчитать частоты и умножить (взвесить) каждую варианту на соответствующую частоту.

Простая средняя арифметическая .

Средняя арифметическая взвешенная .

В наших примерах средняя рассчитывается по формуле взвешенной, для табл. I (чел.)

Для табл. II %.

При расчете средней арифметической для интервального ряда нужно сначала определить середины интервалов как полусуммы значений верхней и нижней границ интервала. При наличии интервалов, где «открыты» верхняя или нижняя граница, величину интервала определяют по последующему ил предыдущему интервалу.

Для характеристики рядов распределения кроме средней степенной применяются структурные средние: мода и медиана.

Мода – варианта, которая наиболее часто встречается в данной совокупности, т.е. варианта с наибольшей частотой.

Медиана – варианта, находящаяся в середине ряда распределения.

Мода для дискретного ряда определяется просто и соответствует варианте с наибольшей частотой. По данным табл. I мода равна 3, т.к. эта варианта встречается наибольшее число раз – 34. Значит, более всего в данной совокупности из 115 семей встречаются семьи с числом членов 3 человека. Для интервального ряда (с равными интервалами) мода определяется по следующей формуле:

где i – длина интервала; – частота модального, – домодального, – замодального интервалов; – начало модального интервала.

Медиану дискретного ряда определяют по накопленным частотам делением объема совокупности пополам: по табл. I – 115:2=57,5. Это соответствует медиане, равной 3.

Для интервального ряда медиану определяют по формуле:

где – накопленная частота интервала, предшествующего медианному; – локальная частота медианного интервала; – начало медианного интервала.

В нашем примере по данным табл. II получим:

Размах вариации – разность между наибольшей и наименьшей вариантой: . По данным дискретного ряда размах вариации равен 7=(8–1), по интервальному ряду 40=(135–95).

Среднее квадратическое отклонение – показатель вариации, измеряющий величину, на которую все варианты в среднем отклоняются от средней арифметической. Среднее квадратическое отклонение бывает простое и взвешенное и рассчитывается по формулам:

простое (невзвешенное) взвешенное

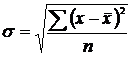
Квадрат среднего квадратического отклонения называется дисперсией, или средним квадратом отклонений. По данным табл. I, используя формулу взвешенного среднего квадратического отклонения, рассчитаем его величину:

(чел.)

Наряду с абсолютным показателем колеблемости признака – средним квадратическим отклонением, широко применяется и относительный показатель – коэффициент вариации, который показывает меру колеблемости признака относительно его среднего значения и измеряется в процентах. Расчет коэффициента вариации можно проследить по данным табл. I:

Задачи 11–27 относятся к теме «Выборочный метод» («Статистическая оценка характеристик генеральной совокупности»). Условия всех задач позволяют применять формулы для собственно случайной возвратной (повторной) выборки, поскольку относительный объем выборки предполагается небольшим (относительно объема генеральной совокупности). В задачах 11–17, 24 требуется дать точечную и интервальную оценки генеральной доли, а в задачах 18–23, 25–27 – точечные оценки генеральной средней и генерального среднего квадратического отклонения, а также интервальную оценку генеральной средней. Поскольку во всех задачах, кроме задач 26 и 27, абсолютный объем выборки все-таки достаточно большой, то распределение выборочной доли (в задачах 11–17, 24), а также выборочной средней (в задачах 18–23, 25) можно считать нормальным и использовать при решении задач таблицы функции Лапласа. В задачах 26 и 27 абсолютный объем выборки мал. В связи с этим, во-первых, необходимо при точечной оценке генерального среднего квадратического отклонения не забыть устранить смещенность выборочного среднего квадратического отклонения (путем умножения последнего на корректирующий множитель ). Во-вторых, необходимо использовать при интервальной оценке таблицу функции Стьюдента.

Рассмотрим типичные примеры по данной теме.

П р и м е р 1. Для оценки доли поврежденных клубней при механизированной уборке картофеля произведена случайная выборка объемом клубней. Из них поврежденных оказалось 40. Необходимо определить:

1) точечную оценку доли поврежденных клубней в генеральной совокупности;

2) доверительный интервал при доверительной вероятности 0,95;

3) вероятность того, что ошибка выборочной доли не превысит 0,03;

4) необходимый объем выборки, который с вероятностью 0,95 обеспечил бы ошибку выборочной доли не более чем 0,02.

Решение.

1) Рассчитываем выборочную долю: Она и будет точечной оценкой (состоятельной, несмещенной, эффективной) генеральной доли: .

2) Реально выборка в рассматриваемой ситуации производится, конечно, как безвозвратная. Однако поскольку объем выборки (количество отобранных клубней) заведомо мал относительно объема генеральной совокупности, то мы можем пренебречь различием формул для возвратной и безвозвратной выборок и использовать более простые формулы для возвратной выборки. Далее, выборочная доля имеет биномиальный закон распределения, однако при достаточно большом объеме выборки биномиальное распределение хорошо аппроксимируется нормальным. По заданной доверительной вероятности находим по таблице интегральной функции Лапласа соответствующее значение . Применяем формулу предельной ошибки выборочной доли:

Таким образом, доверительный интервал для генеральной доли р:

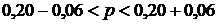или .

С вероятностью 0,95 в генеральной совокупности после механической уборки будет не мена 14%, но и не более 26% поврежденных клубней.

3) Имеем .

Отсюда .

По таблице интегральной функции Лапласа находим соответствующую доверительную вероятность .

5) Преобразовав соответствующим образом формулу предельной ошибки выборки, получаем:

Таким образом, сделав случайную выборку в количестве приблизительно полторы тысячи клубней и определив в ней долю поврежденных клубней, можно с практической достоверностью (вероятностью 95%) утверждать, что процент поврежденных клубней после механической уборки будет очень близким к проценту, установленному по выборке (отклонение в ту или другую сторону может составить не более 2%).

П р и м е р 2. Взвешивание 50 случайно отобранных поросят при рождении дало:

выборочная средняя г;

выборочная дисперсия г).

Необходимо определить:

1) точечные оценки средней и дисперсии в генеральной совокупности;

2) интервальную оценку средней при доверительной вероятности 0,95;

3) вероятность, что ошибка выборочной средней не превысит 20 г;

4) необходимый объем выборки, чтобы ошибка выборочной средней с вероятностью 0,99 не превышала 20 г.

Решение. Прежде всего отметим, что рассматриваемая в задаче выборка реально производится, конечно, как безвозвратная. Однако поскольку в качестве генеральной совокупности можно рассматривать всех рождающихся поросят данной породы при нормальных условиях содержания свиноматок, то объем выборки можно считать очень малым по сравнению с объемом генеральной совокупности. Поэтому в данной задаче можно использовать более простые соотношения для возвратной выборки.

1) В качестве точечной оценки генеральной средней необходимо положить выборочную среднюю, которая является состоятельной, несмещенной и эффективной оценкой генеральной средней:

г.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии. Несмещенной оценкой является величина . Однако при большом п отношение , как это имеет место и в нашей задаче. Поэтому в качестве точечной оценки генеральной дисперсии в нашей задаче можно принять величину .

2) Если объем выборки достаточно большой (практически начиная с ), то распределение выборочной средней , согласно центральной предельной теореме, независимо от характера генерального распределения приближается к нормальному распределению. Если само генеральное распределение нормально, то выборочная средняя будет иметь нормальное распределение при любом объеме выборки. По любой из этих двух причин распределение выборочной средней в нашей задаче можно считать нормальным. Далее, поскольку мы используем выборочную оценку неизвестной генеральной дисперсии , то статистика подчиняется закону распределения Стьюдента с степенями свободы. Однако при больших значениях параметра v 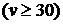распределение Стьюдента практически совпадает со стандартным нормальным распределением. Таким образом, в нашей задаче мы можем из равенства по таблице значений интегральной функции Лапласа определить . Применяя формулу предельной ошибки выборочной средней, находим

(г).

Таким образом, получаем доверительный интервал

3) Имеем .

Отсюда .

По таблице интегральной функции Лапласа находим соответствующую доверительную вероятность .

4) Из находим . Преобразовав соответствующим образом формулу предельной ошибки выборки, получаем

(голов).

П р и м е р 3. Для определения среднего веса бычков красной степной породы в возрасте 12 мес. при соблюдении требуемых условий содержания было взвешено 10 бычков, вес которых оказался равным (кг): 325; 337; 319; 330; 327; 328; 332; 320; 318; 334. Необходимо определить:

1) точечные оценки среднего веса бычков в генеральной совокупности, а также генеральной дисперсии и среднего квадратического отклонения;

2) доверительный интервал для генеральной средней с вероятностью 0,95;

3) вероятность, что ошибка выборочной средней не превысит 3 кг;

4) необходимый объем выборки, чтобы с вероятностью 0,95 гарантировать ошибку выборки не более 3 кг.

Решение. Прежде всего отметим, что в качестве генеральной совокупности в нашей задаче можно рассматривать всех бычков данной породы, которые достигли или будут достигать в будущем указанного возраста (при нормальных условиях содержания). Объем выборки, таким образом, ничтожно мал по сравнению с объемом генеральной совокупности, что позволяет применять формулы для возвратной выборки.

(кг).

Рассчитаем выборочную дисперсию:

Выборочная дисперсия является смещенной оценкой генеральной дисперсии. Несмещенной точечной оценкой является величина:

Соответственно, несмещенной точечной оценкой генерального среднего квадратического отклонения будет величина:

(кг).

2) Анализ биологических и производственных условий массового выращивания бычков дает основания полагать, что вес бычков в генеральной совокупности имеет нормальное распределение. Поэтому выборочная средняя, независимо от объема выборки, также будет иметь нормальный закон распределения, а статистика подчиняется закону распределения Стьюдента с степенями свободы. Обращаясь к таблице значений функции Стьюдента по данным и , находим .

Вычисляем предельную ошибку выборки:

(кг).

Доверительный интервал для генеральной средней:

или .

3) Имеем .

Отсюда ..

Обращаясь к таблице функции Стьюдента, по заданным и находим .

4) Преобразовав соответствующим образом формулу предельной ошибки выборки, получаем

. (*)

Однако из условия мы не можем определить , поскольку нам неизвестно . Поэтому воспользуемся схемой последовательной приближений. Определим сначала из таблицы функции Лапласа (по заданной вероятности ). Находим . Затем найдем п ₁, используя формулу (;): . Теперь обращаемся к таблице функции Стьюдента и по находим значение . Вычисляем . По и находим . Вычисляем . Поскольку , то необходимый объем выборки устанавливается (голов).