Отсев грубых погрешностей на примере
Для выборки, представленной в таблице 1.1 (n = 25), необходимо провести отсев грубых погрешностей.
1. Отсев грубых погрешностей методом максимального относительного отклонения:
а) вычисляем среднее значение выборки:
б) вычисляем среднеквадратичное отклонение:
в) определяем статистику для крайних (наибольшего или наименьшего) элементов выборки:
- для наибольшего элемента выборки 
- для наименьшего элемента выборки 
г) определяем табличное значение статистики (Приложение) при доверительной вероятности q = 0,95 или уровне значимости 0,05
д) сравниваем найденные значения статистики с табличным значением
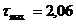
2,06 < 2,62 - наблюдение отсеивать нельзя
1,42 < 2,62 - наблюдение отсеивать нельзя
2 Отсев грубых погрешностей для выборок малых объемов. Возьмем выборку n=10 и представим ее в виде вариационного ряда (таблица 3.1).
Таблица 3.1 – Значения выборки
| № | ||||||||||
| xi | 0,15 | 0,34 | 0,99 | 1,11 | 1,57 | 2,23 | 2,34 | 2,34 | 2,48 | 4,15 |
По формуле 3.5 вычислим значение τ. Для этого необходимо вычислить
среднеквадратичное отклонение по формуле 3.2.
Данные необходимые для вычисления 
приведем в таблице 3.2.
Таблица 3.2 - Данные для вычисления
| № | xi | 
| 
|
| 0,15 | -1,62 | 2,624 | |
| 0,34 | -1,43 | 2,045 | |
| 0,99 | -0,78 | 0,608 | |
| 1,11 | -0,66 | 0,436 | |
| 1,57 | -0,2 | 0,04 | |
| 2,23 | 0,46 | 0,212 | |
| 2,34 | 0,57 | 0,325 | |
| 2,34 | 0,57 | 0,325 | |
| 2,48 | 0,71 | 0,504 | |
| 4,15 | 2,38 | 5,664 | |
| ∑ | 17,7 | 12,783 |
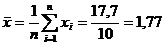
Определяем статистику для крайних (наибольшего или наименьшего) элементов выборки по формуле:
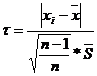
- для наибольшего элемента выборки 
|
|
- для наименьшего элемента выборки
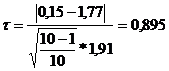
г) определяем табличное значение статистики (Приложение) при доверительной вероятности q = 0,95 или уровне значимости 0,05
д) сравниваем найденные значения статистики с табличным значением
1,315 < 2,29 - наблюдение отсеивать нельзя
0,895 < 2,29 - наблюдение отсеивать нельзя.
3 Отсев грубых погрешностей для выборок большого объема (использование таблиц распределения Стьюдента).
Для выборки, представленной в таблице 1.1 (n = 20), необходимо провести отсев грубых погрешностей с использованием таблиц распределения Стьюдента.
Определяем среднее значение для данной выборки, отклонение от среднего для каждого члена выборки и среднеквадратичное отклонение. Все результаты вычисления сведем в таблицу 3.3.
Таблица 3.3 - Данные для вычисления 
,
| № | 
| 
| 
| № |
|
|
|
| 9,81 | 5,734 | 32,879 | 6,72 | 2,644 | 6,991 | ||
| 2,34 | -1,736 | 3,0137 | 5,15 | 1,074 | 1,153 | ||
| 6,55 | 2,474 | 6,121 | 0,34 | -3,736 | 13,958 | ||
| 0,15 | -3,926 | 15,413 | 2,23 | -1,846 | 3,408 | ||
| 8,63 | 4,554 | 20,739 | 4,85 | 0,774 | 0,599 | ||
| 7,11 | 3,034 | 9,205 | 5,01 | 0,934 | 0,872 | ||
| 1,57 | -2,506 | 6,280 | 4,15 | 0,074 | 0,005 | ||
| 2,34 | -1,736 | 3,014 | 1,11 | -2,966 | 8,797 | ||
| 5,55 | 1,474 | 2,173 | 2,48 | -1,596 | 2,547 | ||
| 0,99 | -3,086 | 9,523 | 4,44 | 0,364 | 0,132 | ||
| ∑ | 81,52 | 146,824 |
Из таблицы 3.3 выберем наблюдения, имеющие наибольшее и наименьшее отклонения:
Вычисляем τ для 
по формуле (3.7).
По таблице (Приложение) находим процентные точки t -распределения Стьюдента для 5% и 0,1% и соответствующем объеме выборки (n =20).
|
|
t(0,1; 18) = 3,6105 t(5; 18) = 1,7341
Вычисляем соответствующие точки критического значения 
по формуле (3.8) и (3.9):
Полученные сравниваем с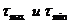 
и делаем соответствующие выводы.
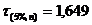
Тогда, для максимального значения выборки выполняется условие
1,6491<2,061<2,825 – решение об отсеве данного наблюдения принимается экспериментатором.
Для минимального значения выборки выполняется условие 1,412<1,6491 – наблюдение отсеивать не нужно.
Практическое занятие №4. Методики проверки гипотезы нормальности распределения.
Основные понятия и определения
При обработке экспериментальных данных в науке и технике обычно предполагают нормальный закон распределения случайных величин.
Свойства нормально распределенной случайной величины x:
- 
;
- плотность вероятности 
является непрерывной функцией;
- центр распределения случайной величины одновременно является центром симметрии;
- малые отклонения встречаются чаще больших (с большей вероятностью).
Наиболее полной характеристикой случайной величины является закон распределения вероятностей случайной величины, который связывает данное значение случайной величины с вероятностью появления его (т.е. этого значения) в опыте. Наиболее распространенным является закон распределения, получивший название нормального. В аналитическом виде этот закон выражается известным уравнением Гаусса:
, (4.1)
где 
- плотность вероятностей при данном значении х.
Графически это уравнение имеет вид колоколообразной кривой, которая симметрична относительно центра распределения, которым является Мх (максимум функции ) и концы которой уходят в ±¥, асимптотически приближаясь к горизонтальной оси х и не достигая ее.
|
|
При обработке экспериментальных данных если закон распределения генеральной совокупности, из которой взята наша выборка, неизвестен, то первое, что надо сделать - это проверить распределение в выборке на нормальность, т.е. соответствие закону нормального распределения.
Предположение о подчинении выборки на соответствие закону нормального распределения можно сделать:
1. По коэффициенту вариации (2.13).
Если коэффициент вариации превышает 33%, говорить о нормальности распределения данных выборки нельзя.
Предварительный анализ с помощью коэффициента вариации дает самую грубую оценку.
2. По коэффициентам эксцесса и ассиметрии (2.11 - 2.12).
Для нормально распределенной случайной величины коэффициенты эксцесса и асимметрии равны 0. Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что генеральная совокупность распределена по нормальному закону.
3. По несмещенным оценкам для показателей асимметрии и эксцесса.
Для этого необходимо определить несмещенные оценки для показателей асимметрии и эксцесса по формулам 4.2 и 4.3 соответственно:
(4.2)
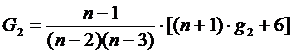(4.3)
Определяют среднеквадратические отклонения для показателей асимметрии и эксцесса по формулам 4.4 и 4.5 соответственно:
(4.4)
(4.5)
Проверяют условия:
(4.6)
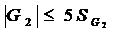(4.7)
Если условия выполняются, то гипотеза нормальности распределения принимается
4. Для не очень больших выборок (n <120) можно вычислить среднее абсолютное отклонение (САО):
, (4.8)
где n – объем выборки;
- среднее значение выборки.
Для выборки, имеющей приближенно нормальный закон распределения, должно выполняться условие:
(4.9)
5. Проверку гипотезы нормальности распределения для сравнительно широкого класса выборок (3< n <1000) можно выполнить с помощью метода, основанного на размахе варьирования R.
Подсчитывают отношение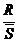 
, где R – размах варьирования (ширина интервала), 
- несмещенной оценки дисперсии теоретического распределения (2.6) и сопоставляют с критическими верхними и нижними границами этого отношения (Приложение).
Если данное отношение меньше нижней границы или больше верхней границы, то нормального распределения нет. Как правило это условие проверяется при 10%-ном уровне значимости.
6. Проверку гипотезы нормальности распределения можно провести по критерию χ2.
Для этого необходимо:
- разбить массив исходных данных на классы по формуле 1.1.
- определить середины классов x по формуле 1.4.
- подсчитать частоты для всех классов В (наблюдаемая абсолютная частота);
- вычислить для всех классов Вх и Вх2;
- определить 
по формулам:
(4.10)
(4.11)
- вычислить
(4.12)
- определить
(4.13)
- формируют с помощью таблицы (ординаты стандартной нормальной кривой) вектор столбец f(z);
н) вычисляют для всех классов f(z)k’, 
, 
, где Е= f(z)k' ожидаемая по стандартному нормальному распределению частота.
Если в каком-либо классе число наблюдений окажется меньше четырех, то его объединяют с соседним классом (классами) так, чтобы число наблюдений в таком объединенном классе оказалось большим или равным четырем.
о) вычисляют χ2 по формуле 
(4.14)
п) проверяют, используя таблицу (процентные точки распределения χ2) условие χ2< χ2(ν;p), где ν = nкл -1 -2; p=0,10
Проверка гипотезы нормальности распределения по различным методикам
Выборку представленную в таблице 4.1 проверим на подчинение нормальному закону распределения используя различные методики.
Таблица 4.1 – Таблица значений выборки (наблюдений)
| № значения выборки | Значения выборки (х) | № значения выборки | Значения выборки (х) |
Вычислим основные выборочные характеристики. Вычисления будем производить в табличной форме (таблица 4.2).
Таблица 4.2 – Данные для вычисления выборочных характеристик
| № |
|
|
| 
| 
|
| 10,05 | 101,00 | 1015,05 | 10201,00 | ||
| -11,95 | 142,80 | -1706,46 | 20391,84 | ||
| -15,95 | 254,40 | -4057,68 | 64719,36 | ||
| 4,05 | 16,04 | 64,96 | 257,28 | ||
| -7,95 | 63,20 | -502,44 | 3994,24 | ||
| -19,95 | 398,00 | -7940,1 | 158404,00 | ||
| -13,95 | 194,60 | -2714,67 | 37869,16 | ||
| 6,05 | 36,60 | 221,43 | 1339,56 | ||
| -5,95 | 35,40 | -210,63 | 1253,16 | ||
| -0,95 | 0,90 | -0,855 | 0,81 | ||
| 1,05 | 1,10 | 1,155 | 1,21 | ||
| 14,05 | 197,40 | 2773,47 | 38966,76 | ||
| 3,05 | 9,30 | 28,365 | 86,49 | ||
| 9,05 | 81,90 | 741,195 | 6707,61 | ||
| 17,05 | 290,70 | 4956,43 | 84506,49 | ||
| -9,95 | 99,00 | -985,05 | 9801,00 | ||
| 27,05 | 731,70 | 19792,48 | 535384,89 | ||
| -2,95 | 8,70 | -25,66 | 75,69 | ||
| -1,95 | 3,80 | -7,41 | 14,44 | ||
| 0,05 | 0,0025 | 0,000125 | 0,000006 | ||
| ∑ | 2666,54 | 11443,57 | 973974,99 |
1. По коэффициенту вариации.
Вычислим коэффициент вариации по формуле 2.13:
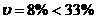. Следовательно выборка подчиняется нормальному закону распределения.
2. По коэффициентам эксцесса и ассиметрии.
Вычислим коэффициент асимметрии по формуле 2.12:
Так как g1 = 0,37 ≠ 0. Следовательно, некоторая асимметрия имеет место.
Вычислим коэффициент эксцесса по формуле 2.11:
Так как g2 = -0,26<0. Имеется небольшой эксцесс.
3. По несмещенным оценкам для показателей асимметрии и эксцесса.
Для этого необходимо определить несмещенные оценки для показателей асимметрии и эксцесса по формулам 4.2 и 4.3 соответственно:
Определим среднеквадратические отклонения для показателей асимметрии и эксцесса по формулам 4.4 и 4.5 соответственно:
Проверяем условия:
Условия выполняются, гипотеза нормальности распределения может быть принята.
4. По среднему абсолютному отклонению (САО)
Данные для вычисления САО приведены в таблице 4.3.
Таблица 4.3 - Данные для вычисления САО
| № |
|
| 
|
| № |
|
| 
|
|
| 10,05 | 10,05 | 101,00 | 1,05 | 1,05 | 1,10 | ||||
| -11,95 | 11,95 | 142,80 | 14,05 | 14,05 | 197,40 | ||||
| -15,95 | 15,95 | 254,40 | 3,05 | 3,05 | 9,30 | ||||
| 4,05 | 4,05 | 16,04 | 9,05 | 9,05 | 81,90 | ||||
| -7,95 | 7,95 | 63,20 | 17,05 | 17,05 | 290,70 | ||||
| -19,95 | 19,95 | 398,00 | -9,95 | 9,95 | 99,00 | ||||
| -13,95 | 13,95 | 194,60 | 27,05 | 27,05 | 731,70 | ||||
| 6,05 | 6,05 | 36,60 | -2,95 | 2,95 | 8,70 | ||||
| -5,95 | 5,95 | 35,40 | -1,95 | 1,95 | 3,80 | ||||
| -0,95 | 0,95 | 0,90 | 0,05 | 0,05 | 0,0025 | ||||
| Сумма | 2666,54 |
Вычислим среднее абсолютное отклонение (САО).
Проверяем условие 
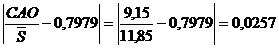
, условие выполняется, следовательно гипотеза нормальности распределения выборки принимается.
5. По размаху варьирования.
Вычислим отношение .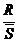
Критическая нижняя граница данного отношения при 10% уровне значимости равна 3,29
Критическая верхняя граница данного отношения при 10% уровне значимости равна 4,32
Сравниваем полученное значение отношения с критическими значениями верхней и нижней границ.
3,29<3,97< 4,32
Так как значение отношения больше нижней границы критического значения и меньше значения верхней границ, следовательно гипотеза нормальности распределения выборки по данному методу принимается.
6. По критерию χ2.
Проверку гипотезы нормальности распределения по критерию χ2 будем проводить для выборки представленной в таблице 4.1.
Разбиваем массив исходных данных (наблюдений) на классы по формуле 1.1.
Определим ширину класса по формуле (1.2). Результат вычисления округляем до ближайшего целого.
Определим середины классов x по формуле 1.4.
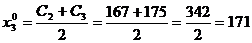
Подсчитаем частоты для всех классов В.
При этом значения хi попавшие на границу между (k-1) и k классами, будем относить к k -му классу.
Вычислим для всех классов Вх и Вх2. Расчеты представим в табличной форме (таблица 4.4)
Определим по формулам 4.10 - 4.11.
Вычислим 
и 
по формулам 4.12 – 4.13.
С помощью таблицы ординаты стандартной нормальной кривой сформируем вектор столбец f(z).
Вычислим для всех классов f(z)k, , и χ2 по формуле 4.14.
Проверяем, используя таблицу (процентные точки распределения χ2) условие χ2< χ2(ν;p), где ν = nкл -1 -2; p=0,10.
χ2(1;0,12)=2,706
χ2 = 0,184 0,184<2,706
Условие выполняется, гипотеза о том, что наблюдаемые частоты распределены нормально принимается на 10%-ном уровне.
Таблица 4.4 – Процедура вычисления критерия χ2
| № класса | Середины классов x | Частоты В | х2 | Вх | Вх2 |
|
| Ордината f(z) | f(z)k’ | Е |
|
|
|
| -16,4 | 1,47 | 0,1354 | 1,94 | 6,26 | 0,74 | 0,548 | 0,087 | ||||||
| -8,4 | 0,75 | 0,3011 | 4,32 | ||||||||||
| -0,4 | 0,04 | 0,3986 | 5,72 | 5,72 | 0,28 | 0,078 | 0,014 | ||||||
| 7,6 | 0,68 | 0,3166 | 4,54 | 4,54 | -0,54 | 0,292 | 0,064 | ||||||
| 15,6 | 1,40 | 0,1497 | 2,15 | 2,77 | 0,23 | 0,053 | 0,019 | ||||||
| 23,6 | 2,11 | 0,0431 | 0,62 | ||||||||||
| ∑ | 0,184 |