Формула парабол (Симпсона)

Постановка задачи численного интегрирования

Пусть требуется найти значение определенного интеграла:

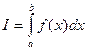
где f(х) — непрерывная на отрезке [ a; b ] функция. Если известна ее первообразная, то интеграл можно вычислить по формуле Ньютона—Лейбница:

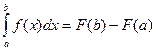
Здесь F(х) - одна из первообразных функций. Однако даже в тех случаях, когда первообразную удается явно найти в аналитической форме, не всегда удается довести до числового ответа значение определенного интеграла. К тому же, иногда подынтегральная функция задается таблицей или графиком или первообразная не выражается через элементарные функции в конечном виде. В таких случаях применяют различные методы приближенного (численного) интегрирования. Формулы, используемые для приближенного вычисления интегралов, называют квадратурными формулами.

Прием построения квадратурных формул состоит в том, что подынтегральная функция f(х) заменяется на отрезке [ a; b ] интерполяционным многочленом, т.е. f(x) = F_n(x) + R_n(x). Тогда 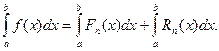Узлы интерполирования х_0, х₁, …, х_п принадлежат отрезку [ a; b ]. Оба интеграла существуют и тогда можно принять: 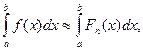а погрешность при этом будет равна .

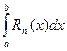Квадратурные формулы Ньютона-Котеса

Если выбрать в качестве интерполяционного многочлена F_n(x) интерполяционный многочлен Лагранжа L_n(x) c равноотстоящими узлами, то получают формулы численного интегрирования, называемые квадратурными формулами Ньютона – Котеса.

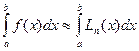. (1)

Подобный подход удобен тем, что он приводит к алгоритмам, легко реализуемым на компьютере и позволяющим получить результат с точностью, достаточной для широкого круга практических приложений. При этом предполагается, что отрезок [ a; b ] разбит на п равных частей точками .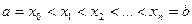

Подставляя в (1) вместо L_n(х) его представление, получим

=

= ,

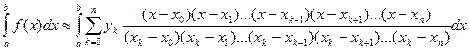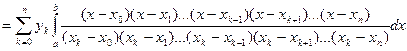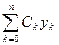где 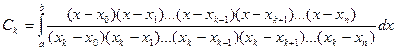- коэффициенты Котеса.

Эти коэффициенты не зависят от вида функции f(x),а только от узлов интерполирования.

Введя новую переменную 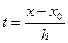, или x = x₀ + th, получим интерполяционный многочлен Лагранжа для равноотстоящих узлов:

.

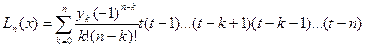Перейдем к переменной интегрирования t:

x = x₀ + th, dx = hdt, x=a → t=0, x=b → t=n и окончательно для коэффициентов Котеса получим выражение:

.

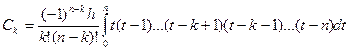Формулы прямоугольников

Отрезок [ a; b ] разбивается на n равных частей длины 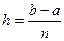и для точек деления x_{0 ,} x_{1 ,} х₂,… x_n вычисляются значения интегрируемой функции y=f(x). Считаем, что х₀=а, х_n=b. Площадь криволинейной трапеции заменяется суммарной площадью полученных прямоугольников.

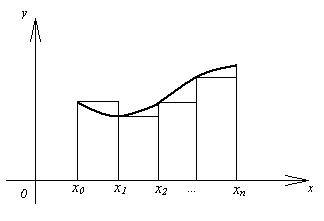
В этом случае для вычисления определенного интеграла получаем приближенное выражение (формула левых прямоугольников):

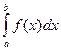≈ h(y₀ + y ₁ + … + y_{n- 1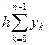} ) = (2)

Если за узел интерполирования на каждом частичном отрезке брать правый конец, то получим формулу правых прямоугольников:

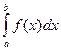≈ h(y₁ + y₂ + … + y_n) = 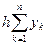(3)

Если за узел интерполирования на каждом частичном отрезке брать середину отрезка, то получим формулу средних прямоугольников:

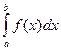≈ (4)

Вычисленное значение тем точнее, чем больше число n. Оценка погрешности при вычислении по формулам прямоугольников определяется выражением:

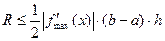, (5)

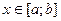где , а 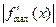- максимальная величина абсолютного значения первой производной во всем интервале интегрирования.

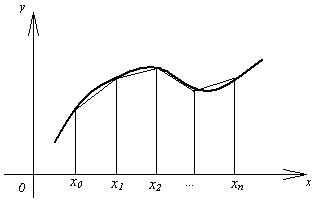
Формула трапеций

Данный метод приближенного вычисления интеграла отличается от методов прямоугольников тем, что площадь криволинейной трапеции заменяется суммарной площадью прямоугольных трапеций.

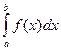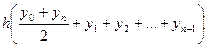≈ (6)

Оценка погрешности при вычислении по формуле трапеций определяется формулой

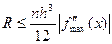(7)

Формула парабол (Симпсона)

Точность вычислений значительно возрастет, если на каждом частичном отрезке дугу кривой f(x) заменить дугой параболы. Отрезок 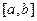разбивается на 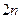равных частей точками: 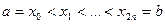, где

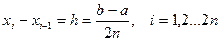. На участках 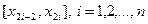функцию 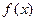заменяют на параболу, проходящую через точки 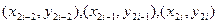и интегралом от этой параболы на участке 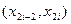заменяют интеграл от функции 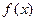на этом же участке, после чего все эти интегралы суммируют и результаты принимают за интеграл от 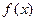по всему отрезку 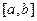. Вот ее окончательный вид:

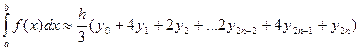. (8)

Оценка погрешности при вычислении интеграла по формуле парабол определяется по формуле:

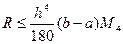, (9)

где 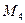- максимальное значение четвертой производной функции 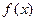на интервале .

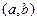На практике для оценки погрешности часто используют формулу практической оценки:

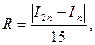(10)

где I_n – значение интеграла, вычисленного при разбиении п частей, I_2n – при разбиении на 2п частей.