Основные определения.
Определение 1. Пусть X и Y – произвольные множества. Будем говорить, что A – отображение, действующее из X в Y и записывать это так A: X ®Y, если имеется правило, с помощью которого каждому элементу 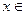 X ставится в соответствие единственный элемент
X ставится в соответствие единственный элемент 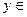 Y, обозначаемый A
Y, обозначаемый A 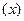 или A
или A 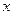 .
.
Элемент 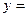 A
A 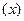 называют образом элемента
называют образом элемента 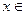 X при отображении A. Элемент
X при отображении A. Элемент 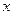 называют прообразом элемента
называют прообразом элемента 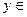 Y при отображении A.
Y при отображении A.
Если для каждого элемента 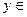 Y существует единственный прообраз
Y существует единственный прообраз 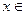 X, то отображение A называют взаимнооднозначным.
X, то отображение A называют взаимнооднозначным.
Пример 1. Каждой точке 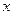 отрезка
отрезка 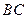 поставим в соответствие точку
поставим в соответствие точку 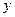 , являющуюся проекцией точки
, являющуюся проекцией точки 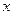 на прямую
на прямую 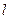 , параллельную отрезку
, параллельную отрезку 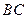 . Это отображение не является взаимнооднозначным, т.к. не всякая точка прямой
. Это отображение не является взаимнооднозначным, т.к. не всякая точка прямой  есть образ некоторой точки отрезка
есть образ некоторой точки отрезка  .
.
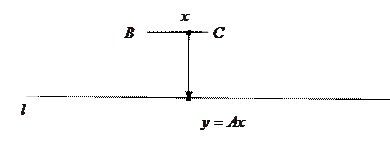
Пример 2. Пусть даны два параллельных отрезка 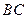 и
и 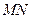 . Проведем прямые
. Проведем прямые 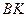 и
и 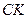 через точки
через точки 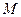 и
и 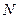 соответственно.
соответственно.
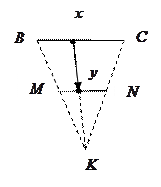 Каждой точке
Каждой точке 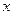 отрезка
отрезка 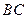 поставим в соответствие точку
поставим в соответствие точку 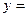 A
A 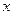 отрезка
отрезка 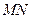 , являющуюся точкой пересечения отрезка
, являющуюся точкой пересечения отрезка 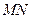 и отрезка, соединяющего точки
и отрезка, соединяющего точки 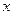 и
и 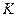 . Очевидно, это отображение является взаимнооднозначным.
. Очевидно, это отображение является взаимнооднозначным.
Определение 2. Пусть X и Y – линейные пространства над полем K. Отображение A: X ®Y пространства X в пространство Y называется линейным, если для любых векторов  X и для любых чисел
X и для любых чисел  K справедливо равенство
K справедливо равенство
A (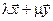 ) =
) =  A (
A ( ) +
) +  A (
A ( ).
).
Если 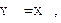 то такое линейное отображение будем называть линейным оператором, т.е.
то такое линейное отображение будем называть линейным оператором, т.е.
отображение A: X ®X будем называть линейным оператором, если для любых векторов  X и для любых чисел
X и для любых чисел  K справедливо равенствоA (
K справедливо равенствоA (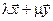 ) =
) =  A (
A ( ) +
) +  A (
A ( ).
).
Множество всех линейных отображений, действующих из X в Y, будем обозначать так: 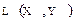 . Множество всех линейных операторов, действующих в пространстве X, будем обозначать через
. Множество всех линейных операторов, действующих в пространстве X, будем обозначать через 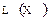 , т.е.
, т.е. 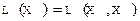 . Иногда вместо A (
. Иногда вместо A ( ) будем писать A
) будем писать A  .
.
Взаимнооднозначное линейное отображение будем называть изоморфизмом линейных пространств. Если существует изоморфизм линейных пространств A: X ®Y, то будем говорить, что пространство X изоморфно пространству Y и записывать это так: X 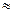 Y.
Y.
Задача 1. Докажите, что если A 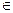 L (X), то A
L (X), то A 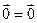 .
.
Пример 1. Отображение 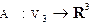 , сопоставляющее каждому вектору
, сопоставляющее каждому вектору 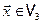
пространства свободных векторов в пространстве его столбец координат  в базисе
в базисе 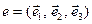 , т.е. такое, что,A
, т.е. такое, что,A 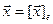 является линейным.
является линейным.
Действительно,A (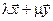 ) =
) = 
 A (
A ( ) +
) +  A (
A ( ) для любых
) для любых  X и для любых чисел
X и для любых чисел  R. Нетрудно доказать, что это изоморфизм линейных пространств.
R. Нетрудно доказать, что это изоморфизм линейных пространств.
Пример 2. Пусть X  (C),
(C), 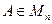 (C), – фиксированная матрица. Отображение
(C), – фиксированная матрица. Отображение
A: X ®X, заданное формулой A 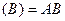 для любой матрицы
для любой матрицы 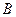 ÎX, является линейным оператором, т.к.
ÎX, является линейным оператором, т.к.
A  A
A 
 A
A  для любых чисел
для любых чисел  C и для любых матриц
C и для любых матриц  X
X  (C).
(C).
Докажите, что A - изоморфизм линейных пространств тогда и только тогда, когда матрица  неособенная.
неособенная.
Пример 3. Пусть X = R 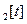
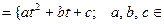 R
R 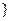 – пространство многочленов с вещественными коэффициентами от буквы
– пространство многочленов с вещественными коэффициентами от буквы 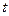 степени не выше второй. Отображение A: X ®X, сопоставляющее каждому многочлену
степени не выше второй. Отображение A: X ®X, сопоставляющее каждому многочлену 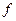 ÎX его производную
ÎX его производную 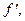 т.е.
т.е. 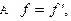 является линейным оператором.
является линейным оператором.
Задача 2. Пусть A: X ®Y - изоморфизм линейных пространств и 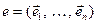 - базис пространства X.. Докажите, что тогда
- базис пространства X.. Докажите, что тогда
A 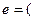 A
A 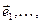 A
A 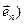 базис пространства Y. Таким образом, если X
базис пространства Y. Таким образом, если X 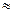 Y, то
Y, то 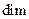 X
X 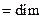 Y.
Y.
Задача 3. Докажите, что отображение A: X ® K 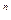 , заданное формулойA (
, заданное формулойA ( )=
)=  , где
, где  - базис линейного пространства X над полем K, естьизоморфизм линейных пространств.
- базис линейного пространства X над полем K, естьизоморфизм линейных пространств.
Задача 4. Докажите, что если X 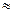 Y, то Y
Y, то Y 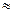 X.
X.
Задача 5. Докажите, что если X 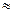 Y, Y
Y, Y 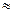 Z, то X
Z, то X 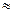 Z,
Z,
Задача 6. Докажите, что если 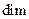 X
X 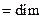 Y, то X
Y, то X 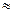 Y.
Y.
Задача 7. Докажите, что K 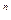
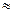 K
K 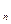 .
.
Действия над линейными операторами.
Пусть X– линейное пространство над полем K.
Определение 1. Пусть A, B 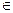 L (X). Суммой линейных операторов A и B, действующих в пространстве X называют отображение, действующее из X в X, обозначаемое
L (X). Суммой линейных операторов A и B, действующих в пространстве X называют отображение, действующее из X в X, обозначаемое 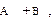 и такое, что (
и такое, что (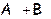 )
) 

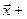
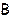
 для любого вектора
для любого вектора  ÎX.
ÎX.
Определение 2. Произведением числа l Î K на линейный оператор A 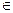 L (X) называют отображение, действующее из X в X, обозначаемое lA, такое, что (lA)
L (X) называют отображение, действующее из X в X, обозначаемое lA, такое, что (lA)  = lA
= lA  для любого вектора
для любого вектора  ÎX.
ÎX.
Определение 3. Произведением линейного оператора A 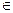 L (X) на линейный оператор
L (X) на линейный оператор 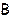
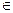 L (X) называют отображение, действующее из X в X и обозначаемое через
L (X) называют отображение, действующее из X в X и обозначаемое через 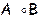 или
или 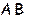 такое, что (
такое, что (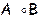 )
) 
 (
(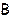 (
(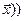 для любого вектора
для любого вектора  ÎX.
ÎX.
Схематически это можно изобразить так:
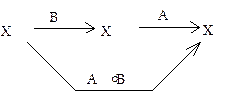
Замечание 1. Произведение отображения 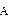 на
на 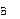 называют также композицией или суперпозицией этих отображений.
называют также композицией или суперпозицией этих отображений.
Замечание 2. Знак “ 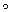 ” иногда для краткости будем опускать.
” иногда для краткости будем опускать.
Лемма 1. Пусть X – линейное пространство над полем K. Если 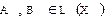 ,
, 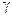 Î K, то
Î K, то 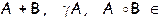
 . Другими словами, сумма двух линейных операторов, произведение линейного оператора на число, произведение двух линейных операторов, действующих в X, также являются линейными операторами.
. Другими словами, сумма двух линейных операторов, произведение линейного оператора на число, произведение двух линейных операторов, действующих в X, также являются линейными операторами.
Доказательство заключается в проверке условия определения 2 §1для указанных операторов. Мы проведем эту проверку лишь для суммы и произведения операторов. Остальное рекомендуется проверить самостоятельно. Пусть  X и
X и  K. Тогда получаем:
K. Тогда получаем:
(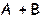 )
) 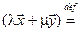

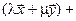
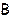
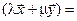 (
(

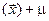

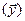 )
) 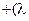
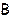
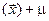
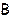
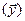 )=
)=
=  (
(
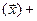
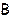
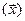 )+
)+  (
(
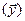 )
) 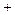
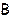
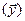 )=
)=  (
(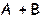 )
) 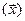 +
+  (
(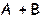 )
) 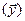
(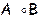 )
) 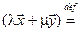
 (
(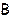
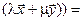
 (
(
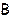
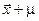
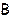
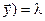
 (
(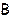
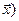
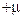
 (
(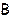
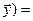
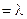 (
(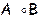 )
) 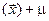 (
(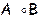 )
) 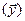 .
.
Здесь мы воспользовались линейностью операторов A, B, определениями 1 и 3, а также аксиомами линейного пространства.
Следствие. Доказанное утверждение означает, что на множестве 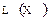 линейных операторов, действующих в X, определены операции сложения, умножения на число и умножения операторов.
линейных операторов, действующих в X, определены операции сложения, умножения на число и умножения операторов.
Определение 4. Нулевым оператором называют такой оператор, действующих в пространстве X и обозначаемый через O, что O 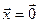 для любого вектора
для любого вектора  ÎX. Очевидно
ÎX. Очевидно 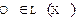 .
.
Определение 5. Тождественным или единичным оператором будем называть оператор, обозначаемый черезE, и такой, что E 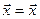 для любого вектора
для любого вектора  ÎX. Очевидно,
ÎX. Очевидно, 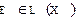 .
.
Определение 6. Два отображения A: X ®Y и B: X ®Y равны, если A  =B
=B  для любого вектора
для любого вектора  ÎX. Аналогично определяется равенство двух операторов.
ÎX. Аналогично определяется равенство двух операторов.
Теорема 1. Множество 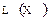 линейных операторов, действующих в линейном пространстве X над полем K, является линейным пространством над K относительно операций сложения и умножения на числа поля K, т.е. для любых операторов
линейных операторов, действующих в линейном пространстве X над полем K, является линейным пространством над K относительно операций сложения и умножения на числа поля K, т.е. для любых операторов 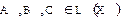 и любых l, m Î K справедливы равенства:
и любых l, m Î K справедливы равенства:
1) A +B = B +A;
2) (A +B) +C =A + (B +C);
3) A +O =A;
4) A + (–1)A =O;
5) 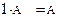 ;
;
6) l(A +B) = lA + lB;
7) (l + m)A =lA + mA;
8) (lm)A = l(mA);
Доказательство этих равенств основано на определениях 1, 2, 4, 6 и определении линейного пространства. Докажем для примера равенство 1: (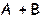 )
) 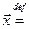

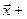
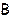

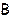
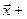


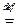 (
(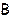 +
+  )
)  для любого вектора
для любого вектора  ÎX. По определению 6 это и означает, что
ÎX. По определению 6 это и означает, что 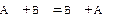 . Здесь использованы определение 1 и коммутативность сложения в линейном пространстве.
. Здесь использованы определение 1 и коммутативность сложения в линейном пространстве.
Совершенно аналогично доказывается равенство 2:
((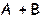 )+C)
)+C) 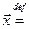 (
(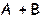 )
) 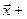 C
C 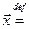 (
(
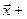
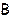
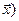 +C
+C 

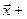 (
(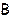
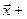 C
C 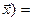
= 
 + (
+ (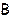 +C)
+C) 
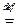 (A + (B +C))
(A + (B +C))  для любого вектора
для любого вектора  ÎX. По определению 6 это и означает, что (A +B) +C =A + (B +C). Здесь использованы определение 1, коммутативность и ассоциативность сложения в линейном пространстве. Остальные равенства предлагается доказать самостоятельно.
ÎX. По определению 6 это и означает, что (A +B) +C =A + (B +C). Здесь использованы определение 1, коммутативность и ассоциативность сложения в линейном пространстве. Остальные равенства предлагается доказать самостоятельно.
Теорема 2. Для любых операторов 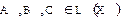 и любого l Î K справедливы равенства:
и любого l Î K справедливы равенства:
1)  (ассоциативность умножения);
(ассоциативность умножения);
2) 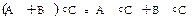 (левая дистрибутивность);
(левая дистрибутивность);
3) 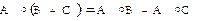 (правая дистрибутивность);
(правая дистрибутивность);
4) 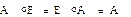 (существование единицы);
(существование единицы);
5) 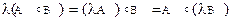 .
.
6) 
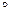 O =O
O =O 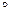
 =O.
=O.
Докажем лишь равенство 1, т.к. все остальные проверяются аналогично, что рекомендуется сделать самостоятельно.
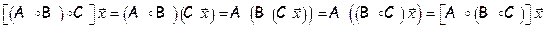
для любого вектора  ÎX, что и означает справедливость равенства 1.
ÎX, что и означает справедливость равенства 1.
Замечание 1. Из теоремы 2 следует, что для любого оператора 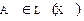 справедливо равенство
справедливо равенство 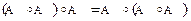 . Таким образом, способ расстановки скобок в произведении
. Таким образом, способ расстановки скобок в произведении 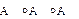 не имеет значения. Это произведение называют третьей степенью линейного оператора
не имеет значения. Это произведение называют третьей степенью линейного оператора 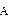 и обозначают так:
и обозначают так: 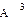 .
.
Точно так же независимо от способа расстановки скобок в произведении 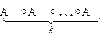 получаем один и тот же линейный оператор, который называют k-ой степенью оператора
получаем один и тот же линейный оператор, который называют k-ой степенью оператора 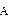 и обозначают так:
и обозначают так: 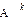 (здесь
(здесь 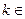 N). По определению считают, что
N). По определению считают, что 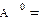 E.
E.
Таким образом, по определению 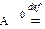 E;
E; 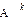
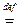
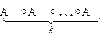 (здесь
(здесь 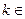 N).
N).
Задача. Докажите, что для любых 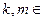 N
N 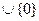 справедливы равенства
справедливы равенства
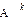
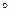
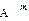 =
= 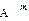
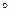
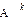 =
= 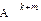 ; (
; (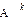
 =(
=(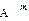
 =
= 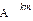 .
.