Пусть 
 – базис линейного пространства X над K,
– базис линейного пространства X над K,  и пусть известно действие оператора A на каждом из базисных векторов, т.е. известны векторы
и пусть известно действие оператора A на каждом из базисных векторов, т.е. известны векторы 
 ,
, 
 , ¼,
, ¼, 
 . Тогда известно и действие оператора A на любом векторе
. Тогда известно и действие оператора A на любом векторе  .
.
В самом деле, 


 =
= 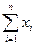

 Таким образом, чтобы задать линейный оператор A, достаточно задать векторы
Таким образом, чтобы задать линейный оператор A, достаточно задать векторы 
 ,
, 
 , ¼,
, ¼, 
 .
.
Определение 1. Пусть 
 – базис X,
– базис X,  . Разложим векторы
. Разложим векторы 
 ,
, 
 , ¼,
, ¼, 
 по базису
по базису  :
:


 ,
,
..............



Матрицу 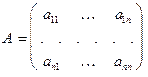 , столбцами которой являются координатные столбцы векторов
, столбцами которой являются координатные столбцы векторов 
 ,
, 
 , ¼,
, ¼, 
 в базисе
в базисе  , будем называть матрицей линейного оператора A в базисе
, будем называть матрицей линейного оператора A в базисе  и обозначать так: [A ]
и обозначать так: [A ]  .
.
Кратко определение матрицы линейного оператора в базисе  можно записать так:
можно записать так:
[A ] 
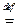 ([ A
([ A  ]
]  [A
[A  ]
] 
 [A
[A  ]
]  )
)
Замечание 1. Матрица линейного оператора в данном базисе определена однозначно, т.к. координаты вектора в данном базисе определены единственным образом.
Замечание 2. Очевидно, матрица единичного оператора в любом базисе – единичная, т.е.: [E ]  .
.
Замечание 3. Очевидно, матрица нулевого оператора в любом базисе – нулевая, т.е.: [O ]  .
.
Пример 1. Найдем матрицу оператора дифференцирования из примера 3 в базисе  .
.

Следовательно, [A ]  =
=  .
.
Пример 2. Найдем матрицу линейного оператора A, действующего в пространстве квадратных вещественных матриц второго порядка, т.е. в пространстве X  (R). Пусть
(R). Пусть  и A
и A  для любой матрицы
для любой матрицы  X. Оператор A - линейный, т.к.
X. Оператор A - линейный, т.к.
A  A
A 
 A
A  для любых чисел
для любых чисел  R и для любых матриц
R и для любых матриц  X
X  (R).
(R).
Обозначим через 
 базис пространства X из матриц
базис пространства X из матриц
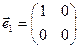 ,
,  ,
,  ,
,  .
.
Найдём матрицы 
 ,
, 
 ,
, 
 ,
, 
 и разложим их по базису
и разложим их по базису  :
:

 =
= 

 =
= 

 =
= 

 =
= 
Следовательно, матрица оператора A в базисе  найдена: [A ]
найдена: [A ] 

Теорема 1. Пусть 
 – базис линейного пространства X над полем K. Отображение
– базис линейного пространства X над полем K. Отображение


 (K), заданное формулой
(K), заданное формулой 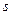 (
( ) =[A ]
) =[A ]  для любого
для любого  , является взаимно однозначным. Другими словами, каждая квадратная матрица порядка
, является взаимно однозначным. Другими словами, каждая квадратная матрица порядка  с элементами из поля K есть матрица единственного линейного оператора, действующего в пространстве X в базисе
с элементами из поля K есть матрица единственного линейного оператора, действующего в пространстве X в базисе  .
.
Доказательство. Как уже было отмечено выше, каждому линейному оператору по указанному правилу ставится в соответствие единственная квадратная матрица порядка  .
.
Покажем, что для любой матрицы 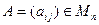 (K) существует, и притом единственный, линейный оператор
(K) существует, и притом единственный, линейный оператор  такой, что [A ]
такой, что [A ]  =
=  .
.
1. Докажем сначала существование такого линейного оператора. Зададим оператор  формулой
формулой 

 для любого вектора
для любого вектора  . Или, что то же самое
. Или, что то же самое 

 . Покажем, что
. Покажем, что  . Для любых векторов
. Для любых векторов  X и любых чисел
X и любых чисел  K получаем:
K получаем:
A 
=  A
A  +
+  A
A  . Следовательно, по определению оператор
. Следовательно, по определению оператор  - линейный. Здесь мы использовали свойства координат векторов и свойства действий над матрицами.
- линейный. Здесь мы использовали свойства координат векторов и свойства действий над матрицами.
2. Покажем теперь, что [A ]  =
=  . Пусть
. Пусть  . По определению 1
. По определению 1
[A ]  =([ A
=([ A  ]
]  [A
[A  ]
] 
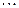 [A
[A  ]
]  ).
).
Следовательно, нужно доказать равенство [A  ]
]  =
= 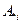 для всех
для всех  . Из определения оператора
. Из определения оператора  имеем:
имеем:

 , т.к. в координатном столбце вектора
, т.к. в координатном столбце вектора  в базисе
в базисе  число, стоящее на
число, стоящее на  -ом месте, равно единице, а остальные элементы равны нулю. Из единственности координат вектора в данном базисе получаем: [A
-ом месте, равно единице, а остальные элементы равны нулю. Из единственности координат вектора в данном базисе получаем: [A  ]
]  =
= 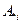 . Таким образом, [A ]
. Таким образом, [A ]  =
=  .
.
3. Докажем, наконец, единственность.
Пусть найдется такой оператор 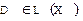 , что
, что  . Тогда, как следует из определения 1,
. Тогда, как следует из определения 1,
 ([
([ 
 ]
]  [
[ 
 ]
] 
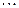 [
[ 
 ]
]  )=
)=  .
.
Следовательно, [ 
 ]
]  =
= 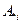 =[A
=[A  ]
]  , откуда и получаем равенства
, откуда и получаем равенства 
 =A
=A  для всех
для всех  .
.
Тогда для любого вектора 
имеем: 
 =
= 
 =
= 
 =
= 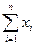

 =
= 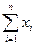

 =
= 
 =
= 
 . Следовательно, A =D
. Следовательно, A =D
и теорема полностью доказана.
Следствие. Из доказательства теоремы 1 следует равенство 

 =
=  ([A ]
([A ] 
 ).
).