Энергия светового поля. Лекция 4.
Поток энергии в световой волне. Интенсивность света.
Рассмотрим простейший случай: плоская монохроматическая волна 
распространяется вдоль оси 
. Согласно уравнениям Максвелла для вакуума
Умножим первое уравнение на 
, а второе – на 
и результаты сложим:
(1)
Введем объемную плотность энергии поля
Тогда (1) можно переписать в виде
, где 
(2)
Для выяснения физического смысла вновь веденного параметра 
рассмотрим поле в ограниченной параллелепипедом области пространства, как это показано на рис.1:
 |
Рис.1 Выделим объём параллелепипеда: 
- площадь основания, а - высота - вдоль 
. Проинтегрируем (2) по объему 
.
, (3)
где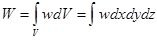 
- полная энергия поля внутри параллелепипеда; 
- его объем.
В вакууме изменение энергии в некотором объеме происходит исключительно за счет притока/оттока энергии через поверхность, его ограничивающую. Таким образом, в последнем выражении есть не что иное, как поток энергии световой волны.
Для плоской монохроматической волны равенство (3) тривиально, так как правая часть его обращается в 0 и 
, но для светового импульса 
- величина ненулевая за счёт пересечения разными модами основания параллелепипеда в разные моменты времени.
Обобщим результаты на случай произвольного поля, взаимодействующего к тому же с токами.
Для этого воспользуемся уравнениями Максвелла, добавив член, описывающий токи проводимости (
- плотность тока проводимости):
, 
(4)
Умножим скалярно первое уравнение в (4) на 
, а второе – на 
и вычтем из второго первое:
(5)
Воспользовавшись формулой 
и введя обозначения 
для объемной плотности энергии и 
для вектора потока энергии (вектора Пойнтинга) последнее выражение можно переписать в виде
(6)
Проинтегрируем (6) по произвольному замкнутому объему:
(7)
 |
Рис.2. Закон сохранения для системы заряженных частиц в поле световой волны.
Для точечных и дискретных зарядов: 
, где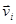 
- скорость 
- того заряда. Преобразуем интеграл в правой части (7) по теореме Гаусса:
, где: 
- ед. вектор к элементу 
поверхности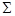 
(рис.2).
Используя уравнения движения точечного заряда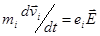 
и определение кинетической энергии 
можно показать, что 
.
Таким образом, для дискретных точечных зарядов (7) в вакууме окончательно преобразуется к виду:
(8)
Выражение (8) показывает, что скорость изменения энергии электромагнитного поля и кинетической энергии системы зарядов в некотором объеме равна потоку энергии через поверхность данного объема.
Для плоской монохроматической волны с учетом v = n c получим:
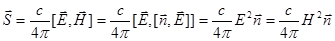(9)
Или 
(10)
Важнейший результат: в вакууме энергия плоской волны распространяется в направлении волнового вектора, то есть перпендикулярно волновому фронту.
Интенсивность света.
Рассмотрим плоскую монохроматическую волну вида , бегущую вдоль оси : 
. В этом случае модуль вектора Пойнтинга равен:
(11)
Последнее выражение содержит важнейший результат: поток энергии содержит два слагаемых – постоянный и быстро осциллирующий (на удвоенной оптической частоте). Так как измерительные приборы не могут отслеживать столь быстрые изменения (в оптике - 
), то реально измеримой величиной во всех оптических экспериментах является усредненная по большому (по сравнению с периодом оптических колебаний 
) промежутку времени величина модуля вектора Пойнтинга:
, - интенсивность света. (12)
где 
- постоянная времени, характеризующая фотоприемное устройство. Эта величина получила название
Для плоской монохроматической волны в вакууме 
. Для комплексной записи получается аналогичное выражение 
. Размерность интенсивности есть 
. В лазерной технике широко используется внесистемная единица 
.
Энергия, мощность, интенсивность световых пучков и импульсов.
Реальные световые пучки ограничены как в пространстве, так и во времени.
Квазиплоская волна описывается выражением 
,
а световой импульс - 
.
Тогда подставив значение поля в формулу для интенсивности (12) получим:
(13)
.
Полная мощность определяется интегрированием по поперечному сечению пучка:
(14)
Аналогично, полная энергия импульса есть:
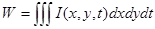(15)
Реально измеримыми величинами являются параметры мощности 
и энергии 
. Измерения проводятся устройствами, называемыми фотоприемниками. Эти устройства используют различные физические эффекты (фотоэффект, тепловое действие света и др.) для преобразования параметров светового пучка 
в пропорциональную электрическую величину – напряжение/ ток. Величина интервала времени , по которому производится усреднение в (12) может колебаться в широких пределах: 
, поэтому для реализации процесса измерения введены специальные величины - фотометрические величины.
Основные понятия фотометрии.
Для описания энергетических характеристик света, испускаемого нелазерными источниками, пользуются фотометрическими величинами.
Энергетические единицы измерения фотометрических величин величин.
Основные понятия:
Поток излучения
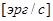
где 
- энергия, переносимая светом через некоторую поверхность.
Внимание! 
есть малый промежуток времени, но не бесконечно малая в математическом смысле. Интервал велик по сравнению с периодом колебаний световой волны.