Условие задания
Вычислить определенный интеграл функции у=f(х), заданной в табличном виде, методом трапеций и методом Симпсона. Вариант 5
Используя исходные данные:
Интервал интегрирования: a=14; b=24.
Число отрезков разбиения: N=10.
| x | |||||
| y | -8 | -4 |
Введение.
Для вычисления сложных математических моделей или решения сложных задач не всегда удается использовать аналитические методы расчета. В некоторых случаях для исследования того или иного явления не существует аналитических методов расчета. В таких случаях применяют численные методы, основанные на арифметических действиях над числами, и всегда заканчиваются числовым результатом.
Численные методы – это методы, которые заключаются в использовании арифметических и логических действий с числами. Для использования численных методов также применяются математические выражения, но они служат для указания арифметических действий и последовательности их выполнения. Для решения одной и той же задачи могут использоваться различные численные методы, которые отличаются сложностью, скоростью достижения конечного результата и степенью точности. Численные методы известны давно, но из-за громоздкости вычислений, получили применение с изобретением ЭВМ, что позволяет решает самые сложные задачи, требующие млн и млрд вычислений.
Численными методами можно рассчитывать задачи любой сложности, в том числе и определенный интеграл.
Определенный интеграл от функции f(х) на отрезке [a;b] называется предел интегральной суммы при неограниченном увеличении точек разбиения, при этом длина наибольшего из элементарных отрезков стремится к 0.
Считается, что, если функция f(х) непрерывна на отрезке [a;b], то предел интегральной суммы не зависит от их способа разбиения отрезка [a;b] на элементарные отрезки и не зависит выбора точек.
Глобальная интерполяция
В случае глобальной интерполяции отыскивается единый полином на всем интервале [ a, b ], т.е. строится полином, который используется для интерполяции функции f(x) на всем интервале изменения аргумента x. Будем искать интерполирующую функцию в виде полинома (многочлена) m –ой степени Pm (x) =a 0 +a 1 x+a 2 x 2 +a 3 x 3 +…+am xm. Какова должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции? Допустим, что заданы две точки: (x 0, f 0) и (x 1, f 1), т.е. N=1. Через эти точки можно провести единственную прямую, т.е. интерполирующей функцией будет полином первой степени P 1(x) =a 0 +a 1 x. Через три точки (N=2) можно провести параболу P 2(x) =a 0 +a 1 x+a 2 x 2 и т.д. Рассуждая таким способом, можно предположить, что искомый полином должен иметь степень N.
Для того, чтобы доказать это, выпишем систему уравнений на коэффициенты. Уравнения системы представляют собой условия интерполяции в при каждом x=xi:
Данная система является линейной относительно искомых коэффициентов a 0, a 1, a 2, …, aN. Известно, что СЛАУ имеет решение, если ее определитель отличен от нуля. Определитель данной системы
носит имя определителя Вандермонда. Из курса математического анализа известно, что он отличен от нуля, если xk ≠ xm (т.е. все узлы интерполяции различные). Таким образом, доказано, что система имеет решение.
Мы показали, что для нахождения коэффициентов
a 0, a 1, a 2, …, aN надо решить СЛАУ, что является сложной задачей. Но есть другой способ построения полинома N –й степени, который не требует решения такой системы.
Полином Лагранжа
Решение ищем в виде 
, где li (z) – базисные полиномы N –й степени, для которых выполняется условие: 
. Убедимся в том, что если такие полиномы построены, то LN(x) будет удовлетворять условиям интерполяции:
.
Каким образом построить базисные полиномы? Определим
, i= 0, 1, ..., N.
Легко понять, что
, и т.д.
Функция li (z) является полиномом N –й степени от z и для нее выполняются условия "базисности":
=0, i≠k;, т.е. k=1,…,i-1 или k=i+1,…,N.
.
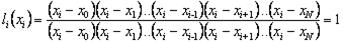Таким образом, нам удалось решить задачу о построении интерполирующего полинома N– й степени, и для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде компактной формулы: 
. Погрешность этой формулы можно оценить, если исходная функция g (x) имеет производные до N+ 1 порядка:
.
Из этой формулы следует, что погрешность метода зависит от свойств функции g (x), а также от расположения узлов интерполяции и точки z. Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях N <20. При бόльших N погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом N).
Рассмотрим частные случаи. Пусть N=1, т.е. заданы значения функции только в двух точках. Тогда базовые полиномы имеют вид:
, т.е. получаем формулы кусочно–линейной интерполяции.
Пусть N=2. Тогда: 
Метод трапеций
В этой формуле 
, т.е. площадь криволинейной трапеции, заменяется на площадь прямоугольной трапеции.
Формула трапеций получается путем замены подынтегральной функции интерполяционным полиномом первой степени:
.
Действительно
Тогда для всего отрезка [a,b] получим:
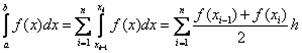
Можно показать, что формула трапеций имеет второй порядок точности.
Формулу трапеций можно записать в виде:
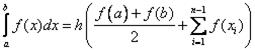
Метод Симпсона
При аппроксимации интеграла 
, функцию f(x)на отрезке 
заменяют параболой, проходящей через точки 
, где 
, т.е. используем для аппроксимации полином Лагранжа второй степени:
Следовательно, получаем формулу Симпсона
Можно показать, что формула Симпсона имеет четвертый порядок точности.
Расчетная часть
Численное интегрирование функции
Для интегрирования дан отрезок [а,в] с числом разбиения n
a=14; b=24 n=10
Тогда постоянный шаг будет равен
