Тема: Основные физические свойства жидкости
Задача 1
5 вариант.
Определить (рис.1) скорость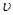 
равномерного скольжения прямоугольной пластины (a×b×c) по наклонной» плоскости под углом α =15 град, если между пластиной и плоскостью находится слой масла толщиной σ. Температура масла 30 ºС, плотность материала пластины 
.
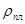Исходные данные к задаче: масло АМГ-10; а = 470 мм; b = 290 мм; с = 20 мм; σ = 0,4 мм; 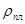= 260 кг/м3.
Решение
По формуле Ньютона:
.
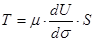Пластина скользит под воздействием силы F, обусловленной силой тяжести и направленной параллельно плоскости пластины, которая может быть выражена в виде:
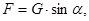
где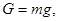 
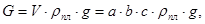- вес пластины.
Коэффициент динамической вязкости
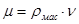.=260*0,00000696=0,0018 Па*с
Так как толщина слоя масла мала, можно считать, что скорости частиц жидкости в нем изменяются по прямолинейному закону. Следовательно, градиент скорости можно выразить как
.
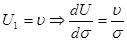При равномерном движении пластины работа, совершаемая силой F, расходуется на преодоление работы сил вязкого трения Т, т.е.
,
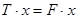поэтому по абсолютной величине эти силы будут равны.
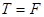или 
.
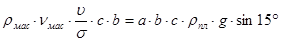Выражаем скорость скольжения пластины:
.
.
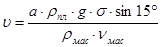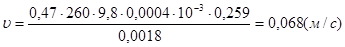Скорость равномерного скольжения прямоугольной пластины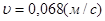 
.
Тема: Определение силы гидростатического давления жидкости на плоские и криволинейные поверхности
Задача 2
5 вариант.
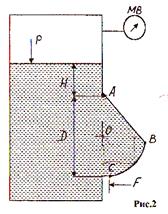
Закрытый резервуар (рис. 2) заполнен дизельным топливом, температура которого равна 20ºС. В вертикальной стенке резервуара имеется прямоугольное отверстие (D×b), закрытое крышкой ABC. Крышка может вращаться вокруг горизонтальной оси А. Криволинейная часть крышки ВС имеет центр кривизны в точке О. Мановакуумметр MB показывает манометрическое давление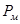 
или вакуум 
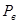над поверхностью жидкости. Расстояние от т.А до поверхности жидкости обозначено Н. Определить усилие F, которое необходимо приложить к нижней части крышки (т.С), чтобы крышка не открывалась. Силой тяжести крышки пренебречь. На схеме показать векторы действующих сил.
Исходные данные к задаче: 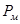= 4,68 кПа; D = 1,1 м: b = 1,75 м; Н = 0,95 м.
Решение
гидростатическое давление жидкость
Задачу удобно решать с помощью пьезометрической плоскости N – N. Положение N – N определяется путем расчета расстояния от этой плоскости до уровня жидкости в сосуде.
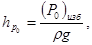
где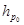 
- пьезометрическая высота;
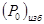- избыточное давление;
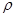- плотность жидкости;
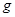- ускорение силы тяжести.
.
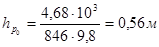Определяем величину и направление вектора составляющих сил (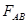
и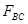 
) полной силы (
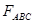) гидростатического давления: 
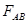- сила, действующая на плоскую часть крышки АВ; 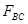- сила, действующая на цилиндрическую часть крышки ВС.
Определяем силу, с которой жидкость действует на поверхность АB:
,
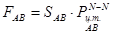где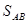 
- площадь площадки АВ;
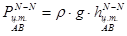- избыточное давление в центре тяжести горизонтальной проекции АВ;
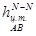- расстояние от центра тяжести площадки АВ до пьезометрической плоскости по вертикали;
,
,
,
.
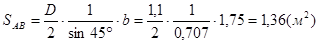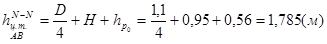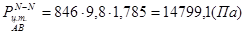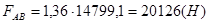Вектор силы 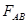приложен к площадке AB перпендикулярно в точке, называемой центром давления (ЦД), которая смещена от центра тяжести площадки АВ в плоскости этой площадки на величину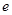 
± 
,
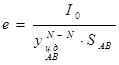где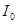 
- момент инерции площадки АВ относительно своей центральной оси;
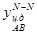- расстояние от центра тяжести площадки АВ до пьезометрической плоскости (в плоскости площадки АВ);
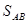- площадь площадки;
"+" - центр тяжести площадки АВ лежит ниже пьезометрической плоскости (откладывается вниз от центра тяжести АВ);
"-" - центр тяжести площадки АВ лежит выше пьезометрической плоскости (откладывается вверх от центра тяжести).
,
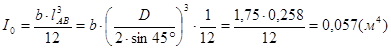где D, b – длина и ширина отверстия.
,
.
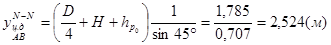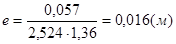Определение величины силы гидростатического давления 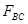осуществляется по соотношению:
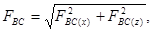
где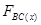 
- горизонтальная составляющая, равная силе, приложенной к вертикальной проекции
криволинейной поверхности ВС, т.е. к площадке ОС;
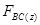- вертикальная составляющая, равная весу тела давления.
Горизонтальная составляющая силы 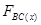, приложенная к вертикальной проекции криволинейной поверхности ВС, определяется как
,
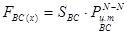где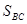 
- площадь вертикальной проекции ВС;
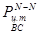- избыточное давление в центре тяжести вертикальной проекции ВС.
,
,
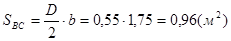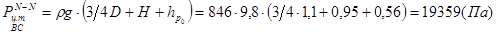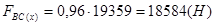
Вертикальная составляющая силы 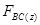определится как
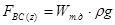
где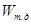 
- объем тела давления, действующего на криволинейную поверхность ВС;
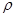- плотность жидкости, заполняющей тело давления.
,
,
.
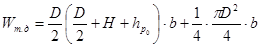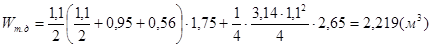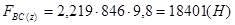Вектор составляющей 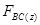направлен вниз, если объем тела давления строится со "смоченной" поверхности, и направлен вверх, если объем тела давления строится с "несмоченной" поверхности.
Величина полной силы гидростатического давления равна:
.
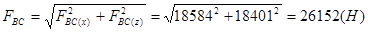Вектор результирующей силы будет проходить через т.О под углом α к вертикали, косинус которого:
, 
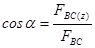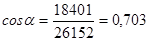
(α=45º9’).
Для определения силы F, которую необходимо приложить к т.С, чтобы крышка ABC была прижата к отверстию в стенке резервуара, составляем уравнение равновесия системы, на которую действуют несколько сил относительно т.А:
,
,
,
.
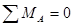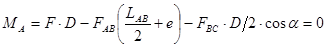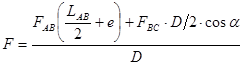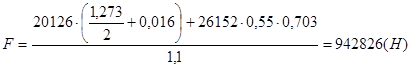Усилие, которое необходимо приложить к нижней части крышки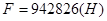 
.
Тема: Гидравлический расчет трубопроводов
Задача 3
5 вариант.
Резервуары А и В с постоянными и одинаковыми уровнями воды соединены системой труб, приведенные длины которых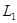 
, 
, 
, 
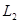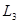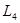, а диаметры соответственно 
, 
, 
, 
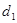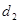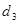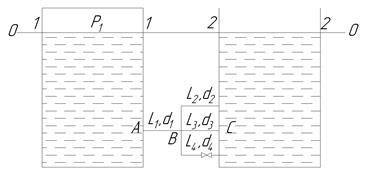
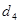(рис.3).
Определить: 1. При каком избыточном давлении Р над поверхностью воды в резервуаре А расход в трубе 4 будет равен Q?
Каков при этом суммарный расход воды (из резервуара А в резервуар В)?
Задачу решать аналитическим методом, приняв: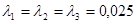 
, 
.
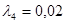Исходные данные к задаче: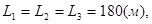 
, 
, 
, 
.
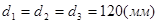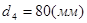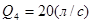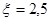Решение
Решаем задачу с помощью уравнения Бернулли:
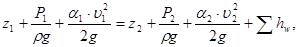
где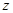 
- геометрический напор;
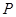- давление в центре тяжести сечения;
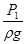- пьезометрический напор - вертикальное расстояние между центром тяжести сечения и уровнем жидкости в пьезометре;
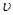- средняя скорость потока в сечении;
α - коэффициент Кориолиса;
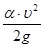- скоростной напор в сечении;
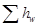- гидравлические потери напора, которые равны сумме потерь напора по длине трубопровода и потерь напора в местных сопротивлениях.
Выбираем два сечения в потоке так, чтобы в них было известно наибольшее число входящих в уравнение Бернулли гидродинамических параметров (в нашем случае удобно выбрать сечения 1-1 и 2-2).
Намечаем горизонтальную плоскость сравнения 0-0 (в нашем случае удобно выбрать плоскость, проходящую через центры тяжести сечений 1-1 и 2-2).
Для выбранных сечений относительно плоскости сравнения составляем уравнение Бернулли и определяем отдельные его слагаемые.
Записываем уравнение Бернулли для сечения 1-1 и 2-2 относительно плоскости сравнения 0-0, проходящей через эти сечения, получаем:
.
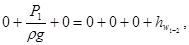
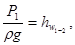
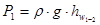Потери на участке 1-2 складываем из потерь на участке АВ и ВС, т. е.
.
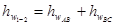Потери на участке ВС находим по II-й водопроводной формуле:
,
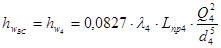где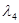 
- коэффициент вязкого трения (коэффициент Дарси);
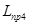- приведенная длина 4-го участка, имеющего n местных сопротивлений и действительную длину ;
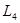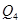- расход в 4-й трубе;
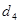- диаметр 4-й трубы.
, 
,
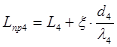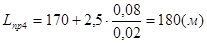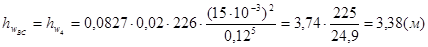
Потери на участке АВ находим также по II-й водопроводной формуле:
,
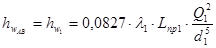Т. к. на первом участке нет местных сопротивлений, то приведенная длина трубы равна действительной ее длине:
.
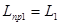Определяем суммарный расход воды в трубопроводе:
,
, 
.
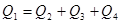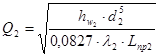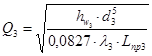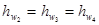(т. к. потери напора на параллельно включенных участках одинаковы по величине).
Следовательно,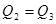 
(т.к.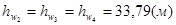 
, 
, 
, 
).
.
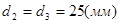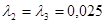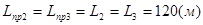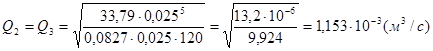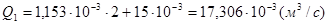
Потери на участке АВ получаются равными:
.
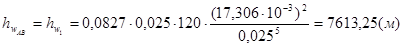Потери на участке 1-2 получаются равными:
.
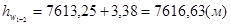Необходимое давление Р над поверхностью жидкости в резервуаре А:
.
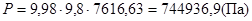МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ