Многошаговые методы
Решения задачи коши
Содержание
9.1. Метод “предиктор-корректор” 2
9.2. Общая формулировка многошаговых методов 4
9.3. Устойчивость и сходимость разностных методов 7
9.1. Метод “предиктор-корректор”
В одношаговых методах значение y n+1 определяется лишь значениями t n, y n и значением шага приращения аргумента h. В многошаговых методах используется также информация в предыдущих точках y n-1, y n-2,
Многошаговые методы строятся на равномерной сетке
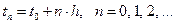 , где h – шаг сетки.
, где h – шаг сетки.
Обозначим: 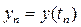 ,
, 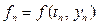 .
.
Линейный m -шаговый метод можно описать формулой:
 . (9.1)
. (9.1)
Многошаговые методы не являются самостартующими. Для использования m -шагового метода необходимо предварительно задать m предыдущих значений y. Однако после того как многошаговый метод стартует, он работает быстрее, чем одношаговый. Например, при использовании метода Рунге-Кутта-Фельберга на каждом шаге приращения аргумента требуется шесть раз вычислять правую часть дифференциального уравнения  . В то же время при использовании многошагового метода на каждом шаге приращения вычисляется только одно новое значение правой части.
. В то же время при использовании многошагового метода на каждом шаге приращения вычисляется только одно новое значение правой части.
Еще одним ограничением использования многошаговых методов является наличие равномерной сетки. Однако это ограничение легко преодолевается, например, с помощью интерполяции.
Многошаговые методы используются при решении жестких уравнений.
Порядок многошагового метода может выбираться автоматически и динамически изменяться.
Если 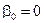 , то многошаговый метод называется явным.
, то многошаговый метод называется явным.
Если  , то метод является неявным, т.к. в случае невырожденного дифференциального уравнения f n+1 зависит от y n+1. Следовательно, на каждом шаге приращения аргумента необходимо решать уравнение относительно y n+1. Трудности, возникающие при использовании неявных методов, компенсируются тем, что эти методы являются более точными и более устойчивыми.
, то метод является неявным, т.к. в случае невырожденного дифференциального уравнения f n+1 зависит от y n+1. Следовательно, на каждом шаге приращения аргумента необходимо решать уравнение относительно y n+1. Трудности, возникающие при использовании неявных методов, компенсируются тем, что эти методы являются более точными и более устойчивыми.
Частным случаем многошаговых методов являются методы Адамса:
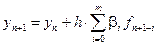 (9.2)
(9.2)
Методы Адамса также могут быть явными и неявными.
Трудности использования неявной формулы преодолевается в методе Предиктор–Корректор. В этом методе значение неизвестной функции в каждой точке сетки вычисляется дважды. Сначала вычисляется новое значение неизвестной функции 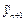 с помощью менее точной явной формулы – формулы предиктор. Затем это значение уточняется с помощью неявной формулы – формулы корректор; при этом для вычисления величины
с помощью менее точной явной формулы – формулы предиктор. Затем это значение уточняется с помощью неявной формулы – формулы корректор; при этом для вычисления величины  используется найденное значение
используется найденное значение 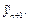
Простейшим примером метода Предиктор–Корректор является второй модифицированный метод Эйлера, который можно описать с помощью последовательности формул:
 – предиктор,
– предиктор,
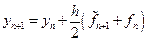 – корректор.
– корректор.
Метод Эйлера является одношаговым методом. Для построения многошаговых методов вновь используем утверждение: решение задачи Коши эквивалентно решению интегрального уравнения
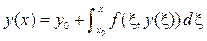 . (9.3)
. (9.3)
Для приближенного решения задачи Коши аппроксимируем подынтегральную функцию в формуле (9.3) с помощью интерполяционного многочлена. Интерполяционный многочлен Ньютона степени m для интерполирования назад от точки x n можно записать следующим образом
 . (9.4)
. (9.4)
В формуле (9.4) 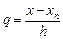 , а
, а  обозначает конечную разность порядка k, отсчитываемую от точки x i:
обозначает конечную разность порядка k, отсчитываемую от точки x i:
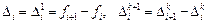 ,
,  . (9.5)
. (9.5)
Обозначим:
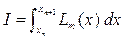 (9.6)
(9.6)
Найдем вначале формулы для двухшагового метода m =2. В качестве подынтегральной функции в формуле (9.6) будем использовать интерполяционный многочлен Ньютона первой степени.
Для вывода формулы предиктор вычислим интеграл (9.6) на отрезке экстраполяции  . После замены переменной интегрирования получим
. После замены переменной интегрирования получим
 (9.7)
(9.7)
и  .
.
Подставив найденное значение интеграла в формулу (9.3), получим экстраполяционную формулу – формулу предиктор:
 (9.8)
(9.8)
При выводе формулы корректор используем многочлен Ньютона для интерполирования от точки x n+1. Соответственно, в формуле (9.7) все индексы нужно увеличить на 1, а пределы интегрирования изменить на 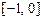 :
:
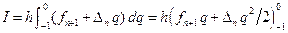 (9.9)
(9.9)

Подставив найденное значение интеграла в формулу (9.3), получим интерполяционную формулу – формулу корректор:
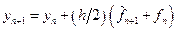 (9.10)
(9.10)
Пример 9.1
С помощью двухшагового метода предиктор-корректор найдем решение начальной задачи:
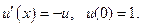
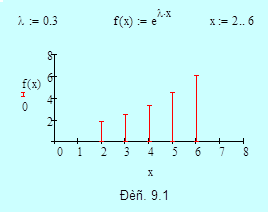
Точное решение представляет собой экспоненту 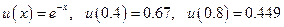 .
.
Выберем шаг приращения 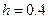 .
.
Начальное условие: 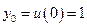 .
.
Дополнительное условие:  .
.
С помощью формул (9.8) и (9.10) вычислим значение 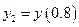 .
.
По формуле предиктор получаем: 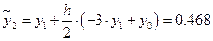 .
.
По формуле корректор уточняем решение:  .
.
Для сравнения приведем расчеты значения 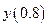 , исходя из точки
, исходя из точки  , по формуле второго модифицированного метода Эйлера:
, по формуле второго модифицированного метода Эйлера:
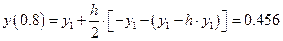 .
.
На практике обычно применяется четырехшаговый метод Адамса. Найдем формулы для четырехшагового метода. Повторяем весь ход рассуждений, использованных при выводе формул 2-шагового метода, но в отличие от предыдущего используем теперь многочлен Ньютона третьей степени.
Вывод формулы предиктор.
Вычисляем интеграл

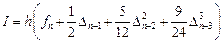
Подставив найденное значение интеграла в формулу (9.3), получим с учетом выражений (9.5) для конечных разностей формулу предиктор – формулу Адамса-Башфорта (Adams-Bashforth):
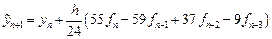 (9.11)
(9.11)
Вывод формулы корректор.
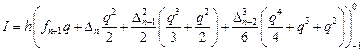
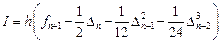
Аналогично предыдущему с учетом (9.3) и (9.5) получим формулу корректор – формулу Адамса-Мультона (Adams-Moulton):
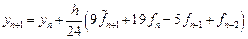 (9.12)
(9.12)
Общая формулировка многошаговых методов
Для решения задачи Коши
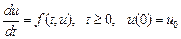 (9.13)
(9.13)
введем сетку с постоянным шагом  и сеточные функции:
и сеточные функции:
 – точное решение задачи Коши;
– точное решение задачи Коши;
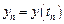 – приближенное решение;
– приближенное решение;
 .
.
Линейным m-шаговым разностным методом называется система разностных уравнений
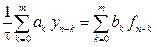 , (9.14)
, (9.14)
где 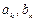 – числовые коэффициенты, независящие от n, причем
– числовые коэффициенты, независящие от n, причем 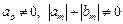 .
.
Уравнение (9.14) представляет собой рекуррентное соотношение, выражающее новое значение 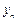 через найденные ранее значения
через найденные ранее значения 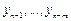 .
.
Заметим, что коэффициенты уравнения (9.14) определены с точностью до множителя. Для устранения неоднозначности будем считать, что выполнено условие нормировки
 (9.15)
(9.15)
Метод называется явным, если  .
.
Если 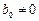 , то метод называется неявным. В этом случае для нахождения
, то метод называется неявным. В этом случае для нахождения 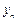 приходится решать нелинейное уравнение
приходится решать нелинейное уравнение
 .
.
Это уравнение можно решить методом Ньютона, в качестве начального приближения взяв  .
.
Погрешностью аппроксимации на решении или невязкой разностного метода (9.14) называется функция
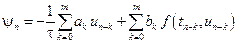 (9.16)
(9.16)
Функция невязки получается в результате подстановки точного решения дифференциального уравнения в разностное уравнение (9.14).

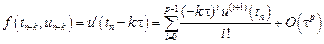
Подставим эти разложения в формулу для невязки

Изменим порядок суммирования. При этом во второй сумме будем суммировать по индексу i от 1 до p, соответственно уменьшив всюду индекс i на единицу.
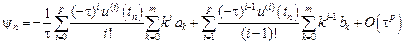
Объединим суммы, выделив в первой сумме отдельно слагаемое с j=0.
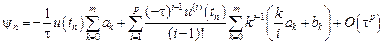
Отсюда следует, что погрешность метода будет иметь порядок p, если выполнены условия:
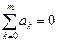 и
и 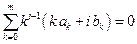 при
при  (9.17)
(9.17)
Заметим что, если в системе (9.17) отбросить последние s уравнений, то порядок метода понизится на s.
Итак, получили систему уравнений для коэффициентов a k, b k. К этим уравнениям нужно добавить еще условие нормировки (9.15): 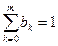 . Получаем, таким образом p+2 уравнений. Чтобы система уравнений не была переопределена, нужно, чтобы количество уравнений не превышало количество неизвестных.
. Получаем, таким образом p+2 уравнений. Чтобы система уравнений не была переопределена, нужно, чтобы количество уравнений не превышало количество неизвестных.
Для неявного метода имеем 2 m +2 неизвестных: 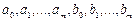 . Должно быть:
. Должно быть:
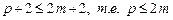
– для неявного метода порядок аппроксимации не превышает 2 m.
Для явного метода имеем 2 m +1 неизвестных: 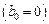 . Следовательно
. Следовательно 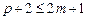 и порядок аппроксимации не превышает 2 m -1.
и порядок аппроксимации не превышает 2 m -1.
Преобразуем систему уравнений для коэффициентов a k, b k. С учетом условия нормировки уравнение 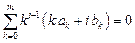 при
при 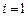 можно переписать в виде
можно переписать в виде 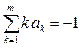 . Учтем также, что коэффициент a 0 входит только в одно уравнение, так что разрешим это уравнение относительно a 0.
. Учтем также, что коэффициент a 0 входит только в одно уравнение, так что разрешим это уравнение относительно a 0.
Окончательно получаем систему уравнений для коэффициентов линейного m -шагового разностного метода общего вида:
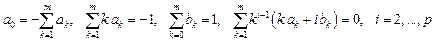 (9.18)
(9.18)
На практике часто используются методы Адамса, которые описываются формулой
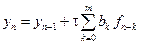 (9.19)
(9.19)
Для методов Адамса в системе (9.18) остаются только уравнения, определяющие коэффициенты b k.
 (условие нормировки) и уравнения:
(условие нормировки) и уравнения: 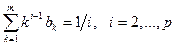 (9.20)
(9.20)
Имеем p уравнений. В случае неявного метода Адамса имеется m +1 неизвестных: 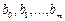 . Следовательно, наивысший порядок неявного метода равен p = m +1. В случае явного метода имеем m неизвестных, следовательно, максимальный порядок явного метода Адамса равен p = m.
. Следовательно, наивысший порядок неявного метода равен p = m +1. В случае явного метода имеем m неизвестных, следовательно, максимальный порядок явного метода Адамса равен p = m.
Пример 9.2
Рассмотрим варианты двухшаговых методов m =2. Максимальный порядок двухшагового метода равен p =4, так что можно написать следующую систему уравнений.

Ограничившись первыми четырьмя уравнениями этой системы, можно построить методы 2-го порядка. Если использовать пять уравнений, получим методы 3-го порядка. Система из шести уравнений определяет единственный двухшаговый метод 4-го порядка.
Варианты методов второго порядка.
1) Положим 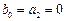 , тогда
, тогда 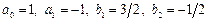 . Получаем явный метод Адамса:
. Получаем явный метод Адамса:  .
.
2) Положив 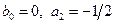 , получим метод Милна:
, получим метод Милна:  .
.
3) Положив 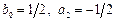 , построим неявный метод:
, построим неявный метод: 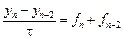 .
.
Варианты методов третьего порядка.
1) Положив  , получим явный метод
, получим явный метод 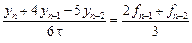 .
.
2) Если выбрать 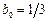 , построим неявный метод
, построим неявный метод  .
.
3) Выбрав 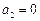 , получим неявный метод Адамса
, получим неявный метод Адамса 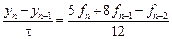 .
.
Метод четвертого порядка получим, используя все шесть уравнений:
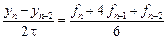
Пример 9.3.
 Построим трехшаговые методы Адамса.
Построим трехшаговые методы Адамса.
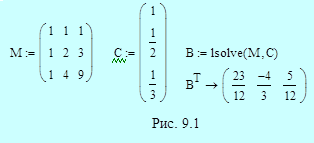
Явный трехшаговый метод имеет порядок p =3. В соответствии с формулами (9.20) для нахождения коэффициентов b k имеем систему уравнений, включающую условие нормировки и еще два уравнения для двух значений i:  .
.
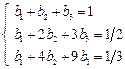
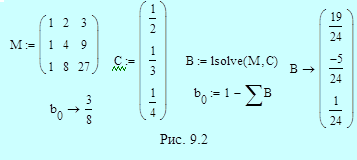 Решение этой системы в среде Mathcad приведено на рис. 9.1. Здесь M – матрица системы, C – столбец свободных коэффициентов. Функция lsolve находит решение системы линейных алгебраических уравнений. Вектор B включает найденное решение. Чтобы получить точные значения найденных коэффициентов используем знак аналитических вычислений (стрелка). Получаем явный трехшаговый метод Адамса третьего порядка:
Решение этой системы в среде Mathcad приведено на рис. 9.1. Здесь M – матрица системы, C – столбец свободных коэффициентов. Функция lsolve находит решение системы линейных алгебраических уравнений. Вектор B включает найденное решение. Чтобы получить точные значения найденных коэффициентов используем знак аналитических вычислений (стрелка). Получаем явный трехшаговый метод Адамса третьего порядка:
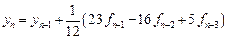
Неявный метод имеет четвертый порядок, и для коэффициентов 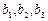 имеем систему из трех уравнений, где i принимает значения 2, 3 и 4. Значение b 0 определяем из условия нормировки. Решение в системе Mathcad приведено на рис. 9.2. Получаем вновь формулу Адамса-Мультона, которая ранее была найдена путем непосредственного вычисления интеграла от интерполяционного многочлена Ньютона (9.12):
имеем систему из трех уравнений, где i принимает значения 2, 3 и 4. Значение b 0 определяем из условия нормировки. Решение в системе Mathcad приведено на рис. 9.2. Получаем вновь формулу Адамса-Мультона, которая ранее была найдена путем непосредственного вычисления интеграла от интерполяционного многочлена Ньютона (9.12):
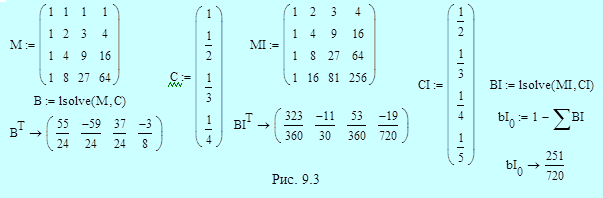 |
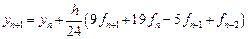
Пример 9.4. На рис. 9.3 приведено решение системы уравнений для коэффициентов явного и неявного четырехшаговых методов Адамса. Решение аналогично решению в примере 9.2 для трехшаговых методов. Обозначения M, C и B относятся к явному методу; обозначения MI, CI, BI и bI0 используются для описания неявного метода. Получаем в итоге:
- явный метод четвертого порядка (формула Адамса-Башфорта)
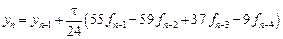 ;
;
- неявный метод пятого порядка
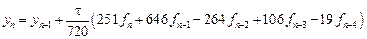 .
.