Элементы выборки не могут повторяться

В этом случае выборки могут отличаться друг от друга либо порядком, в котором выбираются элементы, либо самими элементами (составом элементов).

Например, из трех цифр 1, 2, 3 можно выбрать следующие комбинации из двух элементов: 12, 13, 21, 23, 31, 32.

В качестве первого элемента подобной выборки можно взять любой из k элементов исходного множества, но при выборе второго - уже (k- 1) элементов, третьего - (k- 2) элементов,…, r -го - (k- (r -1)) элементов. Таким образом, число различных выборок можно определить следующим образом:

N = k (k- 1)(k- 2)… (k- (r -1)). (2)

 

Такие комбинации называются размещениями без повторений и обозначаются символом . Выражение (2) можно упростить, умножив и разделив его на (k - r)!. Тогда получим:

 

Теорема 2. Если элементы выборки повторяться не могут, а сами выборки отличаются либо порядком, либо составом, то общее число различных выборок равно числу размещений без повторений А_k^r из k элементов по r:

(3)

 

ПРИМЕР 1.6. Сколько различных комбинаций из трех букв можно составить из букв слова "ромб", если каждую букву можно использовать только один раз?

РЕШЕНИЕ. Исходное множество состоит из 4 букв, выборка - из 3 букв. Элементы выборки не могут повторяться, поэтому:

N= =24.

 

ПРИМЕР 1.7. Сколько можно составить трехзначных чисел из нечетных цифр, если: а) каждую цифру можно использовать только один раз; б) если цифры могут повторяться?

РЕШЕНИЕ. Исходное множество состоит из 5 нечетных цифр {1, 3, 5, 7, 9}, выборка - из 3 цифр.

а) Если элементы выборки не могут повторяться, то:

N= = =60.

 

б) Если элементы выборки могут повторяться, то:

N= = 5³=125.

 

Рассмотрим частные случаи размещений:

Первый случай. Все возможные выборки могут состоять из одних и тех же элементов и отличаться друг от друга только порядком размещения элементов, то есть r=k. Тогда общее число выборок можно определить следующим образом:

 

Такие комбинации называются перестановками и обозначаются символом .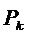

 

Теорема 3. Если выборки состоят из одних и тех же элементов и отличаются друг от друга только порядком, то общее число различных выборок равно числу перестановок из k элементов:

 

ПРИМЕР 1.8. Сколько можно составить трехзначных чисел из цифр 1, 2, 3, если: а) каждую цифру можно использовать только один раз; б) если цифры могут повторяться?

РЕШЕНИЕ. Исходное множество состоит из 3 цифр, выборка - также из 3 цифр.

а) Если элементы выборки не могут повторяться, то:

N= .

б) Если цифры могут повторяться, то:

N= 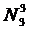= 3³=27.

 

ПРИМЕР 1.9. Сколькими способами можно расставить на полке 10 книг?

РЕШЕНИЕ. Исходное множество и выборка состоят из 10 книг. Тогда:

N=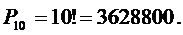

 

ПРИМЕР 1.10. Сколькими способами можно рассадить четырех человек в четырехместной каюте?

РЕШЕНИЕ. Исходное множество и выборка состоят из 4 элементов. Тогда:

N=

 

Второй случай. Рассмотрим выборки, в которых порядок размещения элементов не имеет значения, а сами выборки отличаются друг от друга только составом. Тогда общее число выборок можно определить следующим образом:

 

Такие комбинации называются сочетаниями и обозначаются символом .

 

Теорема 4. Если элементы выборки не повторяются, порядок размещения элементов в выборке не имеет значения, а выборки отличаются только составом, то общее число различных выборок равно числу сочетаний из k элементов по r:

 

Надо уметь отличать сочетания от размещений. Например, пусть в группе 25 студентов. Пять человек вышли из аудитории на перерыв. Сколько всех возможных групп из 5студентов, выбранных из 25 человек, можно составить?

Если 5 человек стоят в коридоре и беседуют, то совершенно неважно в каком порядке они стоят. Число всех возможных групп из 5 человек, выбранных из 25 человек, равно числу сочетаний из 25 по 5:

Если же студенты отправились в перерыве в буфет, то тогда важно, в каком порядке они стоят в очереди. Число всех возможных групп из 5 человек, выбранных из 25 человек, с учетом их размещения в очереди равно числу размещений из 25 по 5:

 

Свойства сочетаний:

 

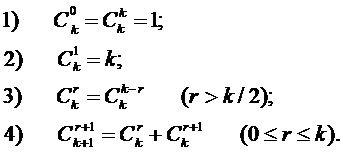
ПРИМЕР 1.11. Сколькими способами можно выбрать три шара из пяти?

РЕШЕНИЕ. Исходное множество состоит из 5 шаров, выборка - из 3 шаров. Порядок, в котором мы выбираем шары, значения не имеет, поэтому:

N= =10.

 

ПРИМЕР 1.12. Тринадцать студентов обменялись рукопожатиями. Сколько всего сделано рукопожатий?

РЕШЕНИЕ. Исходное множество состоит из 13 студентов, выборка - из 2 человек, поэтому:

N= =78.

 

1.2. Пусть даны два исходных множества, состоящих из k ₁и k ₂различных элементов. Необходимо определить число различных выборок N, составленных из элементов двух исходных множеств. В этом случае сначала делают выборку из одного множества и определяют N ₁ - число различных выборок, составленных из элементов первого исходного множества. Затем делают выборку из другого множества и определяют N ₂. Тогда общее число выборок:

N=N ₁× N ₂, (6)

где N ₁ и N ₂определяют по формулам (1), (3)-(5) в зависимости от конкретного смысла задачи.

 

ПРИМЕР 1.13. Из десяти красных роз и 8 белых роз нужно составить букет, содержащий две красных и три белых розы. Сколько можно составить таких букетов?

РЕШЕНИЕ. Одно исходное множество состоит из 10 красных роз, выборка - из 2 роз. Порядок, в котором мы выбираем розы, значения не имеет, поэтому:

N ₁ =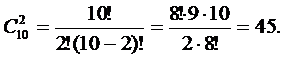

 

Другое исходное множество состоит из 8 белых роз, выборка - из 3 роз, поэтому:

N ₂ =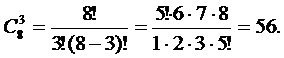

Тогда общее количество букетов N=N ₁× N ₂=45×56=2520.

 

ПРИМЕР 1.14. В урне лежат 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?

РЕШЕНИЕ. Одно исходное множество состоит из 10 белых шаров, выборка - из 4 белых шаров. Порядок, в котором мы выбираем шары, значения не имеет, поэтому:

N ₁ =

 

Другое исходное множество состоит из 5 черных шаров, выборка - из 3 шаров, поэтому:

N ₂ =

Тогда общее количество способов N=N ₁× N ₂=210×10=2100.

 

ПРИМЕР 1.15. Сколькими способами можно расставить на полке девять различных книг, чтобы определенные четыре книги стояли рядом?

РЕШЕНИЕ. Будем считать определенные 4 книги за одну. Тогда первое исходное множество состоит из 6 книг, выборка - также из 6 книг, т.е. исходное множество и выборка состоят из одних и тех же элементов. Эти шесть книг можно расставить на полке в разном порядке, поэтому:

N ₁ =

 

Другое исходное множество состоит из четырех определенных книг, выборка - из тех же книг, которые можно по-разному переставить между собой, поэтому:

N ₂ =

Тогда общее количество способов расстановки книг N=N ₁× N ₂=720×24=17280.