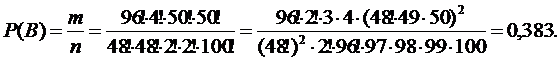ФОРМУЛ КОМБИНАТОРИКИ
Вероятность события А равна отношению числа исходов испытания m, в которых может появиться событие А, к общему числу n всех элементарных исходов испытания, образующих полную группу:

ПРИМЕР 2.1. Буквы Т, Е, И, Я, Р, О написаны на отдельных карточках. Ребенок берет карточки в случайном порядке и прикладывает одну к другой. Какова вероятность получить слова: а) "тор"; б) "теория"?
РЕШЕНИЕ. а) Пусть событие А - получение слова "тор". Элементарным исходом испытания является извлечение трех карточек из шести. Общее число всех исходов испытания равно числу размещений из 6 по 3, так как различные выборки могут отличаться как составом, так и порядком:
n= 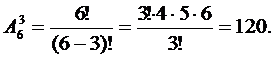
Слово "тор" можно получить только одним способом m =1. Тогда:

б) Пусть событие В - получение слова "теория". Элементарным исходом испытания является получение различных комбинаций из шести букв. Общее число всех исходов испытания равно числу перестановок из 6, так как различные выборки могут отличаться друг от друга только порядком:
n= 
Слово "теория" можно получить только одним способом m =1. Тогда:
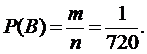
ПРИМЕР 2.2. Буква «а» написана на трех карточках, буква «н» - на двух карточках, буква «с» - на одной карточке. Ребенок берет карточки в случайном порядке и прикладывает одну к другой. Какова вероятность получить слово "ананас"?
РЕШЕНИЕ. Пусть событие А - получение слова "ананас". Как и в предыдущем случае, элементарным исходом испытания является получение различных комбинаций из шести букв. Общее число всех исходов испытания равно числу перестановок из 6, так как различные выборки могут отличаться друг от друга только порядком:
|
|
n= 
Слово "ананас" можно получить не одним способом, так как перестановка трех букв «а» и двух букв «н» не меняет это слово. Три карточки с буквой «а» можно расставить 6 способами:
m 1 = 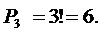
Две карточки с буквой «н» можно расставить 2 способами:
m 2 = 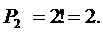
Карточку с буквой «с» можно расставить одним способом. Тогда: m = m 1 m 2 m 3 = 6×2×1=12.Следовательно:

ПРИМЕР 2.3. В урне находится 15 шаров, из них 9 красных и 6 синих. Какова вероятность того, что вынутые наугад два шара: а) оба красные; б) 1 красный, 1 синий?
РЕШЕНИЕ. а) Пусть событие А - извлечены два красных шара. Общее число всех исходов испытания равно числу способов, какими можно выбрать 2 шара из 15. Различные выборки могут отличаться друг от друга только составом (порядок не имеет значения), поэтому:
n= 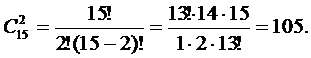
Число случаев, благоприятствующих событию А, равно числу сочетаний из 9 красных шаров по 2:
m= 
Следовательно:

б) Пусть событие В - извлечены один красный и один синий шар. Общее число всех исходов испытания, как и в предыдущем случае, равно n= 105. Для того чтобы подсчитать число случаев, благоприятствующих событию В, необходимо выбрать 1 шар из 9 красных (одно исходное множество) и 1 шар из 6 синих (другое исходное множество). Тогда:
m= m1×m2= 
Следовательно:
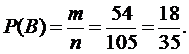
ПРИМЕР 2.4. В партии 50 деталей, из них 5 - бракованные. Какова вероятность того, что среди выбранных наудачу для проверки шести деталей две окажутся бракованными?
РЕШЕНИЕ. Пусть событие А - выбраны 2 бракованные детали и 4 небракованные. Общее число всех исходов испытания равно числу способов, какими можно выбрать 6 деталей из 50. Различные выборки могут отличаться друг от друга только составом (порядок не имеет значения), поэтому:
|
|
n= 
Для того чтобы подсчитать число случаев, благоприятствующих событию А, необходимо выбрать 2 детали из 5 бракованных (одно исходное множество) и 4 детали из 45 небракованных (другое исходное множество). Тогда:
m= m1×m2= 
Следовательно:

ПРИМЕР 2.5. В лифт на первом этаже девятиэтажного дома вошли 4 человека, каждый из которых может выйти независимо друг от друга на любом этаже с первого по девятый. Какова вероятность того, что все пассажиры выйдут: а) на шестом этаже; б) на одном этаже?
РЕШЕНИЕ. а) Пусть событие А - все пассажиры выйдут на шестом этаже. Каждый пассажир может выйти на восьми этажах (со второго по девятый этаж), то есть исходное множество состоит из 8 этажей. Выборка равна 4 этажам. Тогда общее число всех исходов испытания равно числу размещений с повторениями, так как элементы выборки могут повторяться (например, все четыре человека могут выйти на одном и том же этаже). Поэтому:
n= 
Число случаев, благоприятствующих событию А, равно m =1.
Следовательно:
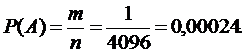
б) Пусть событие В - все пассажиры выйдут на одном этаже. Теперь событию В будут благоприятствовать m= 8 случаев (все пассажиры выйдут или на втором этаже, или на третьем, …, или на девятом этаже). Следовательно:

ПРИМЕР 2.6. В партии 100 изделий, из них 4 - бракованные. Партия произвольно разделена на две равные части, которые отправлены двум потребителям. Какова вероятность того, что все бракованные детали достанутся: а) одному потребителю; б) обоим потребителям поровну?
|
|
РЕШЕНИЕ. а) Пусть событие А - все бракованные изделия достанутся одному потребителю. Общее число всех исходов испытания равно числу способов выбрать 50 изделий из 100, то есть:
n= 
Событию А благоприятствуют случаи, когда из 50 изделий, отправленных одному потребителю, будет либо 46 стандартных из 96 и все 4 бракованных изделия, либо 50 стандартных из 96:

.
Следовательно:
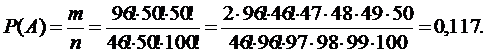
б) Пусть событие В - в каждой партии по 2 бракованных изделия. Теперь событию В будут благоприятствовать случаи, когда из 50 изделий, отправленных одному потребителю, будут 48 стандартных из 96 и 2 бракованных из 4, то есть:

Следовательно: