1. 
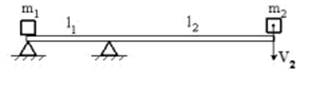Невесомая доска покоится на двух опорах. Правая опора делит длину доски в отношении 1:3 
. На правый конец доски падает тело массой m2=2 кг, скорость которого в момент удара была 
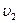. Если после удара это тело полностью теряет свою скорость, то тело массой m1=1 кг начнет двигаться со скоростью …
Варианты ответа:
А) 
Б) 
В) 
Г) 
2.Тело массой m1 вертикально падает на свободный конец рычага с плечом l 1 (l 1=2 l 2) и теряет свою скорость. Какую скорость приобретает масса m2 (m2 =4m1) после удара?
Варианты ответа:
А) 
Б) 
В) 
Г) 
3. 
Невесомая доска покоится на двух опорах. Правая опора делит длину доски на две неравные части. На правый конец доски падает тело массой m2=2 кг, теряя при ударе всю свою скорость. После удара первое тело массой m1=1 кг приобретает скорость V1, причемV1=3V2/2. В этом случае соотношение между l 1 и l 2 равно…
Варианты ответа:
А) 
б) 
в) 
г) 
4. Если момент инерции тела увеличить в 2 раза и скорость его вращения увеличить в 2 раза, то момент импульса тела…
Варианты ответа:
увеличится в раз
не изменится
увеличится в 8 раз
увеличится в 4 раза
5. Если момент инерции тела увеличить в 2 раза, а скорость его вращения уменьшить в 2 раза, то момент импульса тела…
Варианты ответа:
увеличится в раз
не изменится
увеличится в 8 раз
увеличится в 4 раз
6. 
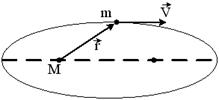Планета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массой М. Если – радиус-вектор планеты, то справедливым является утверждение…
Варианты ответа:
· Момент силы тяготения, действующей на планету, относительно центра звезды, не равен нулю.
· Момент импульса планеты относительно центра звезды при движении по орбите не изменяется.
· Для момента импульса планеты относительно центра звезды справедливо выражение: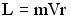 
.
|
|
- Человек, стоящий в центре вращающейся платформы, повернул вертикально расположенный в руках стержень в горизонтальное положение. В результате этого у системы:
А. Увеличится момент инерции.
Б. Увеличится угловая скорость.
В. Уменьшится период вращения.
Варианты ответа:
а. Только А; б. Только А и Б; в. Только Б и В; г. Только А и В.
- Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он повернет шест из вертикального положения в горизонтальное, то частота вращения в конечном состоянии
Варианты ответа:
а. уменьшится; б. увеличится; в. не изменится; г. не хватает данных для ответа.
9. Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за середину. Если он переместит шест вправо от себя, то частота вращения карусели в конечном состоянии…
Варианты ответа: а. уменьшится б.не изменится в.увеличится
- Человек сидит на вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест. Если он с помощью шеста выпрыгнет с карусели, то частота вращения…
Варианты ответа: а. уменьшится б. увеличится в. не изменится
- Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он переместит шест влево от себя, то частота вращения в конечном состоянии
Варианты ответа:
а. уменьшится; б. увеличится; в. не изменится; г. не хватает данных для ответа.
|
|
-
Вокруг неподвижной оси с угловой скоростью w1 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии R1 от оси вращения. Нить медленно освобождают, в результате чего шайба соскальзывает на расстояние R2=3R1 от оси вращения. Когда шайба окажется в положении 2, система будет вращаться с угловой скоростью…
Варианты ответа:
а. 
; б. 
; в. w2=3w1; г. w2=9w1.
- Вокруг неподвижной оси с угловой скоростью w1 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии R1 от оси вращения. Опустив нить, шайбу перевели в положение 2, результате чего шайба стала двигаться по окружности радиусом R2=2R1 с угловой скоростью…
Варианты ответа:
а. 
; б. 
; в. w2=4w1; г. w2=2w1.
- Вокруг неподвижной оси с угловой скоростью w1 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии R1 от оси вращения. Опустив нить, шайбу перевели в положение 2, результате чего шайба стала двигаться по окружности радиусом R2=
R1 с угловой скоростью…
Варианты ответа:
а. 
; б. 
; в. 
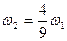; г. 
.
15. 
Два невесомых стержня длины b соединены под углом α1=120° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью ω. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до α2=90°. Система стала вращаться с угловой скоростью …
Варианты ответа:
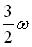
16. 
Два невесомых стержня длины b соединены под углом α1=60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью ω. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до α2=90°.
|
|
Система стала вращаться с угловой скоростью …
Варианты ответа:
2 ω ω/2 ω 
ω ω/
17. 
Два невесомых стержня длины b соединены под углом α1=180° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью ω. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до α2=60°.
Система стала вращаться с угловой скоростью …
Варианты ответа:
2 ω ω/2 ω 4 ω ω / 4
-
Экспериментатор, стоящий на неподвижной скамье Жуковского, получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью w. Если экспериментатор повернет ось вращения колеса на угол 180 градусов, то он вместе с платформой придет во вращение с угловой скоростьюw/5. Отношение момента инерции экспериментатора со скамьей к моменту инерции колеса равно…
Варианты ответа:
2,5 10 4 5