Если известно разложение в ряд по степеням z некоторой функции f(z), то из него легко получить разложение в степенной ряд любой функции вида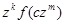 
, где k и m – некоторые натуральные числа.
Формулы Эйлера
Пользуясь разложением в степенной ряд функции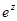 
, приведенное в конце предыдущей лекции, запишем разложение функции
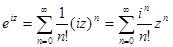
Нетрудно убедиться, что для степеней мнимой единицы i справедливы следующие равенства: четные степени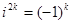 
, нечетные степени 
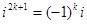. Таким образом, разбив ряд на сумму 2 рядов, по четным и нечетным степеням, получим
.
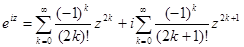Отсюда, учитывая разложение в ряд функций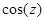 
и 
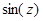, получим представление
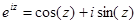(1)
Этой формулой (при вещественном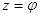 
) мы пользовались еще для представления комплексных чисел в показательной форме, теперь она получила свое обоснование. Подставив в (1) -z вместо z, получим
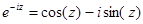(1a)
Взяв полусумму и полуразность формул (1) и (1а), получим
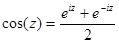, (2)
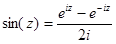. (3)
Формулы (1), (2), (3) носят название формул Эйлера.
В частности, подставив z=ix (где x – вещественное), получим
,
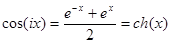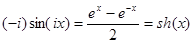.. Вещественные функции вещественной переменной ch(x) и sh(x) называются гиперболическим косинусом и гиперболическим синусом.
Например,
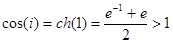
(Вспомните, что я писал на прошлой лекции о возможном нарушении известных неравенств при комплексных значениях переменной.)
Вычисление значений функции.
Фактически мы умеем выполнять над числами только простейшие арифметические операции: сложение, вычитание, умножение (как следствие, возведение в натуральную степень и деление). Разложение функции в степенной ряд позволяет свести вычисление значения этой функции в любой точке из области сходимости получившегося ряда к этим операциям. Действительно, подставив в степенной ряд нужное значение аргумента, получим числовой ряд, сумму которого можно вычислить с любой заданной точностью.
Пример. Вычислить значение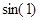 
(естественно, угол выражен в радианах). Используем приведенное в конце прошлой лекции разложение
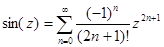
Отсюда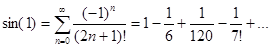 
Получившийся числовой ряд является знакочередующимся с монотонно убывающими членами, поэтому погрешность суммы ряда не превосходит модуля первого отброшенного члена. Таким, образом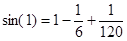 
с погрешностью, не превосходящей 
.
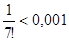Вычисление определенного интеграла.
Вычисление определенного интеграла по формуле Ньютона-Лейбница не получается, если для подынтегральной функции не удается найти первообразную. Если при этом подынтегральную функцию удается представить в виде степенного ряда, сходящегося на интервале интегрирования, то можно воспользоваться правилом интегрирования степенных рядов.
Пусть функция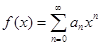 
и интервал (A; B) находится внутри области сходимости этого ряда. Тогда
= 
.
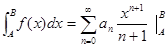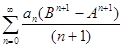Получившийся числовой ряд автоматически является сходящимся. Вычислив его сумму с заданной точностью, получим значение интеграла.
Пример. Вычислить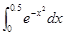 
. Данный интеграл непосредственно не вычисляется, так как первообразная подынтегральной функции не выражается через элементарные функции. Воспользуемся известным рядом для представления функции 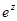и подставим в него в качестве аргумента 
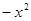. Получим 
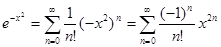. Отсюда находим
= 
= 
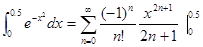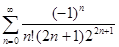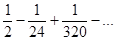
Получившийся ряд – знакочередующийся с монотонно убывающим общим членом и первый не выписанный явно член будет явно меньше по модулю, чем 0.001, поэтому выписанная сумма чисел представляет собой значение интеграла с точностью до 0.001.