Уравнение состояния идеального газа
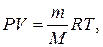
где 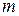 – масса газа;
– масса газа; 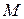 – молярная масса газа;
– молярная масса газа; 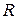 – газовая постоянная;
– газовая постоянная; 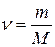 – количество вещества;
– количество вещества; 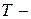 температура.
температура.
Молярная масса смеси газов
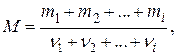
где  – масса
– масса  -го газа, входящего в смесь;
-го газа, входящего в смесь; 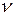 – количество вещества
– количество вещества  -го газа.
-го газа.
Основное уравнение кинетической теории идеальных газов
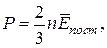
где  – средняя кинетическая энергия поступательного движения молекулы.
– средняя кинетическая энергия поступательного движения молекулы.
Средняя кинетическая энергия, приходящаяся на одну степень свободы молекулы

где  – постоянная Больцмана;
– постоянная Больцмана; 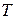 – температура.
– температура.
Полная кинетическая энергия молекулы
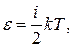
где  – число степеней свободы молекулы.
– число степеней свободы молекулы.
Распределение молекул по скорости (распределение Максвелла)

где 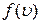 – функция распределения молекул по абсолютным значениям скоростей;
– функция распределения молекул по абсолютным значениям скоростей; 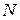 – общее число молекул;
– общее число молекул; 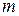 – масса молекулы.
– масса молекулы.
Распределение молекулы по относительным скоростям молекул 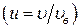
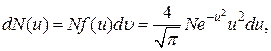
где  – функция распределения молекул по относительным скоростям;
– функция распределения молекул по относительным скоростям;  – наиболее вероятная скорость молекулы.
– наиболее вероятная скорость молекулы.
Средняя квадратичная скорость молекулы
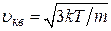 ,
,
где 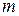 – масса молекулы.
– масса молекулы.
Средняя скорость молекулы
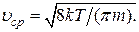
Наиболее вероятная скорость молекулы
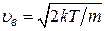 .
.
Барометрическая формула
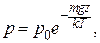
где 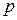 – давление газа;
– давление газа; 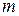 – масса молекулы;
– масса молекулы; 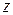 – координата (высота) точки по отношению к уровню, принятому за нулевой;
– координата (высота) точки по отношению к уровню, принятому за нулевой; 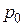 – давление на этом уровне;
– давление на этом уровне;  – ускорение свободного падения;
– ускорение свободного падения;  – постоянная Больцмана.
– постоянная Больцмана.
Распределение молекул в силовом поле (распределение Больцмана)
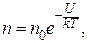
где 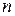 – концентрация молекул;
– концентрация молекул;  – потенциальная энергия молекулы в силовом поле;
– потенциальная энергия молекулы в силовом поле;  – концентрация молекул в точках поля, где
– концентрация молекул в точках поля, где 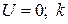 – постоянная Больцмана.
– постоянная Больцмана.
Среднее число столкновений молекулы идеального газа в единицу времени
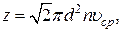
где 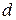 – эффективный диаметр молекулы;
– эффективный диаметр молекулы; 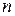 – концентрация молекул;
– концентрация молекул;  – средняя скорость молекулы.
– средняя скорость молекулы.
Средняя длина свободного пробега молекулы
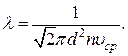
Динамическая вязкость
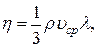
где 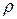 – плотность газа;
– плотность газа;  – средняя длина свободного пробега молекул.
– средняя длина свободного пробега молекул.
Сила внутреннего трения между слоями движущегося газа (жидкости)
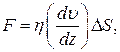
где  – градиент скорости слоев газа (жидкости);
– градиент скорости слоев газа (жидкости); 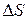 – площадь слоя газа (жидкости).
– площадь слоя газа (жидкости).
Количество теплоты, прошедшее посредством теплопроводности через сечение площадью 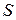 за время
за время 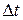 ,
,

где  – теплопроводность;
– теплопроводность; 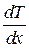 – градиент температуры.
– градиент температуры.
Коэффициент теплопроводности газа
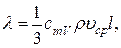
где  – удельная теплоемкость газа при постоянном объеме;
– удельная теплоемкость газа при постоянном объеме; 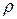 – плотность газа;
– плотность газа;  – средняя скорость молекулы;
– средняя скорость молекулы; 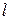 – длина свободного пробега.
– длина свободного пробега.
Масса газа, перенесенная в результате диффузии через поверхность площадью 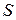 за время
за время 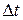 ,
,

где 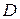 – коэффициент диффузии;
– коэффициент диффузии; 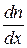 – градиент концентрации молекул;
– градиент концентрации молекул; 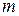 – масса молекулы.
– масса молекулы.
Коэффициент диффузии

| Задание 5.1 | |||
| При увеличении абсолютной температуры идеального газа в 2 раза и концентрации молекул в 4 раза его давление... | |||
| Варианты ответов: | |||
| 1) | увеличилось в 4 раза | 2) | увеличилось в 2 раза |
| 3) | уменьшилось в 2 раза | 4) | увеличилось в 8 раз |
| Задание 5.2 | |||
| При увеличении давления в 3 раза и уменьшении объема в 2 раза абсолютная температура идеального газа... | |||
| Варианты ответов: | |||
| 1) | увеличится в 1,5 раза | 2) | уменьшится в 1,5 раза |
| 3) | увеличится в 6 раз | 4) | уменьшится в 6 раз |
| Задание 5.3 | |||
В баллоне емкостью 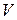 находится некоторый газ массой находится некоторый газ массой 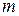 под давлением под давлением 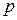 . Средняя квадратичная скорость молекул газа равна... . Средняя квадратичная скорость молекул газа равна...
| |||
| Варианты ответов: | |||
| 1) | 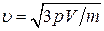
| 2) | 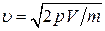
|
| 3) | 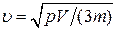
| 4) | 
|
| Задание 5.4 | ||||
На диаграмме 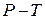 изображен замкнутый процесс в идеальном газе. В каких состояниях, отмеченных цифрами, газ имеет одинаковые объемы? изображен замкнутый процесс в идеальном газе. В каких состояниях, отмеченных цифрами, газ имеет одинаковые объемы?
|
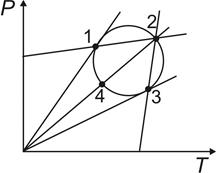
| |||
| Варианты ответов: | ||||
| 1) | 2 и 4 | 2) | 1 и 2 | |
| 3) | 1 и 3 | 4) | 2 и 3 | |
| Задание 5.5 | ||||
На диаграмме  изображен замкнутый процесс в идеальном газе. В каких состояниях, отмеченных цифрами, газ имеет одинаковые давления? изображен замкнутый процесс в идеальном газе. В каких состояниях, отмеченных цифрами, газ имеет одинаковые давления?
|
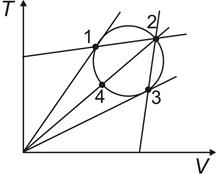
| |||
| Варианты ответов: | ||||
| 1) | 1 и 3 | 2) | 2 и 3 | |
| 3) | 2 и 4 | 4) | 1 и 2 | |
| Задание 5.6 | ||||
На рисунке представлен график распределения молекул идеального газа по скоростям (распределение Максвелла), где  – средняя, – средняя,  – средняя квадратичная скорость молекул газа. С ростом температуры газа отношение – средняя квадратичная скорость молекул газа. С ростом температуры газа отношение  ... ...
|

| |||
| Варианты ответов: | ||||
| 1) | увеличивается | 2) | может как увеличиваться, так и уменьшаться | |
| 3) | не изменяется | 4) | уменьшается | |
| Задание 5.7 | ||||
На рисунке представлен график распределения молекул идеального газа по скоростям (распределение Максвелла). При увеличении температуры газа в 4 раза положение максимума кривой по оси  … …
|
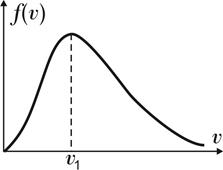
| |||
| Варианты ответов: | ||||
| 1) | не изменится | 2) | сместится в точку 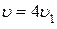
| |
| 3) | сместится в точку 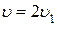
| 4) | сместится в точку 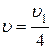
| |
| Задание 5.8 | ||||
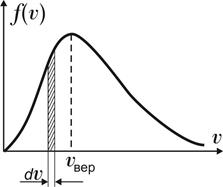
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 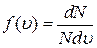 – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от  до до  в расчете на единицу этого интервала. Выберите верные утверждения. в расчете на единицу этого интервала. Выберите верные утверждения.
|
| |||
| Варианты ответов: | ||||
| 1) | С ростом температуры максимум кривой смещается вправо. | 2) | При любом изменении температуры площадь под кривой не изменяется. | |
| 3) | Площадь заштрихованной полоски пропорциональна числу молекул со скоростями в интервале от  до до  . .
| 4) | Площадь заштрихованной полоски пропорциональна доле молекул со скоростями в интервале от  до до  . .
| |
| 5) | При понижении температуры максимум кривой смещается влево. | 6) | При понижении температуры площадь под кривой уменьшается. | |
| 7) | С ростом температуры площадь кривой не изменяется. | 8) | Положение максимума кривой зависит как от температуры, так и от природы газа. | |
| 9) | С ростом температуры площадь под кривой растет. | |||
| Задание 5.9 | ||||
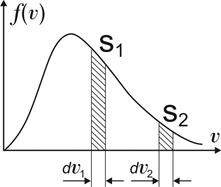
На рисунке представлен график распределения молекул идеального газа по скоростям (распределение Максвелла), где 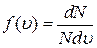 – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от  до до 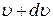 в расчете на единицу этого интервала. Заштрихованная на графике площадь в расчете на единицу этого интервала. Заштрихованная на графике площадь 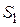 в два раза больше площади в два раза больше площади 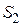 . Это означает, что в интервале скоростей от . Это означает, что в интервале скоростей от  до до 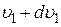 в два раза больше… в два раза больше…
| 
| |||
| Варианты ответов: | ||||
| 1) | для ответа не хватает данных | 2) | количество молекул | |
| 3) | суммарный импульс молекул газа | 4) | суммарная кинетическая энергия молекул | |
| Задание 5.10 | ||||
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 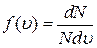 – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от  до до  в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большей молярной массой и таким же числом молекул, то… в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большей молярной массой и таким же числом молекул, то…
| 
| |||
| Варианты ответов: | ||||
| 1) | максимум кривой сместится влево в сторону меньших скоростей | 2) | величина максимума уменьшится | |
| 3) | площадь кривой увеличится | |||
| Задание 5.11 | ||||
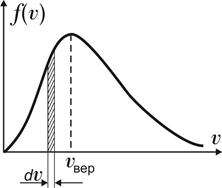
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 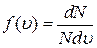 – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от  до до  в расчете на единицу этого интервала. Для этой функции верными утверждениями являются… в расчете на единицу этого интервала. Для этой функции верными утверждениями являются…
| 
| |||
| Варианты ответов: | ||||
| 1) | с ростом температуры площадь под кривой растет | 2) | с ростом температуры величина максимума растет | |
| 3) | с ростом температуры максимум кривой смещается вправо | 4) | с ростом температуры максимум кривой смещается влево | |
| 5) | с ростом температуры площадь заштрихованной полоски будет уменьшаться | 6) | при понижении температуры максимум кривой смещается влево | |
| 7) | при понижении температуры величина максимума уменьшается | 8) | при понижении температуры площадь под кривой уменьшается | |
| Задание 5.12 | ||||
На рисунке представлен график распределения молекул идеального газа по скоростям (распределение Максвелла), где 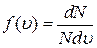 – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от  до до  в расчете на единицу этого интервала. При уменьшении температуры и неизменном интервале скоростей в расчете на единицу этого интервала. При уменьшении температуры и неизменном интервале скоростей  площадь заштрихованной области… площадь заштрихованной области…
|
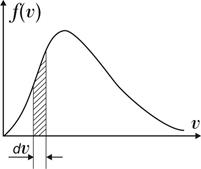
| |||
| Варианты ответов: | ||||
| 1) | не изменяется | 2) | увеличивается | |
| 3) | уменьшается | 4) | может как увеличиться, так и уменьшиться | |
| Задание 5.13 | ||||
На рисунке представлен график распределения молекул идеального газа по скоростям (распределение Максвелла), где 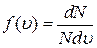 – доля молекул, скорости которых заключены в интервале скоростей от – доля молекул, скорости которых заключены в интервале скоростей от  до до  в расчете на единицу этого интервала. При уменьшении температуры и неизменном интервале скоростей в расчете на единицу этого интервала. При уменьшении температуры и неизменном интервале скоростей  площадь заштрихованной области… площадь заштрихованной области…
|

| |||
| Варианты ответов: | ||||
| 1) | не изменяется | 2) | может как увеличиться, так и уменьшиться | |
| 3) | увеличивается | 4) | уменьшается | |
| Задание 5.14 | ||||
В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота  . Распределение молекул гелия по скоростям описывает кривая… . Распределение молекул гелия по скоростям описывает кривая…
|

| |||
| Варианты ответов: | ||||
| 1) | 2) | |||
| 3) | ||||
| Задание 5.15 | ||||
В трех одинаковых сосудах находится одинаковое количество водорода, причем  . Распределение проекций скоростей молекул водорода на произвольное направление . Распределение проекций скоростей молекул водорода на произвольное направление  в сосуде с температурой в сосуде с температурой  описывает кривая… описывает кривая…
|

| |||
| Варианты ответов: | ||||
| 1) | 2) | |||
| 3) | 4) | |||
| Задание 5.16 | |||
Средняя кинетическая энергия молекул газа при температуре 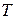 зависит от их структуры, что связано с возможностью различных видов движения молекулы. Средняя кинетическая энергия молекул гелия зависит от их структуры, что связано с возможностью различных видов движения молекулы. Средняя кинетическая энергия молекул гелия 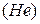 равна... равна...
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 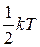
| 4) | 
|
| Задание 5.17 | |||
Средняя кинетическая энергия молекул газа при температуре 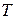 зависит от их структуры, что связано с возможностью различных видов движения молекулы. Средняя кинетическая энергия молекул азота зависит от их структуры, что связано с возможностью различных видов движения молекулы. Средняя кинетическая энергия молекул азота 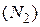 равна... равна...
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 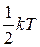
|
| 3) | 
| 4) | 
|
| Задание 5.18 | |||
Средняя кинетическая энергия молекул газа при температуре 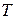 зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, средняя энергия молекул углекислого газа зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, средняя энергия молекул углекислого газа 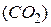 равна... (Учесть, что молекула равна... (Учесть, что молекула 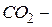 линейная.) линейная.)
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 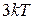
| 4) | 
|
| Задание 5.19 | |||
Средняя кинетическая энергия молекул газа при температуре 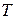 зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, средняя энергия молекул водяного пара зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, средняя энергия молекул водяного пара  равна... равна...
| |||
| Варианты ответов: | |||
| 1) | 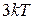
| 2) | 
|
| 3) | 
| 4) | 
|
| Задание 5.20 | |||
Средняя кинетическая энергия молекул газа при температуре 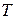 зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, средняя энергия молекул метана зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, средняя энергия молекул метана  равна... равна...
| |||
| Варианты ответов: | |||
| 1) | 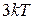
| 2) | 
|
| 3) | 
| 4) | 
|
| Задание 5.21 | |||
Средняя кинетическая энергия молекулы идеального газа при температуре 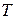 равна равна 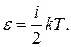 Здесь Здесь  где где 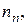  и и 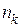 – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, для водорода – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движения молекулы, для водорода  число степеней свободы равно... число степеней свободы равно...
| |||
| Варианты ответов: | |||
| 1) | 2) | ||
| 3) | 4) |
| Задание 5.22 | |||
Максимальное число вращательных степеней свободы для молекулы 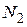 равно... равно...
| |||
| Варианты ответов: | |||
| 1) | 2) | ||
| 3) | 4) |
| Задание 5.23 | |||
Отношение энергии поступательного движения молекулы кислорода 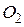 к ее полной внутренней энергии равно... к ее полной внутренней энергии равно...
| |||
| Варианты ответов: | |||
| 1) | 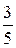
| 2) | 
|
| 3) | 4) | 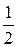
| |
| 5) | 
|
| Задание 5.24 | |||
| Теплоемкость идеального газа при адиабатическом процессе равна... | |||
| Варианты ответов: | |||
| 1) | 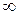
| 2) | 
|
| 3) | 4) | 
|
| Задание 5.25 | |||
Средняя кинетическая энергия молекул газа при температуре 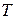 зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место все виды движения молекулы, средняя энергия молекул азота зависит от их структуры, что связано с возможностью различных видов движения молекулы. При условии, что имеют место все виды движения молекулы, средняя энергия молекул азота 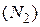 равна... равна...
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 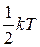
|
| 3) | 
| 4) | 
|
| Задание 5.26 | ||||
На рисунке схематически представлена температурная зависимость молярной теплоемкости при постоянном объеме 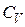 от температуры от температуры 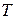 для двухатомного газа. В интервале температур для идеального газа, соответствующих участку для двухатомного газа. В интервале температур для идеального газа, соответствующих участку 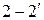 , молекула имеет... , молекула имеет...
|

| |||
| Варианты ответов: | ||||
| 1) | три поступательных, две вращательных и колебательную степени свободы | 2) | три поступательных и две вращательных степени свободы | |
| 3) | три поступательных степени свободы | |||
| Задание 5.27 | ||||
Молярные теплоемкости гелия в процессах 1-2 и 1-3 равны  и и 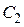 соответственно. Отношение теплоемкостей соответственно. Отношение теплоемкостей 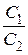 равно... равно...
|

| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 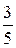
| |
| 3) | 
| 4) | 
| |
| Задание 5.28 | ||||
Молярные теплоемкости двухатомного газа (при условии, что связь атомов в молекуле упругая) в процессах 1-2 и 1-3 равны  и и 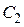 соответственно. Вычислите отношение соответственно. Вычислите отношение 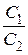 . .
|

| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
Основы термодинамики
Первое начало термодинамики

где  количество теплоты, сообщенное газу;
количество теплоты, сообщенное газу;  приращение его внутренней энергии;
приращение его внутренней энергии; 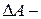 работа, совершаемая газом против внешних сил.
работа, совершаемая газом против внешних сил.
Молярные теплоемкости при постоянном объеме и постоянном давлении
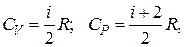
где  – число степеней свободы;
– число степеней свободы; 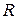 – газовая постоянная.
– газовая постоянная.
Уравнение Майера
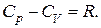
Внутренняя энергия идеального газа

где  – средняя кинетическая энергия молекулы;
– средняя кинетическая энергия молекулы; 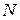 – число молекул газа;
– число молекул газа; 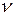 – количество вещества.
– количество вещества.
Работа, связанная с изменением объема газа
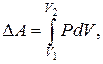
где  – начальный объем газа;
– начальный объем газа; 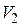 – конечный объем газа.
– конечный объем газа.
Уравнение адиабатического процесса в газе
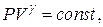
где  – показатель адиабаты.
– показатель адиабаты.
Работа газа при изобарическом процессе 
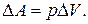
Работа газа при изотермическом процессе 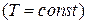
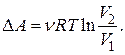
Работа газа при адиабатическом процессе
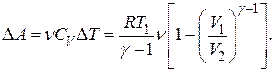
Коэффициент полезного действия цикла

где  – количество теплоты, полученное рабочим телом от нагревателя;
– количество теплоты, полученное рабочим телом от нагревателя;  – количество теплоты, переданное рабочим телом холодильнику.
– количество теплоты, переданное рабочим телом холодильнику.
Коэффициент полезного действия цикла Карно

где 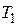 – температура нагревателя;
– температура нагревателя;  – температура холодильника.
– температура холодильника.
Приращение энтропии системы для обратимого процесса
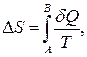
где  и
и  – пределы интегрирования, соответствующие начальному и конечному состоянию системы.
– пределы интегрирования, соответствующие начальному и конечному состоянию системы.
Приращение энтропии идеального газа
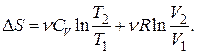
Формула Больцмана
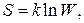
где 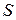 – энтропия системы;
– энтропия системы; 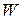 – термодинамическая вероятность состояния системы;
– термодинамическая вероятность состояния системы;  – постоянная Больцмана.
– постоянная Больцмана.
Уравнение Ван-дер-Ваальса
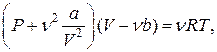
где  и
и 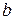 – постоянные Ван-дер-Ваальса;
– постоянные Ван-дер-Ваальса; 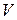 – объем газа;
– объем газа; 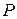 – давление газа.
– давление газа.
Внутренняя энергия реального газа
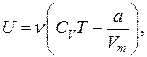
где 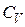 – молярная теплоемкость газа при постоянном объеме;
– молярная теплоемкость газа при постоянном объеме; 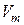 – молярный объем газа;
– молярный объем газа;  – постоянная Ван-дер-Ваальса.
– постоянная Ван-дер-Ваальса.
Поверхностное натяжение
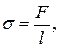
где  – сила поверхностного натяжения;
– сила поверхностного натяжения; 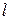 – длина контура, ограничивающего поверхность жидкости.
– длина контура, ограничивающего поверхность жидкости.
Избыточное давление, создаваемое изогнутой поверхностью жидкости (формула Лапласа)

где 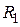 и
и 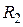 – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
– радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
Высота подъема жидкости в капиллярной трубке
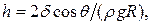
где  – краевой угол,
– краевой угол, 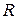 – радиус капилляра,
– радиус капилляра, 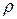 – плотность жидкости,
– плотность жидкости,  – ускорение свободного падения.
– ускорение свободного падения.
Внутренняя энергия одного моля твердого тела, состоящего из одинаковых атомов,
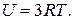
Молярная теплоемкость химически простых твердых тел (закон Дюлонга – Пти)
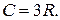
Молярная теплоемкость химически сложных твердых тел (закон Неймана – Конна)

где 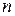 – число частиц в химической формуле соединения.
– число частиц в химической формуле соединения.
| Задание 6.1 | |||
| Если в некотором процессе газ совершил работу, равную 10 кДж, а его внутренняя энергия уменьшилась на 10 кДж, то такой процесс называется... | |||
| Варианты ответов: | |||
| 1) | изотермическим | 2) | адиабатным |
| 3) | изобарным | 4) | изохорным |
| Задание 6.2 | |||
Газ находится в состоянии с параметрами 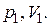 При сжатии газа минимальная работа будет совершена в… При сжатии газа минимальная работа будет совершена в…
| |||
| Варианты ответов: | |||
| 1) | изотермическом процессе | 2) | ни один процесс не подходит |
| 3) | адиабатическом процессе | 4) | изохорическом процессе |
| 5) | изобарическом процессе |
| Задание 6.3 | ||||
Идеальный газ совершает замкнутый цикл 1-2-3-4-1, состоящий из двух изохор и двух изобар. Давление и объем в состоянии 1 равны соответственно 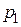 и и  и за цикл изменяются в и за цикл изменяются в 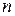 раз. Вычислите работу газа за цикл. раз. Вычислите работу газа за цикл.
|

| |||
| Варианты ответов: | ||||
| 1) | 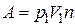
| 2) | 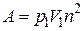
| |
| 3) | 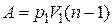
| 4) | 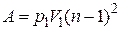
| |
| Задание 6.4 | ||||
На 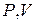 -диаграмме изображен циклический процесс в термодинамической системе. Как изменяется температура системы на участках цикла -диаграмме изображен циклический процесс в термодинамической системе. Как изменяется температура системы на участках цикла  и и  ? ?
|

| |||
| Варианты ответов: | ||||
| 1) | На  понижается, на понижается, на  повышается повышается
| 2) | Повышается | |
| 3) | На  повышается, на повышается, на 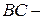 понижается понижается
| 4) | Понижается | |
| Задание 6.5 | |||
Газ находится в состоянии с параметрами 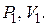 Какой процесс должен произойти в газе, чтобы им была совершена минимальная работа? Какой процесс должен произойти в газе, чтобы им была совершена минимальная работа?
| |||
| Варианты ответов: | |||
| 1) | Изотермический | 2) | Изобарический |
| 3) | Изохорический | 4) | Ни один процесс не подходит |
| 5) | Адиабатический |
| Задание 6.6 | ||||
На 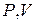 -диаграмме изображены два циклических процесса. Отношение работ, совершенных в каждом цикле, -диаграмме изображены два циклических процесса. Отношение работ, совершенных в каждом цикле, 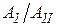 равно... равно...
|
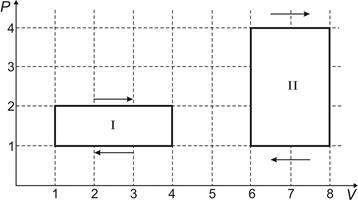
| |||
| Варианты ответов: | ||||
| 1) | -2 | 2) | 1/2 | |
| 3) | 4) | -1/2 | ||
| Задание 6.7 | ||||
| Температура системы от энтропии изменяется так, как показано на графике. Эта зависимость соответствует… |
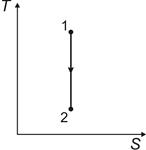
| |||
| Варианты ответов: | ||||
| 1) | адиабатному расширению системы | 2) | изохорному охлаждению системы | |
| 3) | изобарному сжатию системы | 4) | изотермическому сжатию системы | |
| Задание 6.8 | ||||
| Температура системы от энтропии изменяется так, как показано на графике. Эта зависимость соответствует… |
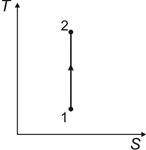
| |||
| Варианты ответов: | ||||
| 1) | адиабатному сжатию | 2) | изохорному нагреванию | |
| 3) | изобарному расширению | 4) | изотермическому расширению | |
| Задание 6.9 | |||
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-03-30 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |