Образовательный минимум.
Модуль 4. Степени и корни.
| Теоретические вопросы |
| 1. Понятие степени с натуральным, целым и дробным показателем. 2. Стандартный вид числа. 3. Свойства степени а) с одинаковым основанием и разным показателем; б) с разным основанием и одинаковым показателем; в) с целым показателем. 4. Квадратный корень. 5. Свойства арифметического квадратного корня. 6. Формула связи степени и корня. |
| Ключевые задачи |
1. Представьте в стандартном виде: а)457; б) 0,0087.
2. Найдите значение выражения: а)  б) (4,9 · 10− 3)(4 · 10− 2).
3. В лабораторию купили электронный микроскоп, который даёт возможность различать объекты размером до б) (4,9 · 10− 3)(4 · 10− 2).
3. В лабораторию купили электронный микроскоп, который даёт возможность различать объекты размером до  Выразите эту величину в миллиметрах. 1) 0,002; 2) 0,0002; 3) 0,00002; 4) 0,000002.
4. Найдите значение выражения: а) Выразите эту величину в миллиметрах. 1) 0,002; 2) 0,0002; 3) 0,00002; 4) 0,000002.
4. Найдите значение выражения: а)  . б) . б)  при при  . в) . в)  при при  ..
5. Найдите значение выражения: а) ..
5. Найдите значение выражения: а)  . б) . б)  6. Найдите значение выражения: а)
6. Найдите значение выражения: а)  ; б) ; б)  ; в) ; в) 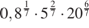 .
7. Какое из следующих выражений равно .
7. Какое из следующих выражений равно  ? В ответе укажите номер правильного варианта.
1) ? В ответе укажите номер правильного варианта.
1)  2) 2)  3) 3)  4) 4)  8. На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу
8. На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу  Какая это точка? Какая это точка?  1) А; 2) В; 3) С; 4) D?
8. Найдите значение выражения: а) 1) А; 2) В; 3) С; 4) D?
8. Найдите значение выражения: а)  б) б)  9. Найдите значение выражения
9. Найдите значение выражения  10. Найдите значение выражения: а)
10. Найдите значение выражения: а)  при при  . б) . б)  .
11. Найдите значение выражения: а) .
11. Найдите значение выражения: а)  б) (1 – б) (1 –  )( )( + 1).
12. Значение какого из выражений является числом иррациональным?
1) + 1).
12. Значение какого из выражений является числом иррациональным?
1)  2) 2)  3) 3) 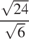 4) 4) 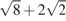
|
Определение: а · а · … · а = аn, а1 = а, а0 = 1, где n  N, n> 1. N, n> 1.
 n –раз
Если n и m рациональные числа, то справедливы следующие свойства:
n –раз
Если n и m рациональные числа, то справедливы следующие свойства:
| |||
| an · am = an + m |  , a ≠ 0 , a ≠ 0
| ||
| an:am = an-m | |||
| (an)m = an·m | |||
| an· bn = (a·b)n |  , a,b ≠ 0 , a,b ≠ 0
| ||
 = =  , b ≠ 0 , b ≠ 0
|
Стандартныйвидчисла. Каждое число больше 10, можно записать в виде а·10n, где 10 ≥ а ≥ 1.
|
|
Пр. 457 = 4,57·102; 0,0087 = 8,7  10-3.
10-3.
Задание
9. Найдите значение выражения 
10. Найдите значение выражения 
11. Найдите значение выражения 
12. Найдите значение выражения (4,9 · 10− 3)(4 · 10− 2).
5. Площадь территории России составляет 1,7 · 107 км2, а Норвегии — 3,2⋅105 км2. Во сколько раз площадьтерритории России больше площади территории Норвегии? В ответе укажите номер правильного варианта.
1) примерно в 1,9 раза; 2) примерно в 5,3 раза;3) примерно в 53 раза; 4) примерно в 530 раз.
6. В лабораторию купили электронный микроскоп, который даёт возможность различать объекты размером до 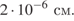 Выразите эту величину в миллиметрах. В ответе укажите номер правильного варианта.
Выразите эту величину в миллиметрах. В ответе укажите номер правильного варианта.
1) 0,002 2) 0,00023) 0,000024) 0,000002
7. Найдите значение выражения 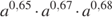 при
при  .
.
8. Найдите значение выражения  при
при  .
.
9. Представьте выражение  в виде степени с основанием x.
в виде степени с основанием x.
10. Найдите значение выражения  при
при  .
.
11. Найдите значение выражения 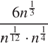 при
при  .
.
12. Представьте выражение  в виде степени с основанием c.
в виде степени с основанием c.
13. Представьте выражение  в виде степени с основанием
в виде степени с основанием 
14. Найдите значение выражения  при
при  .
.
15. Найдите значение выражения  при
при  .
.
16. Найдите значение выражения  .
.
17. Найдите значение выражения  .
.
18. Найдите значение выражения  .
.
19. Найдите значение выражения  .
.
|
|
20. Найдите значение выражения  .
.
21. Найдите значение выражения  при
при  .
.
22. Найдите значение выражения  .
.
23. Найдите значение выражения  .
.
25. Найдите значение выражения  .
.
26. Найдите значение выражения  .
.
27. Найдите значение выражения 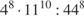 .
.
28. Найдите значение выражения  .
.
29. Найдите значение выражения  .
.
30. Какое из следующих выражений равно  ? В ответе укажите номер правильного вариаyта.
? В ответе укажите номер правильного вариаyта.
1)  2)
2) 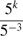 3)
3)  4)
4) 
31. Какое из следующих выражений равно 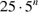 ? В ответе укажите номер правильного варианта.
? В ответе укажите номер правильного варианта.
1)  2)
2)  3)
3)  4)
4) 
____________________________________________
Доп.
А) Найдите значение выражения  при
при  .
.
Б) Найдите значение выражения  при
при  .
.
В) Упростите выражение:  .
.
Г) Упростите выражение:  .
.
Д) Сократите дробь 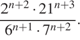
Е) Сократите дробь 
Ж) Сократите дробь  .
.
З) Найдите значение выражения  , если
, если  .
.
Корень n-й степени
Обозначение: 
Корнем n-й степени из числа а называется такое число b, n-я степень которого равна а, то есть 
1) Если n - нечетное число, то существует единственный корень n-й степени из любого числа (положительного или отрицательного). Например, 
2) Если n - четное число, то существует два корня n-й степени из любого положительного числа. Например, корень четвертой степени из числа 625 - это числа -5 и 5. Так как 
Корень четной степени из отрицательного числа не существует! Например, 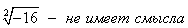 ,
,
Арифметический корень n-й степени
Это то же самое, что и корень n-й степени, но разница в том, что арифметический корень из неотрицательного числа есть неотрицательное число!
|
|
То есть, если n - четное число, то существует один положительный корень n-й степени из любого положительного числа.

Замечания:
1) если a> 0, то  = a и
= a и  ;
;
2) если a - любое, и n- чётное число, то  , в частности:
, в частности: 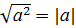
Пример: а)  = |4|; б)
= |4|; б)  .
.
3) если a- любое и n - нечётное число, то 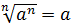 .
.
Пример:  для любого значения х,
для любого значения х,  .
.