Перестановки и подстановки.

Глава 3. Определители n-го порядка.

В настоящей главе понятие определитель обобщается максимально: будем считать порядок 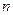определителя произвольным. Изучая определители 2-го и 3-го порядков, всё время имелась в виду целевая задача: решение системы линейных уравнений. Потом были обнаружены дополнительные возможности определителей в приложениях к задачам геометрии и физики. Так как для числа измерений больше трёх мы не можем представить себе реальных геометрических образов, то будем считать целью развития понятия определитель – решение систем линейных уравнений с 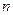неизвестными: x ₁, x ₂, …, .

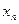При переходе от определителя 2-го порядка к определителю 3-го порядка использовалось соответствие:

квадратная матрица: A = 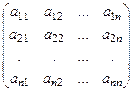→ определитель: 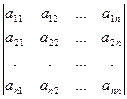=| A |= d,

причём каждый член определителя должен формироваться по правилу: это произведение 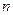элементов 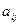определителя, взятых по одному из каждой строки и каждого столбца:

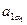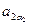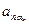· ·…· – общий член определителя.

Число членов определителя: определяется перестановкой = n! Остаётся определить знак каждого члена определителя.

Очевидно, поиск геометрических схем определения знака члена определителя – бесперспективен! Нужно искать совсем другие схемы решения этой задачи. А значит, задачи вычисления определителя 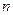- го порядка!

Перестановки и подстановки.

Рассмотрим множество М целых чисел: 1,2,…, n. Элементы множества М можно распо­ложить разными способами.

Определение: (3.1)

всякое расположение чисел 1,2,…, n в некотором порядке называется переста­новкой из n чисел. Общий вид записи перестановки из n элементов: 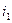, ,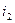…, , 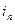(1) где каждое 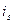есть одно из чисел 1,2,…, n, причем ни одно из этих чисел не встре­чается дважды и не пропущено.

В качестве 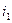можно выбрать любое из чисел 1, 2, …, n. Это дает n различных возможно­стей. Если 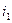уже выбрано, то в качестве 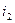можно выбрать лишь одно из оставшихся (n -1) чи­сел, т.е. различных способов выбрать числа (символы) 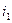и 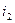равно произведению n∙ (n -1) и т.д. Число перестановок из n символов равно произведению:

Если в некоторой перестановке поменяем местами какие-либо два символа, не обяза­тельно стоящие рядом, а все остальные оставим на месте, то получим новую перестановку. Та­кое преобразование перестановки называется транспозицией.

Теорема: (3.1)

Все перестановки из n символов можно расположить в таком порядке, что каж­дая следующая перестановка получается из предыдущей одной транспозицией, причем начинать можно с любой перестановки.

► Доказательство проведем методом математической индукции. При n =2 утверждение справедливо: 1) так как: 2! = 1·2 = 2, то всего перестановок 2;

2) пусть 1-я перестановка: 1, 2 → тогда 2-я: 2, 1;

3) пусть 1-я перестановка: 2, 1 → тогда 2-я: 1, 2.

Пусть для (n -1) символов теорема выполняется. Рассмотрим все перестановки из n эле­ментов, у которых на первом месте стоит символ 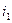(не перемещается!). Таких перестановок (n -1)! и их можно (в соответствии с предположением) упорядочить так, как требует теорема. Пусть последняя из таких перестановок имеет вид:

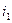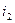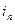, ,…, , (2)

В перестановке (2), содержащей n символов, совершим транспозицию символа 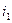с лю­бым другим (например, с символом 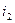) и вновь упорядочим все перестановки из (n -1) символов при фиксированном на первом месте 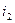и т.д. Так поступим n раз. Это обеспечит пе­ребор всех n! перестановок для n символов. ◄

Следствие: от любой перестановки из n символов можно перейти к любой другой переста­новке из тех же символов при помощи нескольких транспозицией.

Если в перестановке символ 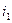стоит раньше, чем символ 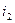, но 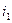> 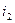, то говорят, что символы 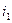и 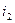составляют инверсию (нарушение порядка), иначе указанные символы составляют порядок. Перестановка называется чётной, если ее символы составляют чётное число инверсий, и нечётной – в противном случае.

Теорема: (3.2)

Всякая транспозиция меняет чётность перестановки.

► Пусть транспонируются символы: ☺ и ☻. Отметим символом ♦ те символы перестановки, которые транспозицией не затрагиваются. Рассмотрим два возможных случая:

1) перестановки имеет вид: ♦♦♦♦ ☺☻ ♦♦♦♦♦ и символы ☺ и ☻ не составляют инверсию; к выделенным символам применим одну транспозицию: ♦♦♦♦ ☻☺ ♦♦♦♦♦ → теперь сим­волы ☻ и ☺ составляют инверсию.

2) пусть перестановка записана в виде:

♦

♦

♦

☺

a1

a2

...

ak

☻

♦

♦

♦

♦

Транспозиций

...

k+1

♦

♦

♦

☻

☺

a1

...

ak-1

ak

♦

♦

♦

♦

...

k

♦

♦

♦

☻

a1

a2

...

ak

☺

♦

♦

♦

♦

В исходном положении символы ☺ и ☻ разделяют некоторые k символов. Если бы мы решили сразу поменять местами выделенные элементы, то не смогли бы оценить изменение их взаимоотношений с разделяющими их элементами! Поэтому берём элемент ☻, и, обмениваясь местами только с соседним левым элементом, движемся влево... На последнем шаге меняются местами выделенные элементы. Теперь имеем рядом элементы: ☻ и ☺. На такое преобразование потребовалось (k+1) транспозиций.

Для того, чтобы элемент ☺ переместился на исходное место элемента ☻, ему потребуется k транспозиций. Итак, мы обеспечили выделенным элементам транспозицию, применив 2k+1 легко учитываемых транспозиций. Так как число 2k+1 есть нечётное число, то это значит: если символы ☺ и ☻ не составляли инверсию, теперь составляют. И наоборот! ◄

Теорема: (3.3)

Сумма порядков и инверсий постоянна и равна: N = .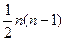

► Пусть исходная запись перестановки ☺: 1, 2, …, n; нарушений порядка нет. Запишем те­перь перестановку в виде ☻: n, (n-1), …, 2, 1; теперь нарушений порядка наибольшее число. От перестановки ☺ к перестановке ☻ можно перейти, используя минимальное число транспозицией: N = 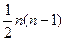. Этот результат легко прочитывается из схемы, использованной при доказательстве теоремы 3.2. ◄

Анализируя рассмотренные свойства перестановок, замечаем: для формирования индексов одного из множителей общего члена определителя: 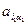· ·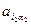…· 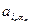требуется совместное использование двух перестановок: 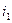, ,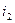..., 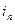и 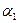, ,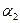..., . 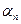При этом: 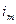указывает номер строки, а 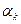номер столбца, выбираемых для выделенного множителя члена определителя. Заметим также, что для определителя удобно последовательность 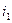, ,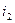..., 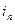заменить последовательностью: 1,2,..., n, так как в этом случае при выборе строк совсем не нужно тратить время на размышления!

Отражая выявленную потребность определителей, стали изучать специальные алгебраические конструкции – подстановки, причём исходное их определение использует две совершенно равноправные перестановки.

Определение: (3.2)

Запишем одну перестановку под другой: 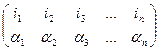. Эту запись назы­вают подстановкой.

Под подстановкой понимают отображение (соответствие) множества символов, состоящего из первых n чисел: 1, 2, …, n, на себя: .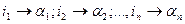

Рассмотрим пример подстановки, используя две произвольные перестановки, содержащие одни и те же элементы. .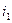

☺☺

Пример 3 – 01: Пусть записана подстановка: 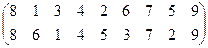. Что это значит?

Ответ: задано преобразование элементов (чисел) множества 1,2, …, n само на себя, а именно: 1 → 6; 2 → 5; 3 → 1; 4 → 4; 5 → 2; 6 → 3; 7 → 7; 8 → 8; 9 → 9.

☻

Из примера видим, что подстановка как отображение множества чисел 1, 2, …, n не ме­няется при транспозиции столбцов. Для приложений, ради которых мы вводим подстановки, не важен порядок столбцов подстановки. Всегда будем предполагать эквивалентность подстановок:

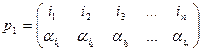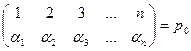→ , (3)

где 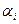– число, в которое переходит число .

☺☺

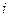Пример 3 – 02: Почему запис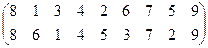и: и 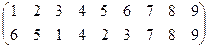– эквивалентны?

Ответ: обе подстановки определяют одно и то же преобразование элементов (чисел) множества 1,2, …, n само на себя, а именно: 1 → 6; 2 → 5; 3 → 1; 4 → 4; 5 → 2; 6 → 3; 7 → 7; 8 → 8; 9 → 9.

☻

Из определения эквивалентности подстановок следует, что подстановки порядка 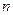различаются только нижней перестановкой элементов. Как было показано при рассмотрении элементов комбинаторики, число различных перестановок = !

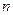Для подстановок вводят понятия: чётная подстановка и нечётная:

▫ для записи подстановки :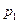

- подстановка чётная, если четности верхней и нижней перестановок совпадают;

- подстановка нечётная, если четности её верхней и нижней перестановок противоположны.

▫ для записи подстановки :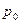

- подстановка чётная, если ее определяет четная перестановка нижней строки;

- подстановка нечётная, если ее определяет нечетная перестановка нижней строки.

☺☺

Пример 3 – 03: Определим чётность заданной подстановки: .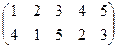

Решение:

Четность подстановки определяется числом инверсий в нижней ее строке (перестановке). Для подсчета числа инверсий перестановки воспользуемся таблицей, в которой:

- символом ☻ отмечается исследуемый элемент;

- символом ♦ отмечается элемент, по отношению к которому исследуемый элемент нарушает порядок: составляет инверсию.

Видим: общее число инверсий нижней перестановки равно 5.
☻	♦		♦	♦	=3
	☻				=0
		☻	♦	♦	=2
			☻		=0
Число инверсий:	=5

Так как число 5 нечетное, то нижняя перестановка, значит и подстановка, нечетная.

☻

Кроме подсчета числа инверсий в перестановках для определения четности подстановок применяют также разложение их в циклы. Воспользуемся этим приемом (не обосновывая его, примем на веру!), рассмотрев конкретный пример.

☺☺

Пример 3 – 03: Определим чётность подстановки 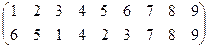, используя разложение её в произведение циклов.

Решение:

Для иллюстрации правила формирования произвольных циклов покажем один из них, начинающийся с первого элемента верхней строки подстановки:

	●		●	●		●	●	●	●
	●		●	●		●	●	●	●

На этой схеме из последовательности выделен один цикл: (1 → 6 → 3 → 1). Запись цикла в разложении подстановки записывают в виде: (1,6,3), не повторяя второй раз элемент начала цикла.

Полное разложение подстановки в произведение циклов для рассматриваемого примера принимает вид: = ,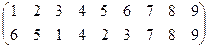

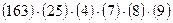где остающиеся на месте элементы отмечены скобками: (4), (7), (8), (9).

Имея разложение подстановки в циклы, определим число декремент: d = n – s, где n – порядок подстановки, s – число циклов в разложении подстановки. В рассматриваемом примере: d = 9 – 6 = 3 – нечетное число → подстановка нечетная.

Ответ: подстановка четная.

Пример 3 – 04: Имеется запись подстановки в циклах: , найти запись этой подстановки в выражении с двумя перестановками.

Решение:

Используя правила построения циклов подстановки:

1) Запишем верхнюю строку подстановки: (1 2 3 4 5).

2) Отразим в нижней строке подстановки каждый из циклов:

▫ цикл: (1 3) → (1 → 3 → 1) → (3 ● 1 ● ●);

▫ цикл: (2 5) → (2 → 5 → 2) → (● 5 ● ● 2);

▫ цикл: (4) → (4 → 4) → (● ● ● 4 ●).

2) Подстановка принимает вид: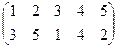

Ответ: .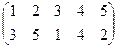

☻

Наблюдения: 1) Как только записан один из членов определителя: 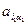· ·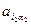…· 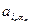, можно записать однозначно определяемую им подстановку.

2) При выборе члена определителя однозначно определяется чётность подстановки → вопрос: А не зависит ли знак члена определителя от чётности подстановки?

Проверим гипотезу на примере определителя 3-го порядка, используя схему его вычисления в соответствии с определением:

= + + – – – ,

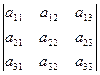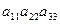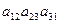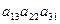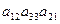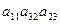Схема проверки гипотезы:

▫ для каждого члена определителя записываем соответствующую подстановку;

▫ вычисляем чётность подстановки;

▫ сопоставляем чётность-нечётность подстановки со знаками 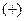- 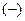выделенного члена определителя.

A¹: 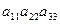→ 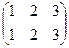: число инверсий в подстановке =0 → подстановка чётная → .

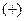A²: 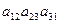→ : число инверсий в подстановке =2 → подстановка чётная → .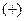

A³: → 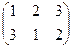: число инверсий в подстановке =2 → подстановка чётная → .

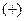A⁴: 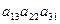→ 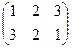: число инверсий в подстановке =3 → подстановка нечётная → .

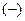A⁵: 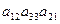→ 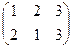: число инверсий в подстановке =1 → подстановка нечётная → .

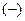A⁶: 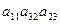→ 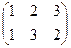: число инверсий в подстановке =1 → подстановка нечётная → .

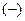Выводы: 1) Знак члена определителя и чётность соответствующей ему подстановки взаимно однозначно соответствуют друг другу.

2) Членов определителя 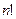, столько же подстановок.

3) Среди членов определителя: отрицательных членов столько же, сколько положительных; среди подстановок нечётных столько же, сколько чётных.

§ 2. Определители n-го порядка .

То, как и какими средствами была решена задача определения знака члена определителя, должно вызывать изумление и восторг у всех, кто знакомится с этим решением! Восторг наблюдать и понимать одухотворенность интеллекта homo sapiens!

Соответствие знака члена определителя и чётности соответствующей ему подстановки распространяем на определители 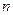- го порядка!

Итак, в результате обобщений всех знаний из теории определителей 2-го и 3-го порядков получено стройное и строгое определение определителя 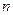- го порядка:

1⁰: квадратная матрица: A = 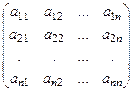→ определитель: 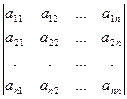=| A |= d.

2⁰: записываем сумму n! членов определителя со знаками, определяемыми подстановками: важно не пропустить ни одного члена определителя!..

Сочувствие: если вы хотите посчитать определитель 9-го порядка (всего-то!), вам нужно записать, строка за строкой, 9! = 362880 членов определителя, каждый из которых составлен из девяти сомножителей.

☺☺

Пример 3 – 05: Выяснить, входит или нет в определитель данное произведение: 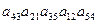. Если указанное произведение входит в определитель, то с каким знаком?

Решение:

1) Для наглядности составим подстановку: 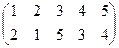. Видим, что в качестве множителей в произведении участвуют элементы определителя, взятые по одному из всех строк и столбцов. Вывод: заданное произведение входит в определитель.

2) Так как 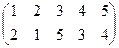= 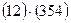, то декремент: 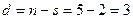– нечетное число → подстановка нечетная → знак минус.

Ответ: входит со знаком минус.

☻

Для решения проблемы вычисления определителя 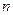-го порядка необходимо установить свойства определителя 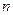-го порядка, подобные тем, что мы получили для определителей 2-го и 3-го порядков. Основная цель: определить правила сведения вычисления определителя 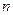-го порядка к вычислению определителя 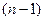–го порядка!

Свойство 1. Величина определителя не изменится, если строки и столбцы этого определителя поменять ролями, для матрицы это преобразование называется транспонированием:

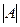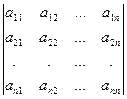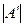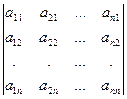= → = . (4)

► Выделим в исходном определителе 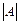некоторый член этого определителя:

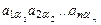. (5)

Для определения знака выделенного члена определителя составим подстановку n -го порядка:

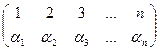, (6)

в ней верхняя перестановка отражает номера строк определителя, в которых размещены эле­менты матрицы, входящие в выражение (5); а нижняя – номера столбцов.

После транспонирования матрицы A те же элементы будут участвовать в выражении члена определителя матрицы :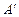

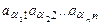, (7)

причем для определения знака, который будет иметь этот член в определителе 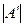должна использоваться подстановка:

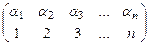. (8)

Очевидно, четности подстановок (6) и (8) совпадают (используем определение четности подста­новки).

Нами доказано одно из важнейших свойств определителя n -го порядка (теперь уже для всех n = 2, 3, …): Определитель не меняется при транспонировании матрицы: 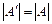. Это свойство устанавливает равноправие строк и столбцов определителя. ◄

Свойство 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю:

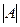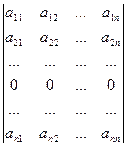= =0. (9)

► Пусть в определителе 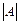строка с номером k вся состоит из 0. Это значит, что общий член определителя обязательно (не пропускается ни одна строка) будет содержать 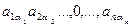0:

=0,

а это значит, что все члены определителя равны 0. ◄

Свойство 3. Если в определителе переставлены две строки (столбца), то все члены полученного определителя те же, что и в исходном определителе, но с обратным знаком, т.е. перестановка двух строк определителя меняет его знак.

► Следует из представленной ниже схемы преобразования определителя и соответствующих подстановок.

●

●

●

●

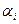
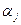
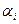
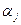
i

●

☺

●

●

●

●

●

●

●

☻

●

●

i

●

●

●

●

j

●

●

●

☻

●

●

●

☺

●

●

●

●

j

●

●

●

●

●

●

●

●

, .

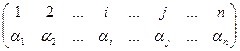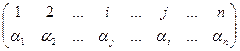видим: четности соответствующих подстановок поменялись! ◄

Свойство 4. Определитель, имеющий две одинаковые строки, равен нулю.

► При перестановке этих строк из свойства 3 следует, что d = –d, т.е. d = 0. ◄

Свойство 5. Если все элементы строки - 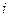определителя умножить на произвольное число k, то определитель умножается на число k.

► Следует из записи общего члена определителя: каждый член определителя содержит ровно один элемент из строки - 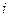, поэтому всякий из них приобретает множитель k, то есть сам определитель умножается на k. ◄

Свойство 6. Определитель, содержащий две пропорциональные строки, равен нулю.

► Следует из свойств 5 и 4. ◄

Свойство 7. Если все элементы строки - 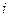определителя имеют вид: 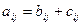, где j = 1, 2, …, n, то определитель равен сумме двух определителей, у которых все строки, кроме строки - 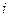, такие же, как в заданном определителе, а строки - 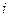в одном из определи­телей состоит из элементов 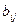, а в другом – из элементов .

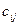► Следует из определения общего члена определителя: выражение (6):

= + .

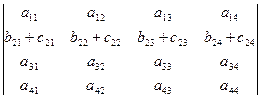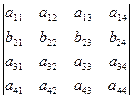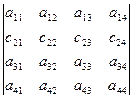Свойство важное при доказательствах дальнейших свойств! ◄

Свойство 8. Если одна из строк определителя есть линейная комбинация других его строк, то оп­ределитель равен нулю.

► Следует из последовательного применения свойств 7, 6, 5, 4). ◄

Свойство 9. Определитель не меняется, если к элементам одной из его строк прибавляются соот­ветствующие элементы другой, умноженной на одно и то же число.

► Следует из свойств 7 и 6. Обобщение: определитель не меняется, если к одной из его строк прибавляется линейная комбинация других его строк. ◄

Рассмотренные (и доказанные!) свойства определителя n -го порядка подготовили сред­ства, необходимые для решения проблемы размерности: не выписывать его n! членов и не определять их знаки.

☻ Если не ставить требование наработки разнообразных навыков рационального вычисления определителей, то, используя определение и свойства определителей, своевременно задать вопрос: введённое понятие определителя обеспечивает решение системы линейных уравнений для произвольного числа неизвестных ?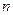

Итак, перейдём от формальной конструкции определителя 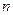-го порядка и его формальных свойств к конкретным приложениям. Пусть имеем систему 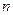линейных уравнений с неизвестными _, :

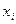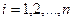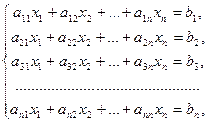
где коэффициенты 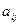, 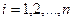; ; 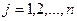при неизвестных 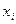_; свободные члены 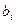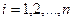_, , хотя бы одно из которых не равно нулю, считаются заданными.

Системе уравнений соответствуют: матрица системы A (составлена из коэффициентов при неизвестных) и расширенная матрица 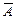(составлена из всех ее коэффициентов, включая свободные члены): , .

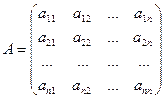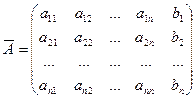Используя свойства определителей 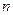-го порядка, преобразуем систему уравнений так, чтобы было выделено уравнение, в которое входит только одна неизвестная переменная 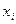. Для этого умножим 1-е уравнение на алгебраическое дополнение 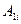, 2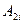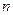-е на ,…, -е на 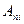. Учитывая разложение определителя по столбцу- 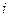, получаем:

= → ,

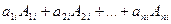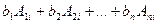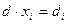где: d = , = .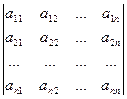

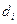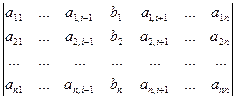Если 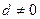, то получаем формулы Крамера: 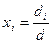– решение заданной системы уравнений.

Замечания: 1) показано решение системы уравнений только для частного случая системы: число уравнений равно числу неизвестных и хотя бы одно 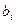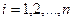_, не равно нулю;

2) для нас важным было показать, что определение определителя обеспечивает решение системы линейных уравнений, и мы в этом убедились;

3) для анализа и решения произвольных систем линейных уравнений потребуется ещё много дополнительных сведений, которые размещены в следующих главах.

Так как использование определителей не ограничивается их применением для решения систем линейных уравнений, то изучение дополнительных способов их эффективного вычисления целесообразно для дальнейших применений: при изучении линейных векторных пространств, алгебры матриц, линейных операторов, квадратичных форм и других.

При рассмотрении определителей 2-го и 3-го порядков введено понятие миноров 1-го порядка. Определитель 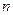-го порядка позволяет выделять миноры большего порядка: реализация принципа обобщений. Посмотрим, насколько это окажется продуктивным!

Пусть имеем определитель n -го порядка. Для целого числа 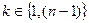выбираем в определителе k строк и k столбцов и зачёркиваем их. Элементы, стоящие на пересечении этих строк и столбцов, образуют матрицу порядка k. Определитель этой матрицы называется минором M k-го порядка определителя d. Элементы, оставшиеся не зачёркнутыми, располагаются в не зачёркнутых (n - k) строках и (n - k) столбцах, образуют минор M′ (n-k) -го порядка, который называют дополнительным минором для минора M. Наоборот, можно вычеркнуть (n-k) строк и (n - k) столбцов – останется минор k -го порядка. Ниже приведена схема выделения минора k -го порядка вычеркиванием k строк и k столбцов:

j 1

j 2

j 3

j 1

j 2

j 3

●

●

●

●

●

●

●

●

☻

☻

☻

●

●

●

●

●

i 1

i 1

●

☻

●

☻

●

☻

●

●

☻

☻

☻

●

●

●

●

●

i 2

●

●

●

●

●

●

●

●

☻

☻

☻

●

●

●

●

●

i 3

●

●

●

●

●

●

●

●

→

●

●

●

●

●

●

●

●

i 2

●

☻

●

☻

●

☻

●

●

●

●

●

●

●

●

●

●

i 3

●

☻

●

☻

●

☻

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●

●